Middelmatig verschil

Von Dr.benjamin anderson August 5, 2023 Statistieken Keine Kommentare

In dit artikel wordt uitgelegd wat de gemiddelde afwijking is en hoe deze wordt berekend. Ook vindt u concrete voorbeelden van het berekenen van de gemiddelde afwijking. En bovendien kunt u de gemiddelde afwijking van elke statistische gegevensset berekenen met behulp van een online rekenmachine.

Wat is gemiddelde afwijking?

Gemiddelde afwijking , ook wel gemiddelde absolute afwijking genoemd, is een maatstaf voor statistische spreiding.

De gemiddelde afwijking van een dataset is het gemiddelde van de absolute afwijkingen . Daarom is de gemiddelde afwijking gelijk aan de som van de afwijkingen van elk gegevensitem van het rekenkundig gemiddelde gedeeld door het totale aantal gegevensitems.

Met andere woorden, de formule voor de gemiddelde afwijking is als volgt:

👉 U kunt de onderstaande rekenmachine gebruiken om de gemiddelde afwijking van elke dataset te berekenen.

In de statistiek wordt de gemiddelde afwijking ook wel de gemiddelde absolute afwijking genoemd.

De interpretatie van de gemiddelde afwijking gebeurt als volgt: hoe groter de waarde van de gemiddelde afwijking, dit betekent dat de gegevens gemiddeld verder van het rekenkundig gemiddelde verwijderd zijn; omgekeerd: hoe lager de gemiddelde afwijking, hoe dichter de waarde. de gegevens zijn. De gemiddelde afwijking geeft dus de spreiding van een datareeks aan.

Andere maten die als gedistribueerd worden beschouwd, zijn bereik, interkwartielbereik, standaardafwijking (of standaardafwijking), variantie en variatiecoëfficiënt.

Hoe de gemiddelde afwijking te berekenen

Om de gemiddelde afwijking van een gegevensreeks te berekenen, moeten de volgende stappen worden gevolgd:

Bereken het rekenkundig gemiddelde van de statistische gegevensset.
Bereken de afwijking van elk gegevenspunt van het gemiddelde, gedefinieerd als de absolute waarde van het verschil tussen de gegevens en het gemiddelde.
Tel alle verschillen op die in de vorige stap zijn berekend.
Deel door het totale aantal gegevens. Het verkregen resultaat is de gemiddelde afwijking van de gegevensreeks.

Samenvattend is de formule die moet worden toegepast om de gemiddelde afwijking te vinden:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|}{N}$

Voorbeeld van het berekenen van de gemiddelde afwijking

Gezien de definitie van gemiddelde afwijking, vindt u hieronder een stapsgewijs opgelost voorbeeld van het berekenen van de gemiddelde afwijking van een statistische steekproef. Op deze manier begrijpt u beter hoe u de gemiddelde afwijking kunt bepalen.

Een analist bestudeert de economische resultaten van een bedrijf over het afgelopen jaar en beschikt over informatie over de winst die het bedrijf gedurende elk kwartaal van dat jaar heeft behaald: 2, 3, 7 en 5 miljoen dollar. Wat is de gemiddelde afwijking van de gegevens?

Eerst moeten we de gegevens middelen, dus tellen we op en delen we door het totale aantal waarnemingen (4):

$\overline{x}=\cfrac{2+3+7+5}{4}=4,25$

Nadat we het rekenkundig gemiddelde hebben berekend, gebruiken we de formule voor de gemiddelde afwijking:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|}{N}$

We vervangen de gegevens in de formule:

$D_{\overline{x}}=\cfrac{|2-4,25|+|3-4,25|+|7-4,25|+|5-4,25|}{4}$

We voeren de berekeningen uit in de teller:

$D_{\overline{x}}=\cfrac{|-2,25|+|-1,25|+|2,75|+|0,75|}{4}$

$D_{\overline{x}}=\cfrac{2,25+1,25+2,75+0,75}{4}$

$D_{\overline{x}}=\cfrac{7}{4}$

En ten slotte delen we door het totale aantal gegevens om de gemiddelde afwijking van het monster te verkrijgen:

$D_{\overline{x}}=1,75$

Berekening van gemiddelde afwijking

Voer een reeks statistische gegevens in de volgende rekenmachine in om de gemiddelde afwijking ervan te berekenen. Gegevens moeten worden gescheiden door een spatie en moeten worden ingevoerd met de punt als decimaal scheidingsteken.

Gemiddelde afwijking voor gegroepeerde gegevens

Om de gemiddelde afwijking van gegevens gegroepeerd in intervallen te berekenen, moeten de volgende stappen worden gevolgd:

Bepaal het rekenkundig gemiddelde van de statistische gegevensset. Omdat de gegevens gegroepeerd zijn, is de uitdrukking om het gemiddelde te berekenen:

$\overline{x}=\cfrac{\sum_{i=1}^N x_i\cdot f_i}{N}$

Bereken de afwijking van elk interval van het gemiddelde, wat gelijk is aan de absolute waarde van het verschil tussen het klascijfer en het gemiddelde.

$|x_i-\overline{x}|$

Vermenigvuldig de afwijking van elk interval met de absolute frequentie.

$|x_i-\overline{x}|\cdot f_i$

Tel alle resultaten van de vorige stap bij elkaar op en deel deze vervolgens door het totale aantal gegevens. Het verkregen resultaat is de gemiddelde afwijking van het monster, gegroepeerd in intervallen.

$\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}$

Concluderend is de formule voor het verkrijgen van de gemiddelde afwijking van gegroepeerde gegevens :

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}$

Wanneer gegevens worden gegroepeerd, betekent dit meestal dat er veel gegevens zijn en dat het vinden van de gemiddelde afwijking veel stappen omvat. Daarom worden meestal frequentietabellen gebruikt om de berekening uit te voeren.

Hieronder vindt u een stapsgewijze oefening over het berekenen van de gemiddelde afwijking wanneer gegevens in intervallen zijn gegroepeerd:

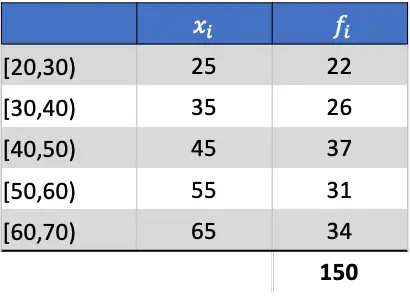
Het eerste dat u moet doen, is het gemiddelde van de gegroepeerde gegevens berekenen. Om dit te doen, voegen we een kolom aan de tabel toe door de klassenoot te vermenigvuldigen met de frequentie ervan:

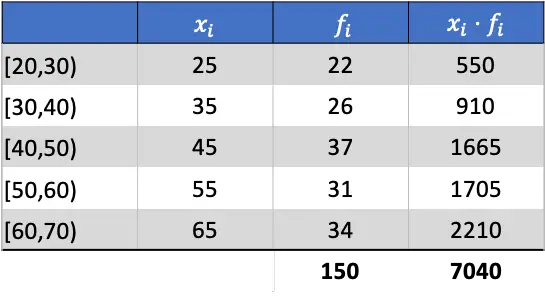
Het rekenkundig gemiddelde zal daarom het resultaat zijn van het delen van de som van de toegevoegde kolom door de som van de absolute frequenties:

$\overline{x}=\cfrac{\sum_{i=1}^N x_i\cdot f_i}{N}=\cfrac{7040}{150}=46,93$

Nu we het gemiddelde van de gegevens kennen, kunnen we alle benodigde kolommen toevoegen om de gemiddelde afwijking te vinden:

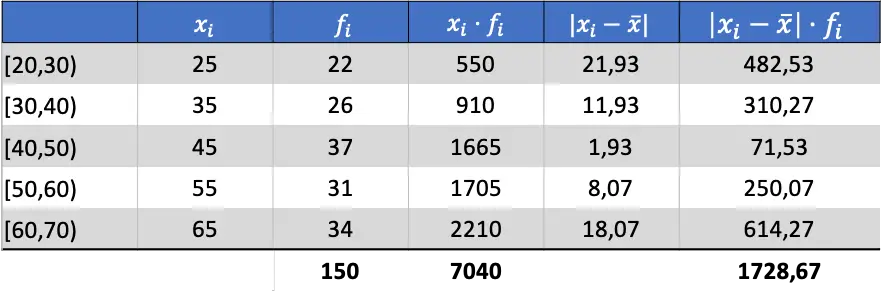
Om de gemiddelde afwijking te verkrijgen, moet u dus de som van de laatste kolom delen door het totale aantal waarnemingen:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}=\cfrac{1728,67}{150}=11,52$

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder