Hoe u de gemiddelde en standaardafwijking van gegroepeerde gegevens kunt vinden

Vaak willen we het gemiddelde en de standaarddeviatie van op de een of andere manier gegroepeerde gegevens berekenen. Stel dat we bijvoorbeeld de volgende gegroepeerde gegevens hebben:

Hoewel het niet mogelijk is om het exacte gemiddelde en de standaarddeviatie te berekenen, omdat we de ruwe gegevenswaarden niet kennen, is het wel mogelijk om het gemiddelde en de standaarddeviatie te schatten.

In de volgende stappen wordt uitgelegd hoe u dit doet.

Gerelateerd: Hoe u de gegroepeerde gegevensmodus kunt vinden

Bereken het gemiddelde van gegroepeerde gegevens

We kunnen de volgende formule gebruiken om het gemiddelde van gegroepeerde gegevens te schatten:

Gemiddeld: Σm _i n _i / N

Goud:

• _mi : Het midden van de i- ^de groep
• n _i : De frequentie van de i- ^de groep
• N: De totale steekproefomvang

Zo zouden we deze formule toepassen op onze vorige dataset:

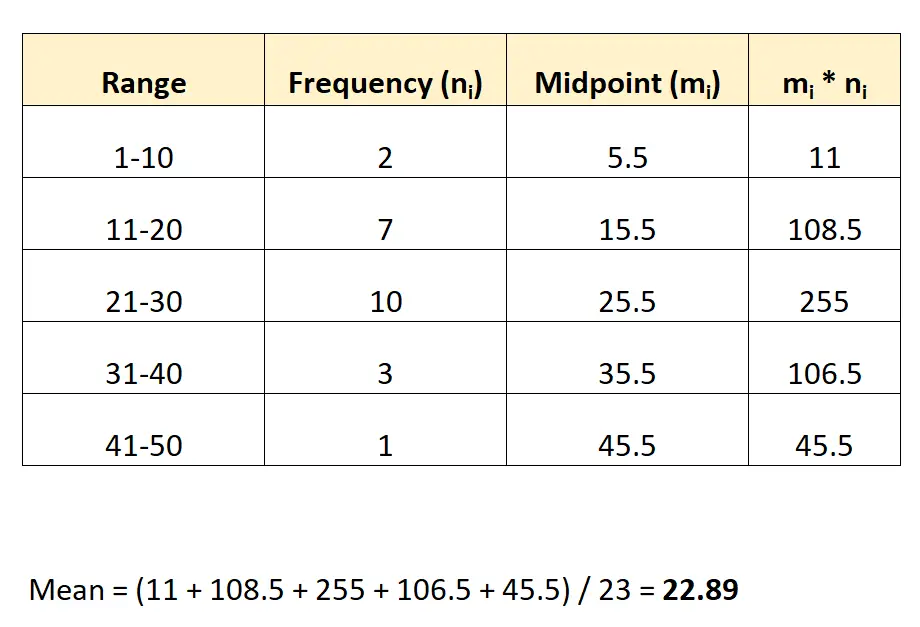
Het gemiddelde van de dataset blijkt 22,89 te zijn.

Opmerking: het middelpunt van elke groep kan worden gevonden door het gemiddelde te nemen van de onderste en bovenste waarden van het bereik. Het middelpunt van de eerste groep wordt bijvoorbeeld als volgt berekend: (1+10) / 2 = 5,5.

Bereken de standaardafwijking van gegroepeerde gegevens

We kunnen de volgende formule gebruiken om de standaardafwijking van gegroepeerde gegevens te schatten:

Standaardafwijking: √ Σn _i (m _i -μ) ² / (N-1)

Goud:

• n _i : De frequentie van de i- ^de groep
• _mi : Het midden van de i- ^de groep
• µ : Het gemiddelde
• N: De totale steekproefomvang

Zo passen we deze formule toe op onze dataset:

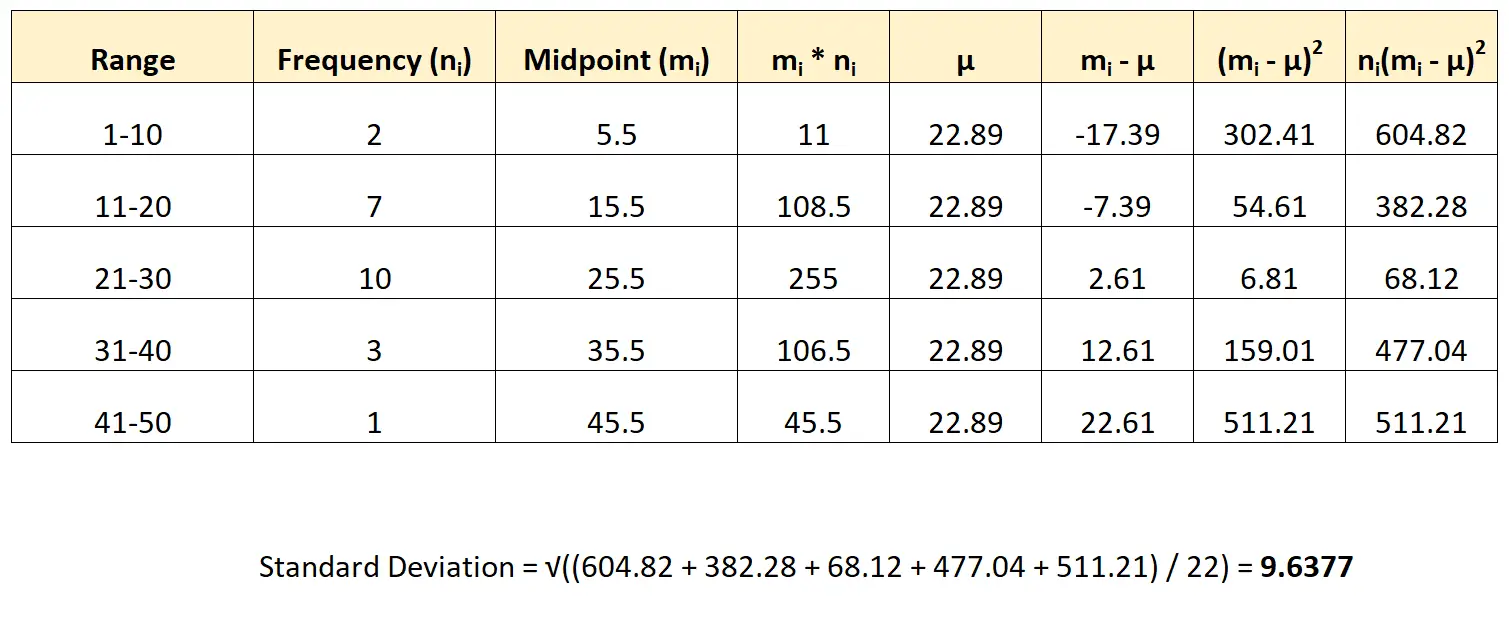De standaarddeviatie van de dataset blijkt 9,6377 te zijn.

Aanvullende bronnen

Hoe u het gemiddelde en de mediaan van elk histogram kunt schatten
Hoe u de percentielrangschikking voor gegroepeerde gegevens kunt berekenen
Hoe u de mediaan van gegroepeerde gegevens kunt vinden