Hoe u het gemiddelde van meerdere standaarddeviaties kunt vinden

Soms wilt u misschien het gemiddelde van twee of meer standaarddeviaties vinden.

Om dit te doen, kunt u, afhankelijk van uw gegevens, een van de volgende twee formules gebruiken:

Methode 1: Gelijke steekproefomvang

Als u de gemiddelde standaardafwijking tussen k- groepen wilt vinden en elke groep dezelfde steekproefomvang heeft, kunt u de volgende formule gebruiken:

Gemiddelde SD = √ (s ₁ ² + s ₂ ² + … + s _k ² ) / k

Goud:

• _sk : standaardafwijking voor de ^k- de groep
• k : Totaal aantal groepen

Methode 2: Ongelijke steekproefomvang

Als u de gemiddelde standaardafwijking tussen k- groepen wilt vinden en elke groep niet dezelfde steekproefomvang heeft, kunt u de volgende formule gebruiken:

Gemiddelde SD = √ ((n ₁ -1)s ₁ ² + (n ₂ -1)s ₂ ² + … + (n _k -1)s _k ² ) / (n ₁ +n ₂ + … + n _k – J)

Goud:

• _nk : Steekproefomvang voor de k- ^de groep
• _sk : standaardafwijking voor de ^k- de groep
• k : Totaal aantal groepen

De volgende voorbeelden laten zien hoe u elke formule in de praktijk kunt gebruiken.

Methode 1: Berekening van het gemiddelde van standaardafwijkingen voor gelijke steekproefomvang

Stel dat we de gemiddelde standaardafwijking van de verkopen over de volgende zes verkoopperioden willen berekenen:

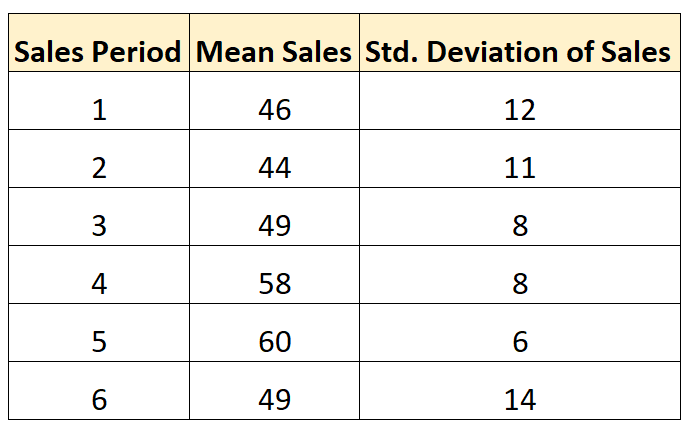
Laten we aannemen dat we tijdens elke verkoopperiode hetzelfde aantal verkooptransacties hebben uitgevoerd. Om de gemiddelde standaardafwijking van de omzet per periode te berekenen, kunnen we de volgende formule gebruiken:

• Gemiddelde standaardafwijking = √ (s ₁ ² + s ₂ ² + … + s _k ² ) / k
• Gemiddelde standaardafwijking = √ (12 ² + 11 ² + 8 ² + 8 ² + 6 ² + 14 ² ) / 6
• Gemiddelde standaardafwijking = 10,21

De gemiddelde standaardafwijking van de omzet per periode bedraagt 10,21 .

Methode 2: Het middelen van standaarddeviaties voor ongelijke steekproefomvang

Stel dat we de gemiddelde standaardafwijking van de verkopen over de volgende zes verkoopperioden willen berekenen:

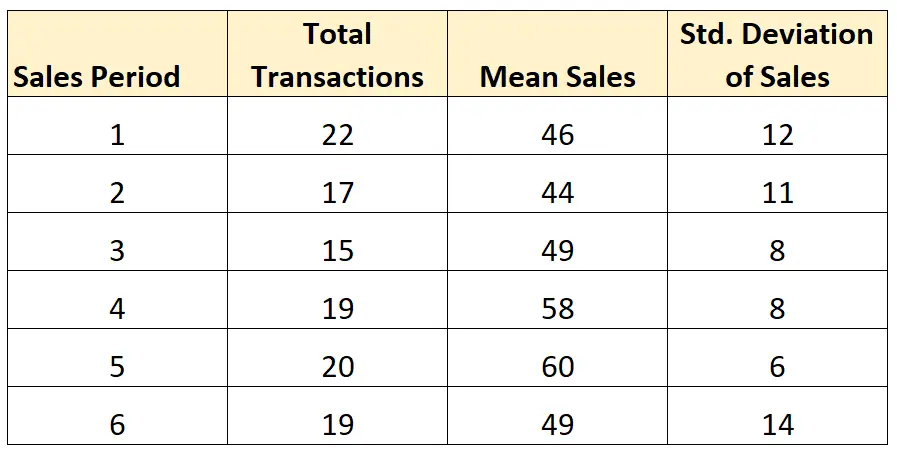
Omdat de steekproefomvang (totaal aantal transacties) niet in elke verkoopperiode gelijk is, gebruiken we de volgende formule om de gemiddelde standaardafwijking van de verkopen per periode te berekenen:

• Gemiddelde SD = √ ((n ₁ -1)s ₁ ² + (n ₂ -1)s ₂ ² + … + (n _k -1)s _k ² ) / (n ₁ +n ₂ + … + n _k – J)
• Gemiddelde SD = √ ((21)12 ² + (16)11 ² + (14)8 ² + (18)8 ² + (19)6 ² + (18)14 ² ) / 106
• Gemiddelde SD = 10,29

De gemiddelde standaardafwijking van de omzet per periode bedraagt 10,29 .

Merk op dat de gemiddelde standaarddeviatie in de twee voorbeelden vrij gelijkaardig was. Dit komt omdat de steekproefgroottes (totale transacties) in het tweede voorbeeld allemaal behoorlijk dicht bij elkaar lagen.

De twee methoden voor het berekenen van de gemiddelde standaardafwijking verschillen alleen significant als de steekproefomvang significant verschilt tussen groepen.