De relatie tussen gemiddelde en standaarddeviatie (met voorbeeld)

Het gemiddelde vertegenwoordigt de gemiddelde waarde in een reeks gegevens.

Het wordt als volgt berekend:

Steekproefgemiddelde = Σx _i / n

Goud:

• Σ: Een symbool dat “som” betekent
• x _i : De i- ^de waarneming in een dataset
• n: het totale aantal waarnemingen in de dataset

De standaardafwijking vertegenwoordigt de verdeling van waarden in een dataset ten opzichte van het gemiddelde.

Het wordt als volgt berekend:

Standaardafwijking van de steekproef = √ Σ(x _i – x _bar ) ² / (n-1)

Goud:

• Σ: Een symbool dat “som” betekent
• x _i : de ^i- de waarde van het monster
• x _bar : Het steekproefgemiddelde
• n: De steekproefomvang

Let op de relatie tussen het gemiddelde en de standaardafwijking: het gemiddelde wordt in de formule gebruikt om de standaardafwijking te berekenen .

In feite kunnen we de standaarddeviatie van een steekproef niet berekenen tenzij we het steekproefgemiddelde kennen.

Het volgende voorbeeld laat zien hoe u het steekproefgemiddelde en de steekproefstandaarddeviatie voor een gegevensset in de praktijk kunt berekenen.

Voorbeeld: Berekening van de gemiddelde en standaarddeviatie voor een dataset

Laten we zeggen dat we de volgende dataset hebben die de punten toont die door 10 verschillende basketbalspelers zijn gescoord:

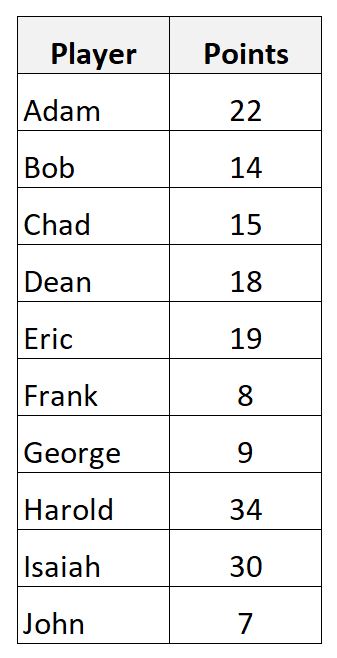We kunnen het steekproefgemiddelde van de gescoorde punten berekenen met behulp van de volgende formule:

• Steekproefgemiddelde = Σx _i / n
• Steekproefgemiddelde = (22+14+15+18+19+8+9+34+30+7) / 10
• Steekproefgemiddelde = 17,6

Het steekproefgemiddelde van de gescoorde punten bedraagt 17,6 . Dit vertegenwoordigt het gemiddelde aantal gescoorde punten van alle spelers.

Zodra we het steekproefgemiddelde kennen, kunnen we dit in de formule invoeren om de standaarddeviatie van de steekproef te berekenen:

• Standaardafwijking van de steekproef = √ Σ(x _i – x _bar ) ² / (n-1)
• Standaardafwijking van de steekproef = √ ((22-17,6) ² + (14-17,6) ² + (15-17,6) ² + (18-17,6) ² + (19-17,6) 6) ² + (8-17,6) ² + (9 -17,6) ² + (34-17,6) ² + (30-17,6) ² + (7-17,6) ² ) / (10-1)
• Standaarddeviatie van de steekproef = 9,08

De standaarddeviatie van de steekproef is 9,08 . Dit vertegenwoordigt de gemiddelde afstand tussen elke puntwaarde en het monsterpuntgemiddelde.

Het is handig om zowel het gemiddelde als de standaardafwijking van een dataset te kennen, omdat elke metriek ons iets anders vertelt.

Het gemiddelde geeft ons een idee waar de ‘centrale’ waarde van een dataset ligt.

De standaarddeviatie geeft ons een idee van de verdeling van waarden rond het gemiddelde in een dataset. Hoe hoger de standaarddeviatiewaarde, hoe meer verspreid de waarden in een steekproef zijn.

Door deze twee waarden te kennen, kunnen we veel leren over de verdeling van waarden in een dataset.

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over het gemiddelde en de standaarddeviatie:

Waarom is het gemiddelde belangrijk in statistieken?
Waarom is standaarddeviatie belangrijk in statistieken?
Hoe gemiddelde en standaarddeviatie in Excel te berekenen