Geometrische middelen

Von Dr.benjamin anderson August 6, 2023 Statistieken Keine Kommentare

In dit artikel leggen we uit wat meetkundig gemiddelde is, hoe het wordt berekend en wat het verschil is tussen meetkundig gemiddelde en rekenkundig gemiddelde. U zult ook een stap voor stap opgeloste oefening van het geometrische gemiddelde kunnen zien en wat de eigenschappen van dit type gemiddelde zijn. Ten slotte vindt u een rekenmachine waarmee u het geometrische gemiddelde van elke dataset kunt berekenen.

Wat is het geometrische gemiddelde?

Het geometrische gemiddelde is een maatstaf voor de centrale plaats van beschrijvende statistieken. Het geometrische gemiddelde van een reeks statistische gegevens is gelijk aan de n-de wortel van het product van alle waarden.

Het geometrische gemiddelde wordt in de bedrijfsfinanciering gebruikt om rendementen, procentuele gemiddelden en samengestelde rente te berekenen.

De formule voor het geometrische gemiddelde is daarom als volgt:

Het geometrische gemiddelde kan alleen worden berekend als alle gegevens in de steekproef positief zijn. Omdat als een waarde negatief is, de wortel een negatieve oplossing of geen oplossing zou hebben. Als een gegeven daarentegen nul is, zou de vermenigvuldiging van de gegevens nul opleveren en daarom zou het geometrische gemiddelde gelijk zijn aan 0.

Het geometrische gemiddelde is niet het enige type gemiddelde dat bestaat; er zijn ook het rekenkundige gemiddelde, het gewogen gemiddelde, het kwadratische gemiddelde en het harmonische gemiddelde.

Verschil tussen meetkundig gemiddelde en rekenkundig gemiddelde

Het belangrijkste verschil tussen het geometrische gemiddelde en het rekenkundige gemiddelde is dat het geometrische gemiddelde minder gevoelig is voor extreme waarden dan het rekenkundig gemiddelde. Bovendien kan het rekenkundig gemiddelde worden berekend met negatieve en nulwaarden, terwijl het geometrische gemiddelde alleen met positieve waarden kan worden berekend.

Op dezelfde manier zal het geometrische gemiddelde over het algemeen lager zijn dan het rekenkundige gemiddelde voor dezelfde gegevensset.

Er moet ook worden opgemerkt dat de berekening van het geometrische gemiddelde complexer is en dat de statistische significantie ervan daarom moeilijker te interpreteren is.

Kortom, het geometrische gemiddelde heeft voor- en nadelen vergeleken met het rekenkundig gemiddelde en afhankelijk van de aard van de gegevens zal het passend zijn om dit of dat gemiddelde te berekenen.

Hoe het geometrische gemiddelde te berekenen

Om het geometrische gemiddelde te berekenen, moeten de volgende stappen worden uitgevoerd:

Bereken het product van alle statistische gegevens in de steekproef.
Zoek de n-de wortel van het berekende product.
Het verkregen resultaat is het geometrische gemiddelde van de statistische steekproef.

Zoals u kunt zien, is het vinden van het geometrische gemiddelde van een reeks gegevens relatief eenvoudig met een rekenmachine of een computerprogramma, omdat u alleen een product en een wortel hoeft te berekenen. Integendeel, het is behoorlijk omslachtig om de berekening met de hand uit te voeren.

👉 Daarom raden we aan de onderstaande rekenmachine te gebruiken om het geometrische gemiddelde van een dataset te berekenen.

Geometrisch gemiddelde voorbeeld

Zodra we de theorie over het geometrische gemiddelde hebben gezien, zullen we een voorbeeld maken, zodat je precies kunt zien hoe je het geometrische gemiddelde kunt verkrijgen.

De economische resultaten van een bedrijf over de afgelopen vijf jaar zijn bekend. In het eerste jaar genereerde het bedrijf een economische winstgevendheid van 10%, in het tweede jaar bereikte de winst 23%, in het derde jaar bedroeg het verdiende geld 16%, in het vierde jaar behaalde het een economische winstgevendheid van 7% en de investeringen in het vijfde jaar vertegenwoordigde een rendement van 20%. U wordt gevraagd het gemiddelde van alle percentages te berekenen.

Zoals we hebben gezien, moet je om het gemiddelde van de percentages te berekenen niet het rekenkundig gemiddelde gebruiken, maar de berekening uitvoeren met het geometrische gemiddelde.

Daarom passen we de formule voor het geometrische gemiddelde toe:

$MG=\sqrt[n]{\prod_{i=1}^Nx_i}=\sqrt[n]{x_1\cdot x_2\cdot \ldots x_n}$

En we vervangen de voorbeeldwaarden in de formule en voeren de berekening uit:

$MG=\sqrt[5]{1,10\cdot 1,23\cdot 1,16\cdot 1,07\cdot 1,20}=1,15 \ \longrightarrow \ 15 \%$

Merk op dat we vijf gegevenspunten hebben, dus we berekenen de vijfde wortel.

De numerieke uitkomst van het geometrische gemiddelde is 1,15, wat betekent dat het bedrijf jaarlijks een economische groei van gemiddeld 15% kende.

Houd er rekening mee dat we het geometrische gemiddelde konden achterhalen omdat alle waarden positief waren, maar als een percentage negatief was geweest, hadden we de gegevens in de formule moeten plaatsen als een positieve decimaal met het gehele deel. gelijk aan nul. Een groei van -30% moet in de formule bijvoorbeeld worden uitgedrukt als 0,70 (1-0,3=0,7).

Geometrische gemiddelde rekenmachine

Sluit een voorbeeldstatistiek aan op de onderstaande rekenmachine om het geometrische gemiddelde ervan te vinden. Gegevens moeten worden gescheiden door een spatie en moeten worden ingevoerd met de punt als decimaal scheidingsteken. Houd er rekening mee dat u het geometrische gemiddelde niet kunt bepalen als een waarde negatief of nul is.

Eigenschappen van het geometrische gemiddelde

Het geometrische gemiddelde heeft de volgende kenmerken:

Dit is een type gemiddelde dat erg handig is om het gemiddelde van percentages of indices te vinden.

Het kan alleen worden berekend als alle gegevens positief zijn.

De geometrische betekenis van het geometrische gemiddelde van twee getallen a en b is de zijde van een vierkant met dezelfde oppervlakte als de rechthoek waarvan de zijden a en b zijn.

$MG(a,b)=\sqrt{a\cdot b}$

De geometrische betekenis van het geometrische gemiddelde van drie getallen a , b en c is de zijde van een kubus waarvan het volume gelijk is aan het parallellepipedum van zijden a , b en c .

$MG(a,b,c)=\sqrt[3]{a\cdot b \cdot c}$

De logaritme van het geometrische gemiddelde van een reeks gegevens geeft het rekenkundige gemiddelde van de logaritmen van dezelfde reeks.

Het geometrische gemiddelde van een reeks waarden zal altijd kleiner zijn dan of gelijk zijn aan het rekenkundig gemiddelde.

$\sqrt[N]{x_1\cdot x_2\ldots x_N}\leq \cfrac{x_1+x_2+\ldots+x_N}{N}$

Het gewogen geometrische gemiddelde wordt op dezelfde manier berekend als het geometrische gemiddelde, maar door gewichten toe te voegen aan de exponent van elk gegevensitem om de statistische waarden te wegen.

$\displaystyle \left(\prod_{i=1}^n{x_i}^{\alpha_i}\right)^{\frac{1}{\sum_i{\alpha_i}}}= \left({x_1}^{\alpha_1}{x_2}^{\alpha_2}\dots{x_n}^{\alpha_n}\right)^{ \frac{1}{\alpha_1+ \dots+ \alpha_n}} \left}}$

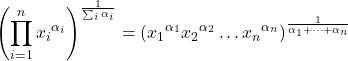
Bereken het geometrische gemiddelde in Excel

Laten we tot slot kijken hoe we het geometrische gemiddelde van een gegevensset kunnen vinden met behulp van het Excel-programma.

Om het geometrische gemiddelde in Excel te berekenen, moet u de functie MEANS.GEOM gebruiken. Voer eenvoudigweg alle waarden in waarvan u het geometrische gemiddelde wilt nemen en de functie retourneert het resultaat van het geometrische gemiddelde.

Om bijvoorbeeld het geometrische gemiddelde van het bovenstaande voorbeeld te bepalen, moet u in een Excel-vak =MEDIA.GEOM(1.1;1.23;1.16;1.07;1.20) schrijven.

Houd er rekening mee dat als een van de waarden nul of negatief is, de functie een fout retourneert.

Zoals u kunt zien, is het veel eenvoudiger en sneller om met Excel een geometrisch gemiddelde te berekenen, omdat u de gegevens alleen maar naar een blad hoeft te kopiëren en een formule hoeft te gebruiken.

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder