Een inleiding tot geometrische distributie

De geometrische verdeling beschrijft de kans op het ervaren van een bepaald aantal mislukkingen voordat het eerste succes in een reeks Bernoulli-proeven wordt ervaren.

Een Bernoulli-proef is een experiment met slechts twee mogelijke uitkomsten – ‘succes’ of ‘mislukking’ – en de kans op succes is elke keer dat het experiment wordt uitgevoerd hetzelfde.

Een voorbeeld van een Bernoulli-essay is het opgooien van munten. De munt kan slechts op twee kop landen (we zouden kop een „hit“ kunnen noemen en staart een „mislukking“) en de kans op succes bij elke opgooi is 0,5, ervan uitgaande dat de munt eerlijk is.

Als een willekeurige variabele X een geometrische verdeling volgt, kan de kans op k mislukkingen voordat het eerste succes wordt ervaren, worden gevonden met de volgende formule:

P(X=k) = (1-p) ^kp

Goud:

• k: aantal mislukkingen vóór het eerste succes
• p: kans op succes bij elke proef

Laten we bijvoorbeeld zeggen dat we willen weten hoe vaak we een eerlijke munt moeten opgooien voordat deze kop oplevert. We kunnen de bovenstaande formule gebruiken om de waarschijnlijkheid van 0, 1, 2, 3 storingen, enz. te bepalen. voordat de munt op kop landt:

Let op: de munt kan 0 “mislukking” ervaren als hij bij de eerste worp kop oplevert.

P(X=0) = (1-.5) ⁰ (.5) = 0,5

P(X=1) = (1-.5) ¹ (.5) = 0,25

P(X=2) = (1-.5) ² (.5) = 0,125

P(X=3) = (1-0,5) ³ (0,5) = 0,0625

We kunnen de waarschijnlijkheid van een willekeurig aantal muntopgooien tot in het oneindige berekenen. Vervolgens maken we een eenvoudig histogram om deze waarschijnlijkheidsverdeling te visualiseren:

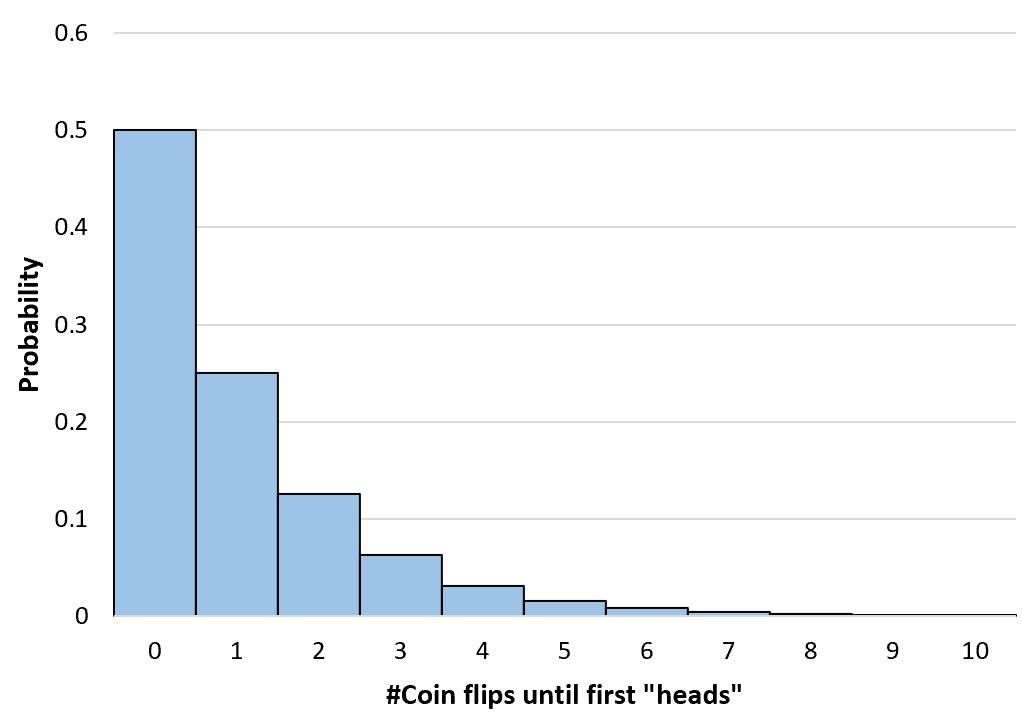
Berekening van cumulatieve geometrische kansen

De cumulatieve waarschijnlijkheid dat we k of minder mislukkingen ervaren tot het eerste succes kan worden gevonden met de volgende formule:

P(X≤k) = 1 – (1-p) ^k+1

Goud:

• k: aantal mislukkingen vóór het eerste succes
• p: kans op succes bij elke proef

Stel dat we bijvoorbeeld willen weten hoe waarschijnlijk het is dat er drie of minder “missers” nodig zijn voordat de munt uiteindelijk op kop terechtkomt. Om deze waarschijnlijkheid te berekenen, gebruiken we de volgende formule:

P(X≤3) = 1 – (1-0,5) ³⁺¹ = 0,9375

We kunnen elke cumulatieve waarschijnlijkheid berekenen met behulp van een vergelijkbare formule:

P(X≤0) = 1 – (1-.5) ⁰⁺¹ = 0,5

P(X≤1) = 1 – (1-0,5) ¹⁺¹ = 0,75

P(X≤2) = 1 – (1-0,5) ²⁺¹ = 0,875

We kunnen deze cumulatieve kansen berekenen voor een willekeurig aantal muntopgooien tot in het oneindige. We kunnen vervolgens een histogram maken om deze cumulatieve waarschijnlijkheidsverdeling te visualiseren:

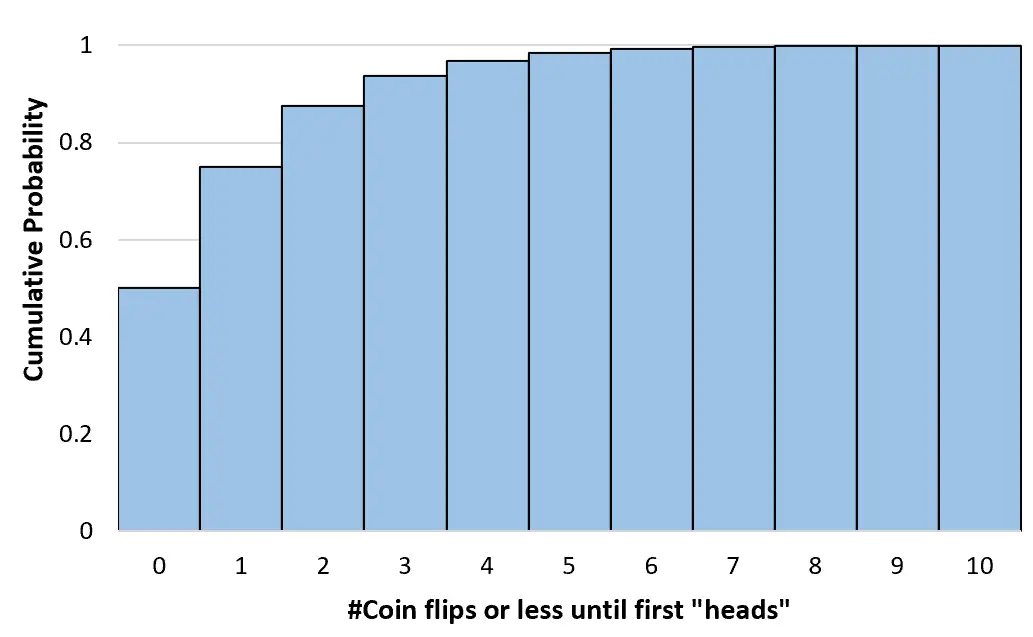
Eigenschappen van geometrische distributie

De geometrische verdeling heeft de volgende eigenschappen:

Het gemiddelde van de verdeling is (1-p) / p .

De variantie van de verdeling is (1-p) / p ² .

Bijvoorbeeld:

Het gemiddelde aantal keren dat we verwachten dat een munt kop landt voordat munt landt, is (1-p) / p = (1-.5) / .5 = 1 .

De variantie van het aantal worpen totdat het op kop terechtkomt, zou (1-p)/ ^p2 =(1-.5)/ zijn. ⁵² = 2 .

Oefenproblemen met geometrische distributie

Gebruik de volgende oefenproblemen om uw kennis van geometrische distributie te testen.

Opmerking: we zullen de Geometrische Verdelingscalculator gebruiken om de antwoorden op deze vragen te berekenen.

Probleem 1

Vraag: Een onderzoeker wacht buiten een bibliotheek om mensen te vragen of zij een bepaalde wet steunen. De kans dat een bepaalde persoon de wet steunt is p = 0,2. Hoe groot is de kans dat de vierde persoon met wie de onderzoeker spreekt de eerste zal zijn die de wet steunt?

Antwoord: Het aantal “mislukkingen” tot het eerste succes – dat wil zeggen het aantal mensen dat de wet niet steunt totdat de eerste persoon deze steunt – is 3. Dus bij gebruik van de geometrische verdelingscalculator met p = 0,2 en x = 3 mislukkingen, we vinden dat P(X=3) = 0,10240 .

Probleem 2

Vraag: Een onderzoeker wacht buiten een bibliotheek om mensen te vragen of zij een bepaalde wet steunen. De kans dat een bepaalde persoon de wet steunt is p = 0,2. Hoe groot is de kans dat de onderzoeker met meer dan vier mensen moet praten om iemand te vinden die de wet steunt?

Antwoord: Met behulp van de geometrische verdelingscalculator met p =0,2 en x = 4 fouten, vinden we dat P(X>4) = 0,32768 .

Probleem 3

Vraag: Een onderzoeker wacht buiten een bibliotheek om mensen te vragen of zij een bepaalde wet steunen. De kans dat een bepaalde persoon de wet steunt is p = 0,2. Met hoeveel mensen zal de onderzoeker naar verwachting moeten praten totdat ze iemand vindt die de wet steunt?

Antwoord: Bedenk dat het gemiddelde van de geometrische verdeling (1-p) / p is. In deze situatie zou het gemiddelde (1-.2) / .2 = 4 zijn.