Gepaarde monsters t-test: definitie, formule en voorbeeld

Een paired samples t-test wordt gebruikt om de gemiddelden van twee monsters te vergelijken wanneer elke waarneming in het ene monster kan worden geassocieerd met een waarneming in het andere monster.

In deze zelfstudie wordt het volgende uitgelegd:

• De motivatie om een paired samples t-test uit te voeren.
• De formule voor het uitvoeren van een t-test met gepaarde monsters.
• De aannames waaraan moet worden voldaan om een t-test met gepaarde monsters uit te voeren.
• Een voorbeeld van hoe u een t-test met gepaarde monsters uitvoert.

Gepaarde monsters t-test: motivatie

Een paired samples t-test wordt vaak gebruikt in twee scenario’s:

1. Voor en na een behandeling wordt bij een onderwerp een meting gedaan . Zo wordt bijvoorbeeld de maximale verticale sprong van universiteitsbasketbalspelers gemeten voor en na deelname aan een trainingsprogramma.

2. Er wordt onder twee verschillende omstandigheden een meting uitgevoerd – de responstijd van een patiënt wordt bijvoorbeeld gemeten met twee verschillende medicijnen.

In beide gevallen willen we de gemiddelde meting tussen twee groepen vergelijken, waarbij elke waarneming uit het ene monster geassocieerd kan worden met een waarneming uit het andere monster.

Gepaarde monsters t-test: formule

Een paired samples t-test gebruikt altijd de volgende nulhypothese:

• H ₀ : μ ₁ = μ ₂ (de twee populatiegemiddelden zijn gelijk)

De alternatieve hypothese kan bilateraal, links of rechts zijn:

• H ₁ (tweezijdig): μ ₁ ≠ μ ₂ (de gemiddelden van de twee populaties zijn niet gelijk)
• H ₁ (links): μ ₁ < μ ₂ (het gemiddelde van populatie 1 is lager dan het gemiddelde van populatie 2)
• H ₁ (rechts): μ ₁ > μ ₂ (het gemiddelde van populatie 1 is groter dan het gemiddelde van populatie 2)

We gebruiken de volgende formule om de t-teststatistiek te berekenen:

t = x _diff / (s _diff /√n)

Goud:

• x _diff : voorbeeld van het gemiddelde van de verschillen
• s: voorbeeld van standaardafwijking van verschillen
• n: steekproefgrootte (dwz aantal paren)

Als de p-waarde die overeenkomt met de t-toetsstatistiek met (n-1) vrijheidsgraden kleiner is dan het gekozen significantieniveau (veel voorkomende keuzes zijn 0,10, 0,05 en 0,01), dan kun je de nulhypothese verwerpen.

Gepaarde monsters t-test: aannames

Om de resultaten van een paired samples t-test geldig te laten zijn, moet aan de volgende aannames worden voldaan:

• Deelnemers moeten willekeurig uit de populatie worden geselecteerd.
• De verschillen tussen paren moeten ongeveer normaal verdeeld zijn.
• Er mogen geen extreme uitschieters in de verschillen voorkomen.

Gepaarde monsters t-test : voorbeeld

Stel dat we willen weten of een bepaald trainingsprogramma al dan niet in staat is om de maximale verticale sprong (in inches) van universiteitsbasketbalspelers te vergroten.

Om dit te testen, kunnen we een eenvoudige willekeurige steekproef van twintig universiteitsbasketbalspelers rekruteren en elk van hun maximale verticale sprongen meten. Dan kunnen we elke speler een maand lang het trainingsprogramma laten gebruiken en aan het einde van de maand opnieuw zijn maximale verticale sprong meten.

Om te bepalen of het trainingsprogramma daadwerkelijk een effect heeft gehad op de maximale verticale sprong, zullen we een paired samples t-test uitvoeren op het significantieniveau α = 0,05 met behulp van de volgende stappen:

Stap 1: Bereken samenvattende gegevens voor de verschillen.

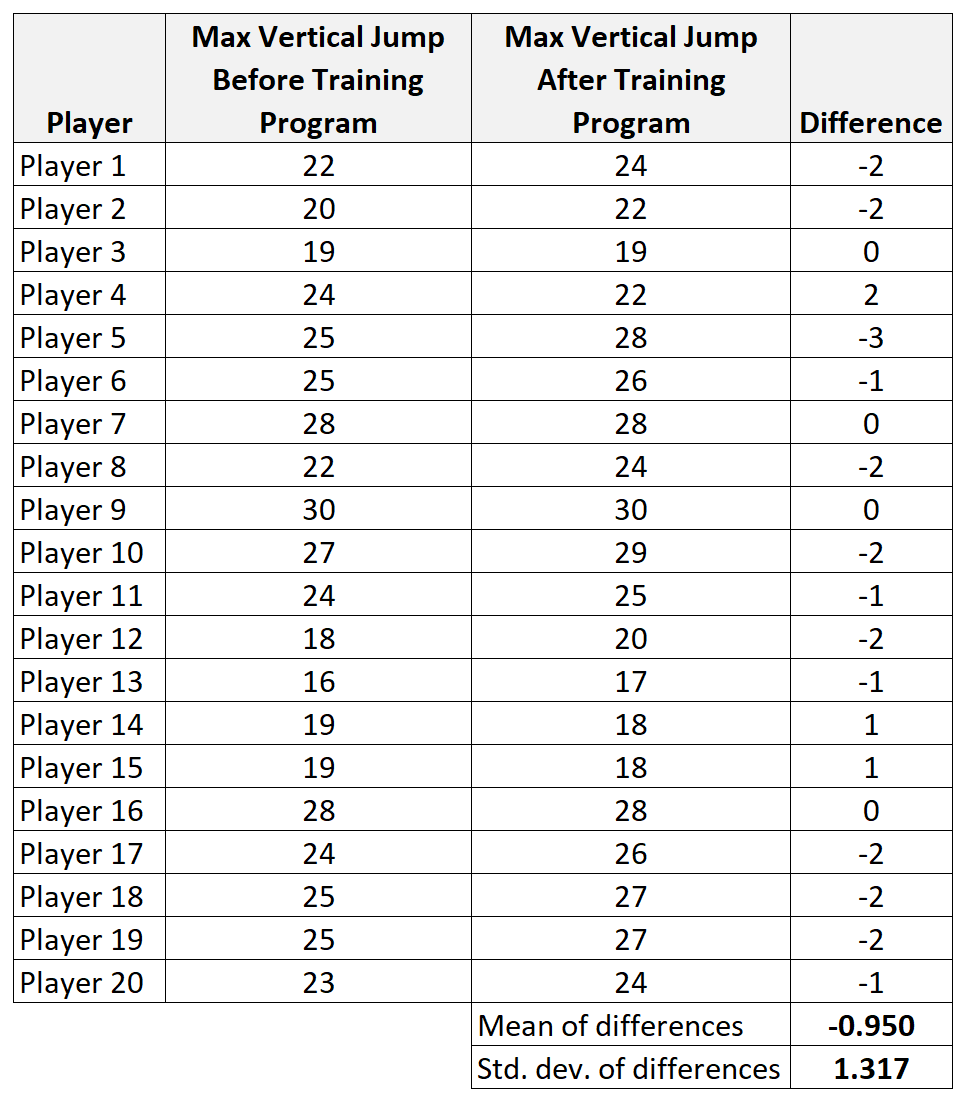
• x _diff : steekproefgemiddelde van verschillen = -0,95
• s: steekproefstandaardafwijking van verschillen = 1,317
• n: steekproefgrootte (dwz aantal paren) = 20

Stap 2: Definieer aannames.

We zullen de t-test uitvoeren voor gepaarde steekproeven met de volgende hypothesen:

• H ₀ : μ ₁ = μ ₂ (de twee populatiegemiddelden zijn gelijk)
• H ₁ : μ ₁ ≠ μ ₂ (de twee populatiegemiddelden zijn niet gelijk)

Stap 3: Bereken de t -teststatistiek.

t = x _verschil / (s _verschil /√n) = -0,95 / (1,317/ √ 20) = -3,226

Stap 4: Bereken de p-waarde van de t- teststatistiek.

Volgens de T-score naar P-waardecalculator is de p-waarde geassocieerd met t = -3,226 en vrijheidsgraden = n-1 = 20-1 = 19 0,00445 .

Stap 5: Trek een conclusie.

Omdat deze p-waarde onder ons significantieniveau α = 0,05 ligt, verwerpen we de nulhypothese. We hebben voldoende bewijs om te zeggen dat de gemiddelde maximale verticale sprong van spelers verschillend is voor en na deelname aan het trainingsprogramma.

Opmerking: u kunt deze volledige paired-samples t-test ook uitvoeren door eenvoudigweg de paired-samples t-test-calculator te gebruiken.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u een t-test met gepaarde steekproeven kunt uitvoeren met behulp van verschillende statistische programma’s:

Een t-test met gepaarde monsters uitvoeren in Excel
Hoe u een paired samples t-test uitvoert in SPSS
Hoe u een paired samples t-test uitvoert in Stata
Een t-test met gepaarde steekproeven uitvoeren op een TI-84-rekenmachine
Hoe voer je een paired samples t-test uit in R
Hoe u een gepaarde samples t-test uitvoert in Python
Een T-test met gepaarde monsters met de hand uitvoeren