Een t-test met gepaarde monsters uitvoeren in excel

Een paired samples t-test wordt gebruikt om de gemiddelden van twee monsters te vergelijken wanneer elke waarneming in het ene monster kan worden geassocieerd met een waarneming in het andere monster.

In deze zelfstudie wordt uitgelegd hoe u een t-test met gepaarde monsters uitvoert in Excel.

Een t-test met gepaarde monsters uitvoeren in Excel

Stel dat we willen weten of een bepaald curriculum een significante impact heeft op de prestaties van studenten op een bepaald examen. Om dit te testen, vragen we 20 leerlingen in een klas een voortoets te maken. Vervolgens laten we alle leerlingen twee weken lang deelnemen aan het lesprogramma. Vervolgens maken de leerlingen opnieuw een toets met dezelfde moeilijkheidsgraad.

Om het verschil tussen de gemiddelde scores op de eerste en tweede toets te vergelijken, gebruiken we een paired samples t-toets, omdat voor elke leerling zijn score op de eerste toets kan worden geassocieerd met zijn score op de tweede toets.

De volgende afbeelding toont de pre-testscore en de post-testscore van elke leerling:

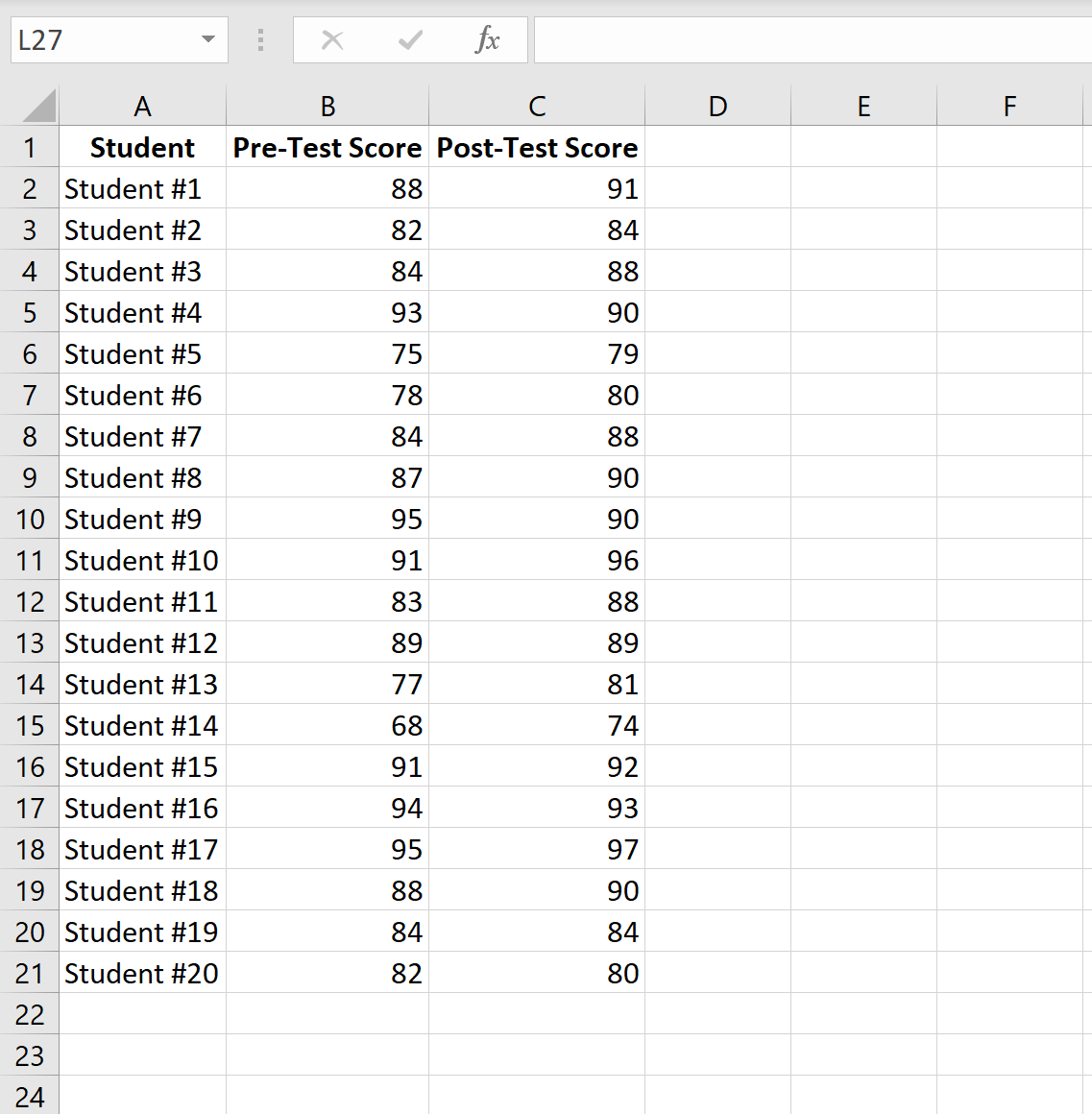
Voer de volgende stappen uit om een t-test met gepaarde monsters uit te voeren om te bepalen of er een significant verschil is in de gemiddelde testscores tussen de pre-test en de post-test.

Stap 1: Open het Data Analysis ToolPak.

Klik op het tabblad Gegevens van het bovenste lint op ‚Gegevensanalyse‘.

Als u deze optie om te klikken niet ziet, moet u eerst het Analysis ToolPak downloaden , dat volledig gratis is.

Stap 2: Selecteer de juiste test die u wilt gebruiken.

Selecteer de optie met de tekst T-Test: Paired Two Sample for Means en klik vervolgens op OK.

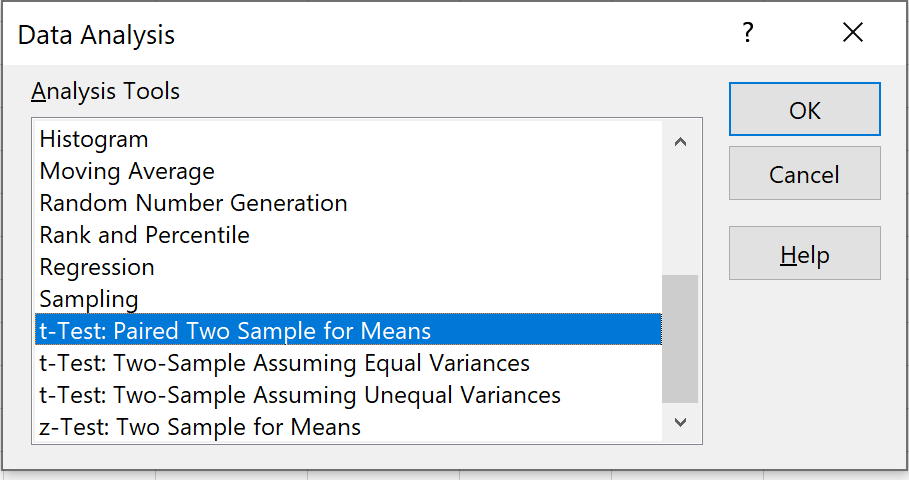
Stap 3: Voer de benodigde informatie in.

Voer het bereik van waarden in voor variabele 1 (de pre-testscores), variabele 2 (de post-testscores), het hypothetische gemiddelde verschil (in dit geval plaatsen we „0“ omdat we willen weten of het werkelijke verschil het gemiddelde tussen de pre-test- en post-testscores is 0), en het uitvoerbereik waarin we de testresultaten graag weergegeven willen zien. Klik vervolgens op OK.

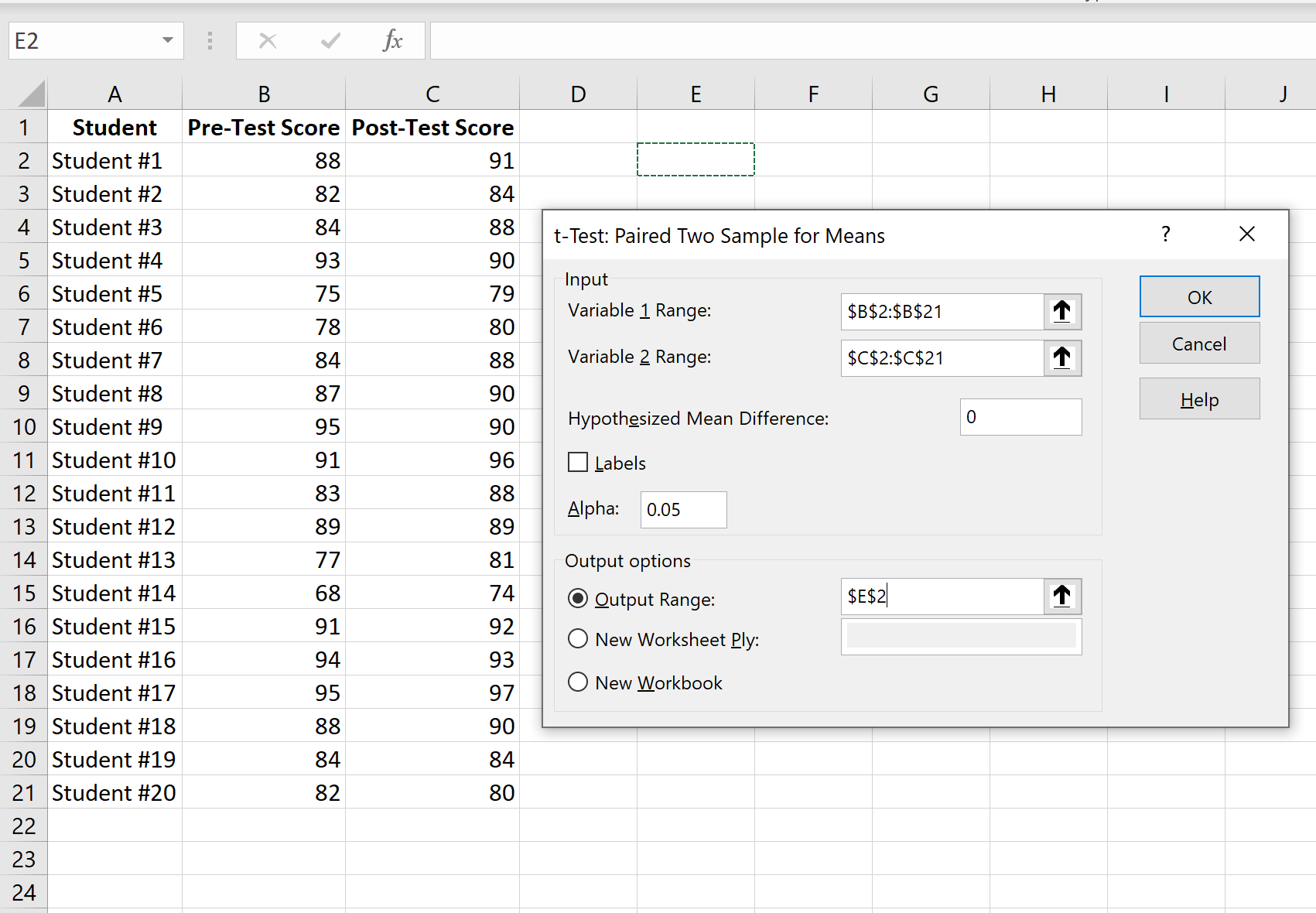
Stap 4: Interpreteer de resultaten.

Zodra u in de vorige stap op OK klikt, worden de t-testresultaten weergegeven.

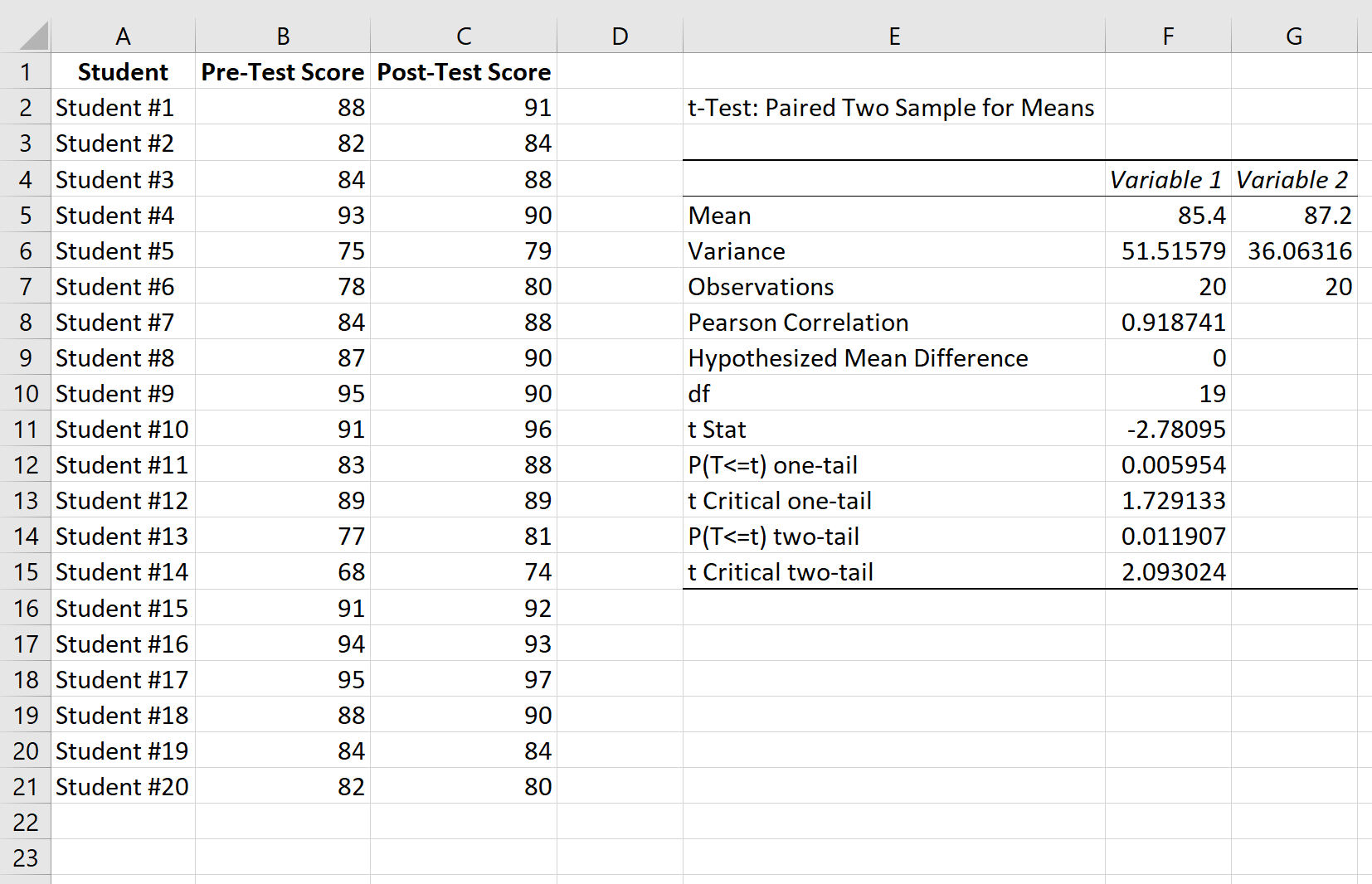
Zo interpreteert u de resultaten:

Gemiddelde: Dit is het gemiddelde van elk monster. De gemiddelde pre-testscore is 85,4 en de gemiddelde post-testscore is 87,2 .

Variantie: Dit is de variantie voor elk monster. De variantie van de pre-testscores is 51,51 en de variantie van de post-testscores is 36,06 .

Waarnemingen: Dit is het aantal waarnemingen in elk monster. Beide monsters bevatten 20 waarnemingen.

Pearson-correlatie: de correlatie tussen scores vóór de test en scores na de test. Het blijkt 0,918 te zijn.

Hypothetisch gemiddeld verschil: Het getal waarover we ‘hypotheteren’ is het verschil tussen de twee gemiddelden. In dit geval hebben we 0 gekozen omdat we willen testen of er al dan niet een verschil is tussen de pre-test- en post-testscores.

df: de vrijheidsgraden voor de t-toets. Dit wordt berekend als n-1 waarbij n het aantal paren is. In dit geval is df = 20 – 1 = 19 .

t Stat: De t- teststatistiek, die -2,78 blijkt te zijn.

Tweezijdige P(T<=t): de p-waarde voor een tweezijdige t-toets. In dit geval is p = 0,011907 . Dit is kleiner dan alfa = 0,05, dus we verwerpen de nulhypothese. We hebben voldoende bewijs om te zeggen dat er een statistisch significant verschil bestaat tussen de gemiddelde score vóór en na de test.

t Tweezijdig kritisch: Dit is de kritische waarde van de test, gevonden door de waarde in de t-verdelingstabel te identificeren die overeenkomt met een tweezijdige test met alpha = 0,05 en df = 19. Dit blijkt 2 te zijn, 093024 . Omdat de absolute waarde van onze t -teststatistiek groter is dan deze waarde, verwerpen we de nulhypothese. We hebben voldoende bewijs om te zeggen dat er een statistisch significant verschil bestaat tussen de gemiddelde score vóór en na de test.

Merk op dat de p-waarde en de kritische-waardebenadering beide tot dezelfde conclusie zullen leiden.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere t-tests in Excel uitvoert:

Hoe u een t-test met één monster uitvoert in Excel
Hoe u een t-test met twee steekproeven uitvoert in Excel