De drie hypothesen geformuleerd in een gepaarde t-toets

Een paired samples t-test wordt gebruikt om de gemiddelden van twee monsters te vergelijken wanneer elke waarneming in het ene monster kan worden geassocieerd met een waarneming in het andere monster.

Bij dit type test worden de volgende aannames gedaan over de gegevens:

1. Onafhankelijkheid: elke waarneming moet onafhankelijk zijn van elke andere waarneming.

2. Normaliteit: De verschillen tussen paren moeten ongeveer normaal verdeeld zijn.

3. Geen extreme uitschieters: Er mogen geen extreme uitschieters in de verschillen voorkomen.

Als niet aan een of meer van deze aannames wordt voldaan, kunnen de resultaten van de t-test voor gepaarde monsters onbetrouwbaar of misleidend zijn.

In deze zelfstudie geven we uitleg over elke aanname, hoe u kunt bepalen of aan de aanname is voldaan en wat u moet doen als deze wordt geschonden.

Hypothese 1: Onafhankelijkheid

Een paired samples t-test gaat ervan uit dat elke waarneming onafhankelijk is van alle andere waarnemingen.

Hoe deze hypothese te verifiëren

De eenvoudigste manier om deze aanname te verifiëren is door te verifiëren dat elke waarneming is verzameld met behulp van een willekeurige steekproefmethode .

Als er een willekeurige steekproefmethode is gebruikt (zoals eenvoudige willekeurige steekproeven), kunnen we aannemen dat elke waarneming onafhankelijk is van alle andere waarnemingen.

Wat te doen als deze veronderstelling niet wordt gerespecteerd

Als niet aan deze aanname wordt voldaan, zijn de resultaten van de t-test met gepaarde monsters volledig ongeldig.

In dit scenario is het het beste om nieuwe waarnemingen te verzamelen met behulp van een willekeurige steekproefmethode om ervoor te zorgen dat elke waarneming onafhankelijk is.

Hypothese 2: normaliteit

Bij een paired samples t-test wordt ervan uitgegaan dat de verschillen tussen paren bij benadering normaal verdeeld moeten zijn.

Dit is een cruciale aanname, want als de verschillen tussen paren niet normaal verdeeld zijn, is het niet geldig om de p-waarde van de test te gebruiken om conclusies te trekken.

Hoe deze hypothese te verifiëren

De eenvoudigste manier om deze hypothese te testen is door eenvoudigweg een histogram van de gepaarde verschillen te maken en visueel te controleren of het histogram al dan niet een belvorm heeft.

Als het histogram er bijvoorbeeld zo uitziet, zouden we zeggen dat aan de normaliteitsaanname is voldaan:

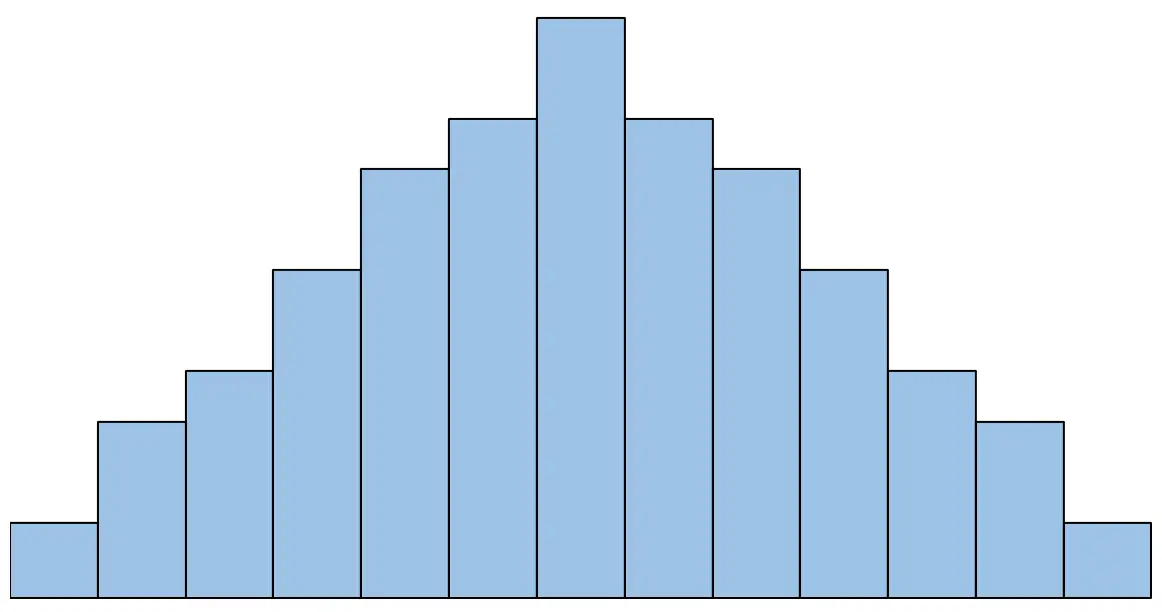
Als het histogram er echter zo uitziet, zouden we zeggen dat niet aan de normaliteitsaanname is voldaan:

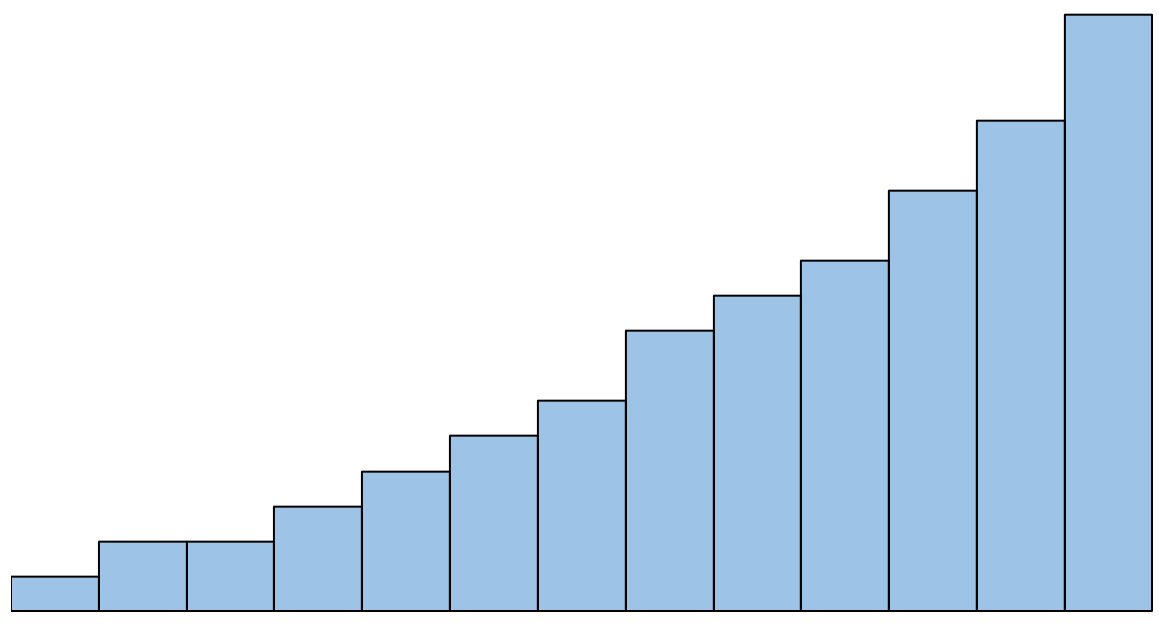
Wat te doen als deze veronderstelling niet wordt gerespecteerd

Als deze aanname wordt geschonden, kunnen we een Wilcoxon-test met ondertekende rang uitvoeren, die wordt beschouwd als het niet-parametrische equivalent van de t-test van gepaarde monsters en er niet van uitgaat dat de gepaarde verschillen normaal verdeeld zijn.

Hypothese 3: geen extreme uitschieters

Bij een paired samples t-test wordt ervan uitgegaan dat er geen extreme uitschieters in de gegevens voorkomen.

Hoe deze hypothese te verifiëren

De eenvoudigste manier om deze hypothese te testen is door een boxplot van gepaarde verschillen te maken en visueel te controleren of er uitschieters zijn.

Stel bijvoorbeeld dat de boxplot van gepaarde verschillen er als volgt uitziet:

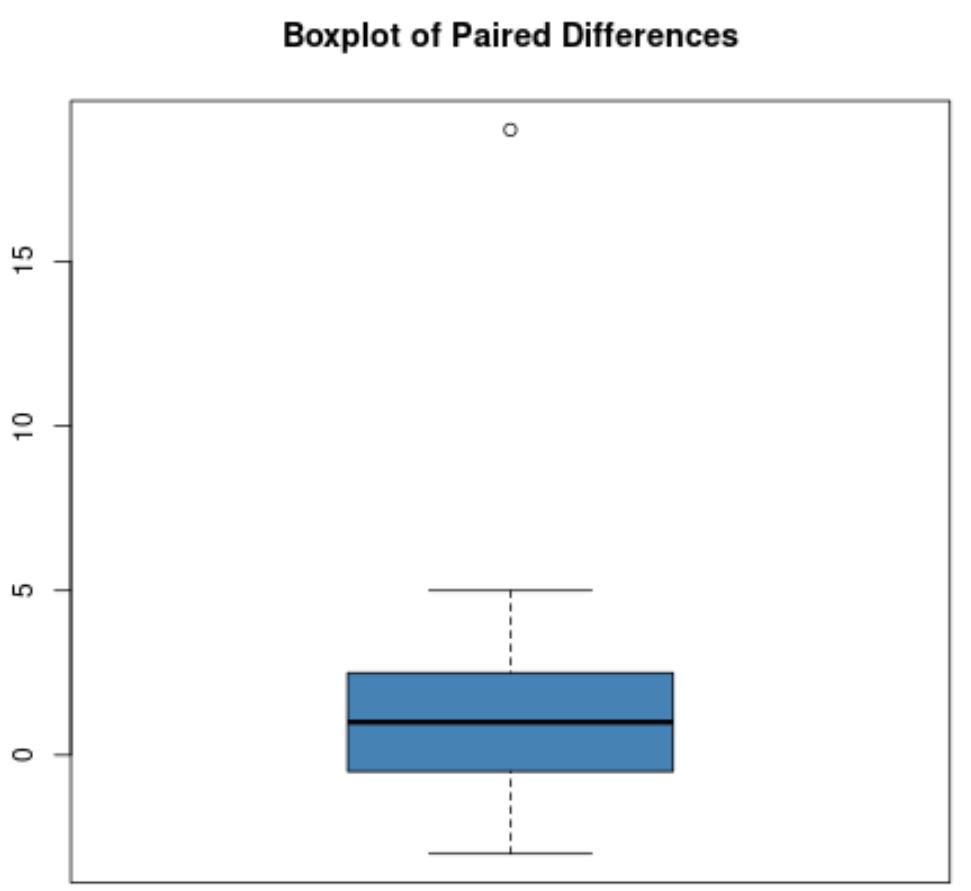
De meeste gepaarde verschillen liggen dicht bij nul, maar er is één gepaard verschil gelijk aan ongeveer 19, wat duidelijk een uitschieter is.

Opmerking : In een boxplot wordt doorgaans een cirkel gebruikt om een uitschieter aan te duiden.

Stel echter dat de boxplot van gepaarde verschillen er als volgt uitziet:

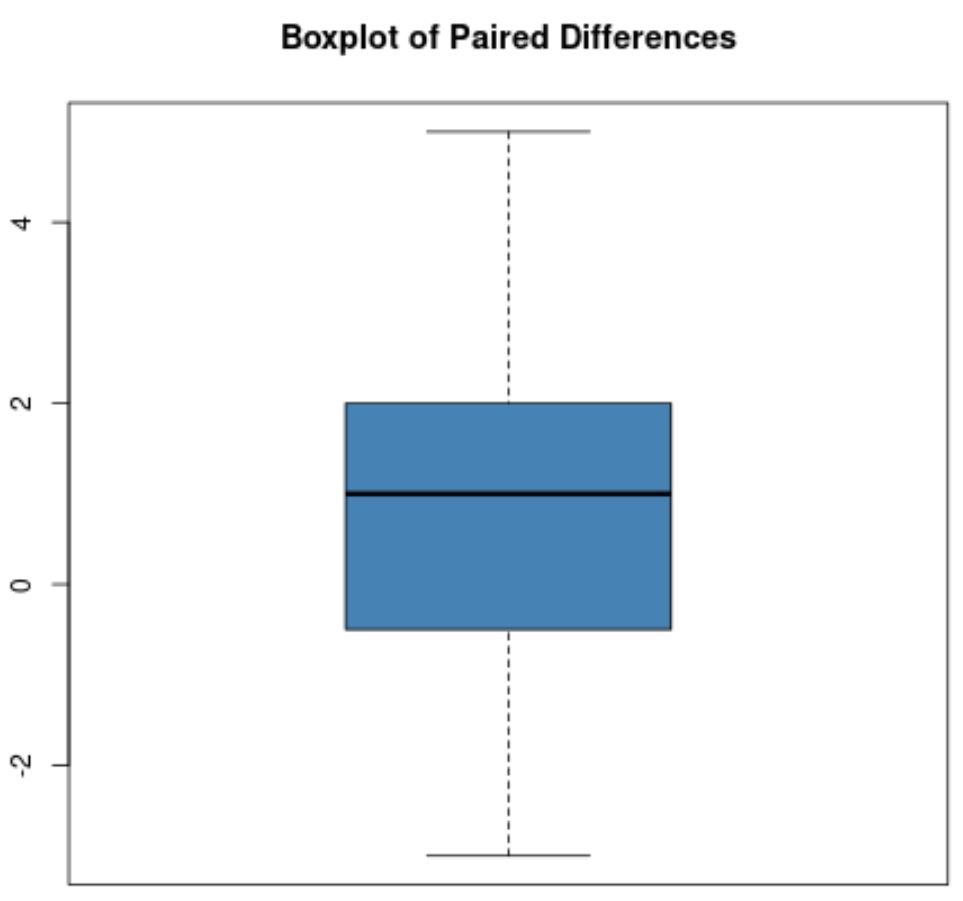
Er zijn geen duidelijke uitschieters in deze boxplot, dus we gaan ervan uit dat er geen extreme uitschieters in de gegevens voorkomen.

Wat te doen als deze veronderstelling niet wordt gerespecteerd

Als deze aanname wordt geschonden, kunnen de resultaten van de t-test van gepaarde monsters abnormaal worden beïnvloed door de uitbijter.

In dit scenario kunt u de uitbijter verwijderen als u denkt dat deze een foutief gegevenspunt vertegenwoordigt of het gevolg is van een gegevensinvoerfout.

Als alternatief kunt u de uitbijter behouden en deze eenvoudigweg noteren bij het rapporteren van de t-testresultaten met gepaarde steekproeven.

Aanvullende bronnen

In de volgende tutorials worden aannames uitgelegd die in andere statistische tests zijn gemaakt:

De vier hypothesen geformuleerd in een t-toets
De vier hypothesen van een chikwadraattoets
De vier hypothesen van parametrische tests