Gepaarde of ongepaarde t-test: wat is het verschil?

In de statistiek zijn er twee soorten t-tests met twee steekproeven :

Gepaarde t-test: wordt gebruikt om de gemiddelden van twee monsters te vergelijken wanneer elk individu in het ene monster ook in het andere monster voorkomt.

Ongepaarde t-test: wordt gebruikt om de gemiddelden van twee steekproeven te vergelijken wanneer elk individu in het ene monster onafhankelijk is van elk individu in het andere monster.

Opmerking: een ongepaarde t-test wordt gewoonlijk een independent samples t-test genoemd.

Stel bijvoorbeeld dat een hoogleraar wil vaststellen of twee verschillende studietechnieken al dan niet tot verschillende gemiddelde examenscores leiden.

Om een gepaarde t-test uit te voeren, zou hij 10 studenten kunnen rekruteren en ze een maand lang één studietechniek laten gebruiken en een examen kunnen afleggen, en ze vervolgens een maand lang de tweede studietechniek laten gebruiken en nog een examen van gelijke moeilijkheidsgraad kunnen afleggen.

Dit is hoe de gegevens eruit zouden zien:

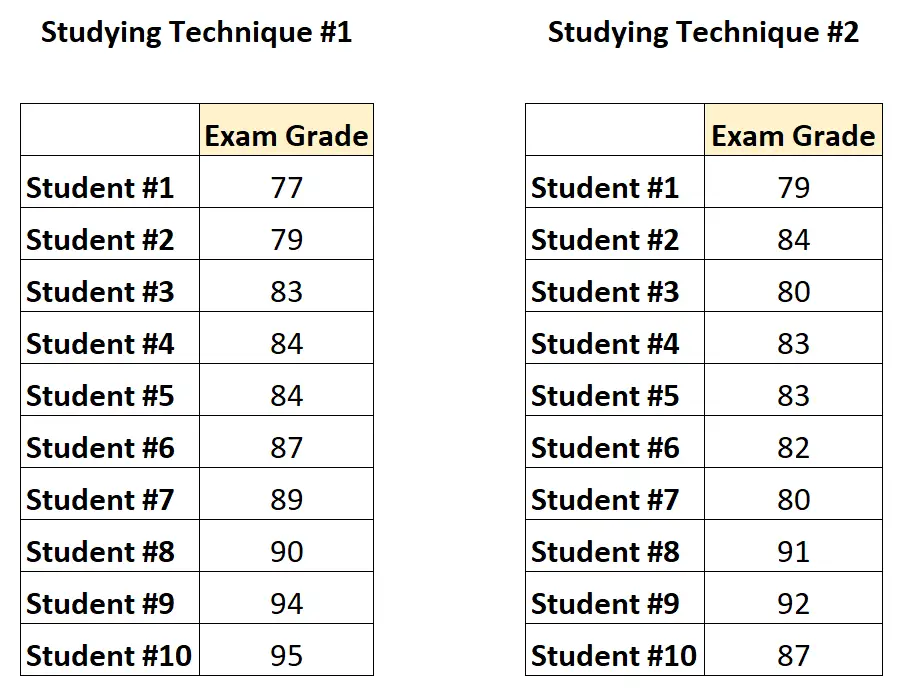
Omdat elke student in elke groep voorkomt, voerde de professor een gepaarde t-test uit om te bepalen of de gemiddelde scores tussen de twee groepen verschillend waren.

Om een ongepaarde t-test uit te voeren, zou hij in totaal twintig studenten kunnen rekruteren en deze willekeurig in twee groepen van tien kunnen verdelen. Hij zou de ene groep kunnen vragen een maand lang een studietechniek te gebruiken en de andere groep ‚de tweede studietechniek te gebruiken voor een maand. maand en laat alle studenten hetzelfde examen afleggen.

Dit is hoe de gegevens eruit zouden zien:

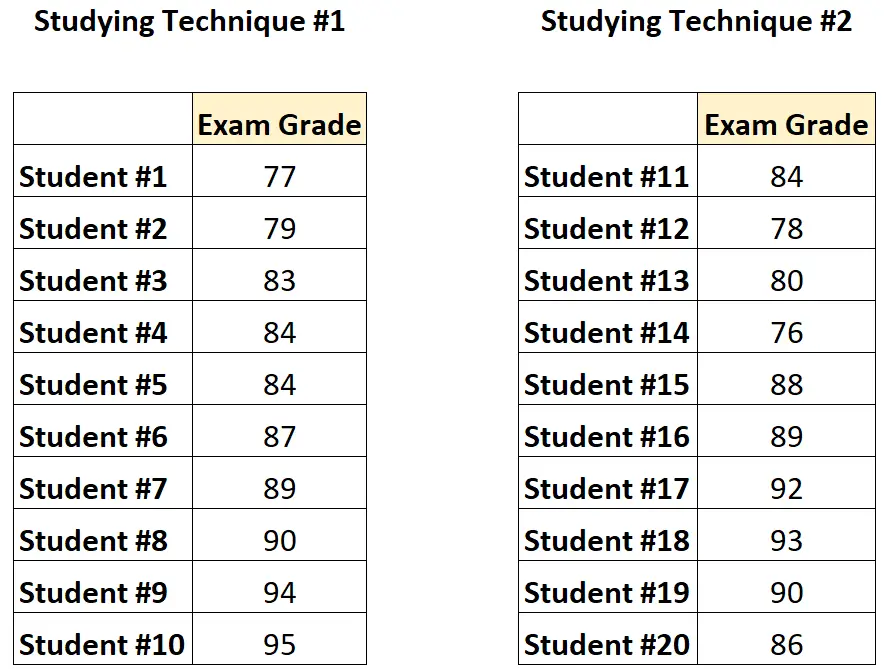
Omdat de studenten in de ene groep volledig onafhankelijk zijn van de studenten in de andere groep, zou de professor een ongepaarde t-test uitvoeren om te bepalen of de gemiddelde scores tussen de twee groepen verschillend zijn.

Hypotheses

Zowel gepaarde als ongepaarde t-tests gaan uit van de volgende aannames:

• Gegevens van beide monsters zijn verkregen met behulp van een willekeurige steekproefmethode .
• De gegevens van beide steekproeven moeten bij benadering normaal verdeeld zijn.
• Er mogen in geen van beide steekproeven extreme uitschieters voorkomen.

Deze aannames moeten worden geverifieerd voordat een t-test wordt uitgevoerd om de betrouwbaarheid van de testresultaten te garanderen.

Voor-en nadelen

De gepaarde t-test biedt de volgende voordelen :

• Er is een kleiner monster nodig. Merk op dat voor de gepaarde t-test in het vorige voorbeeld in totaal slechts 10 studenten nodig waren, terwijl voor de ongepaarde t-test in totaal 20 studenten nodig waren.
• Elk monster bevat individuen met dezelfde kenmerken. Beide groepen beschikken gegarandeerd over individuen met capaciteiten, intellect, enz. gelijk omdat in elke groep dezelfde individuen voorkomen.

Een gepaarde t-test heeft echter de volgende potentiële nadelen :

• Het potentieel voor verkleining van de steekproefomvang. Als een individu uit het onderzoek stapt, wordt de steekproefomvang van elke groep met één verkleind, aangezien dat individu in elke groep voorkomt.
• Het potentieel voor orde-effecten. Volgorde-effecten verwijzen naar verschillen in uitkomsten tussen de twee groepen als gevolg van de volgorde waarin de behandelingen aan individuen werden gepresenteerd. Een persoon kan bijvoorbeeld beter presteren op het tweede examen simpelweg omdat hij of zij zijn vaardigheden bij het afleggen van examens heeft verbeterd, en niet zozeer vanwege zijn studietechniek.

Houd deze voor- en nadelen in gedachten bij de beslissing of u een gepaarde of ongepaarde t-test wilt gebruiken.

Aanvullende bronnen

Bekijk de volgende tutorials om gepaarde t-tests beter te begrijpen:

• Een inleiding tot de t-test van gepaarde monsters
• Een t-test met gepaarde monsters uitvoeren in Excel

En gebruik de volgende tutorials om ongepaarde t-tests (ook wel independent samples t-tests genoemd) beter te begrijpen:

• Een inleiding tot de t-toets met twee steekproeven
• Een t-test met twee steekproeven uitvoeren in Excel