Wat zijn gestandaardiseerde residuen?

Een residu is het verschil tussen een waargenomen waarde en een voorspelde waarde in eenregressiemodel .

Het wordt als volgt berekend:

Residueel = Waargenomen waarde – Voorspelde waarde

Als we de waargenomen waarden uitzetten en de aangepaste regressielijn over elkaar leggen, zijn de residuen voor elke waarneming de verticale afstand tussen de waarneming en de regressielijn:

Eén type residu dat we vaak gebruiken om uitschieters in een regressiemodel te identificeren, wordt een gestandaardiseerd residu genoemd.

Het wordt als volgt berekend:

r _ik = e _ik / s(e _ik ) = e _ik / RSE√ 1-h _ii

Goud:

• e _i : het i- ^de residu
• RSE: de resterende standaardfout van het model
• h _ii : De opkomst van de ^ide waarneming

In de praktijk beschouwen we vaak elk gestandaardiseerd residu waarvan de absolute waarde groter is dan 3 als een uitbijter.

Dit betekent niet noodzakelijkerwijs dat we deze waarnemingen uit het model zullen verwijderen, maar we moeten ze in ieder geval verder bestuderen om te verifiëren dat ze niet het resultaat zijn van een gegevensinvoerfout of een andere vreemde gebeurtenis.

Let op: Soms worden gestandaardiseerde residuen ook wel ‘intern bestudeerde residuen’ genoemd.

Voorbeeld: Hoe gestandaardiseerde residuen berekenen

Stel dat we de volgende dataset hebben met in totaal 12 waarnemingen:

Als we statistische software (zoals R , Excel , Python , Stata , etc.) gebruiken om een lineaire regressielijn in deze dataset te passen, zullen we ontdekken dat de beste passende lijn blijkt te zijn:

y = 29,63 + 0,7553x

Met behulp van deze lijn kunnen we de voorspelde waarde voor elke Y-waarde berekenen op basis van de waarde van X. De voorspelde waarde van de eerste waarneming zou bijvoorbeeld zijn:

j = 29,63 + 0,7553*(8) = 35,67

We kunnen dan het residu voor deze waarneming als volgt berekenen:

Residueel = Waargenomen waarde – Voorspelde waarde = 41 – 35,67 = 5,33

We kunnen dit proces herhalen om het residu voor elke waarneming te vinden:

We kunnen ook statistische software gebruiken om te ontdekken dat de resterende standaardfout van het model 4,44 is.

En hoewel dit buiten het bestek van deze tutorial valt, kunnen we software gebruiken om de hefboomstatistiek (h _ii ) voor elke waarneming te vinden:

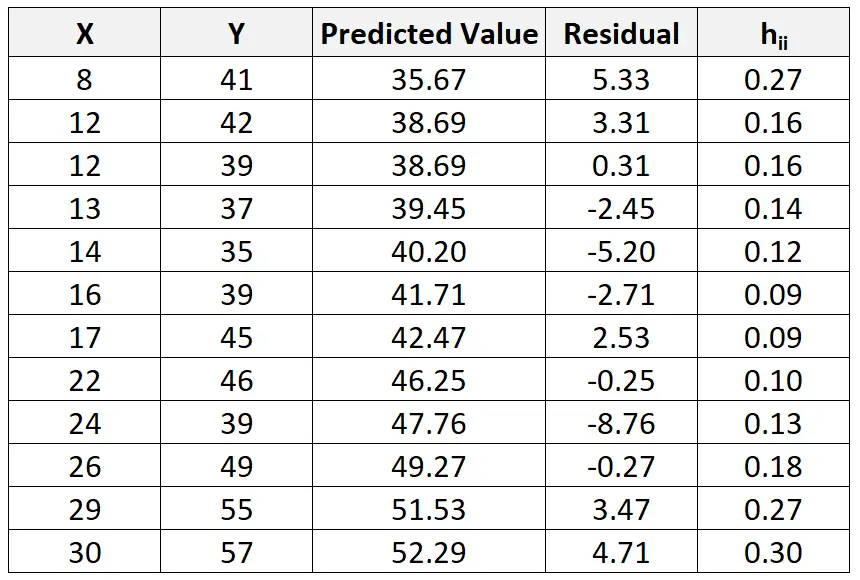
We kunnen dan de volgende formule gebruiken om het gestandaardiseerde residu voor elke waarneming te berekenen:

r _ik = e _i / RSE√ 1-h _ii

Het gestandaardiseerde residu voor de eerste waarneming wordt bijvoorbeeld als volgt berekend:

r _ik = 5,33 / 4,44√ 1-0,27 = 1,404

We kunnen dit proces herhalen om het gestandaardiseerde residu voor elke waarneming te vinden:

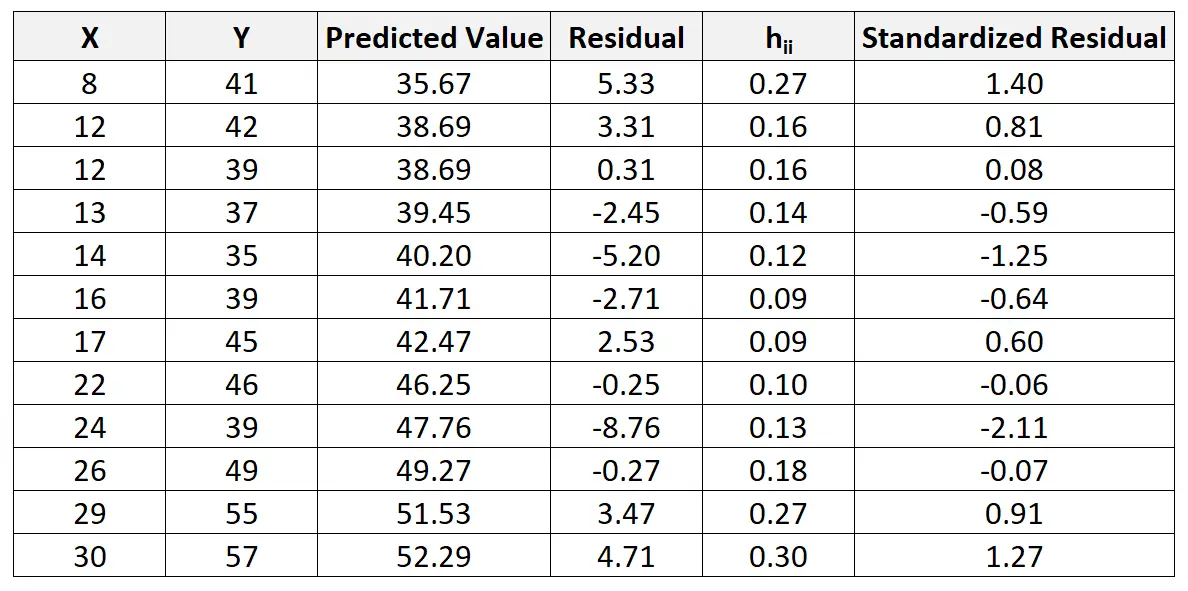
We kunnen dan een snel spreidingsdiagram maken van de voorspellende waarden tegen de gestandaardiseerde residuen om visueel te zien of een van de gestandaardiseerde residuen een absolute waardedrempel van 3 overschrijdt:

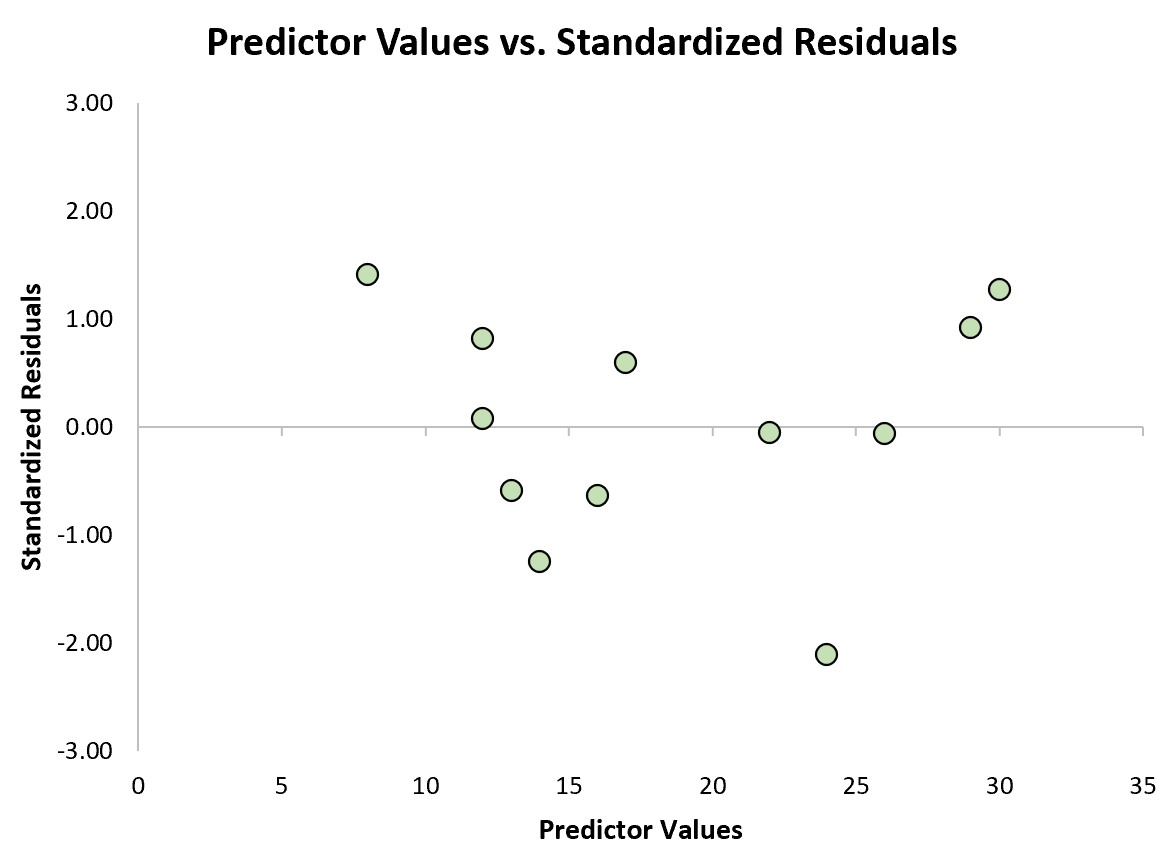
Uit de grafiek kunnen we zien dat geen van de gestandaardiseerde residuen een absolute waarde van 3 overschrijdt. Geen van de waarnemingen lijkt dus uitschieters te zijn.

Opgemerkt moet worden dat onderzoekers in sommige gevallen waarnemingen waarvan de gestandaardiseerde residuen een absolute waarde van 2 overschrijden, als uitschieters beschouwen.

Het is aan jou, afhankelijk van het vakgebied waarin je werkt en het specifieke probleem waaraan je werkt, of je een absolute waarde van 2 of 3 wilt gebruiken als drempel voor uitschieters.

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over gestandaardiseerde residuen:

Wat zijn residuen in de statistiek?
Hoe gestandaardiseerde residuen in Excel te berekenen
Hoe gestandaardiseerde residuen in R te berekenen
Hoe gestandaardiseerde residuen in Python te berekenen