Wat is een gestandaardiseerde teststatistiek?

Een statistische hypothese is een aanname over een populatieparameter . We kunnen bijvoorbeeld aannemen dat de gemiddelde lengte van een man in de Verenigde Staten 70 inch is. De hypothese met betrekking tot lengte is de statistische hypothese en de werkelijke gemiddelde lengte van een man in de Verenigde Staten is de populatieparameter .

Een hypothesetest is een formele statistische test die we gebruiken om een statistische hypothese al dan niet te verwerpen.

Het basisproces voor het testen van hypothesen is als volgt:

1. Verzamel voorbeeldgegevens.

2. Bereken de gestandaardiseerde teststatistiek voor de voorbeeldgegevens.

3. Vergelijk de gestandaardiseerde teststatistiek met een kritische waarde. Als deze extremer is dan de kritische waarde, verwerp dan de nulhypothese. Anders verwerpt u de nulhypothesetest niet.

De formule die we gebruiken om de gestandaardiseerde teststatistiek te berekenen, varieert afhankelijk van het type hypothesetest dat we uitvoeren.

De volgende tabel toont de formule die moet worden gebruikt om de gestandaardiseerde teststatistiek te berekenen voor elk van de vier hoofdtypen hypothesetoetsen:

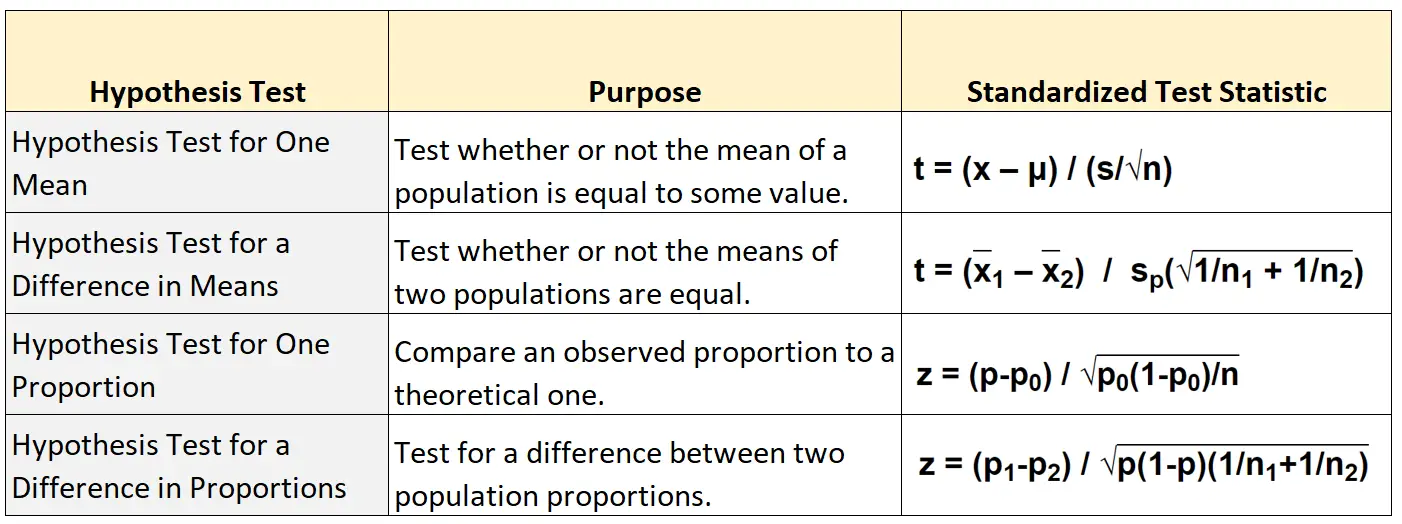
Hypothese testen voor een gemiddelde

Een one-sample t-test wordt gebruikt om te testen of het gemiddelde van een populatie gelijk is aan een bepaalde waarde.

De gestandaardiseerde teststatistiek voor dit type test wordt als volgt berekend:

t = ( X – μ) / (s/√n)

Goud:

• x: steekproefgemiddelden
• μ ₀ : hypothetisch populatiegemiddelde
• s: standaardafwijking van het monster
• n: steekproefomvang

Raadpleeg deze tutorial voor een voorbeeld van het berekenen van deze gestandaardiseerde teststatistiek.

Hypothesetesten voor een verschil in gemiddelden

Een t-test met twee steekproeven wordt gebruikt om te testen of de gemiddelden van twee populaties gelijk zijn of niet.

De gestandaardiseerde teststatistiek voor dit type test wordt als volgt berekend:

t = ( X ₁ – X ₂ ) / s _p (√ 1/n ₁ + 1/n ₂ )

waarbij x ₁ en x ₂ de steekproefgemiddelden zijn, n ₁ en n ₂ de steekproefomvang zijn, en waarbij _sp als volgt wordt berekend:

s _p = √ (n ₁ -1)s ₁ ² + (n ₂ -1)s ₂ ² / (n ₁ +n ₂ -2)

waarbij s ₁ ² en s ₂ ² de steekproefvarianties zijn.

Raadpleeg deze tutorial voor een voorbeeld van het berekenen van deze gestandaardiseerde teststatistiek.

Hypothesetesten voor een deel

Een z-test met één proportie wordt gebruikt om een waargenomen proportie te vergelijken met een theoretisch proportie.

De gestandaardiseerde teststatistiek voor dit type test wordt als volgt berekend:

z = (pp ₀ ) / √ p ₀ (1-p ₀ )/n

Goud:

• p: waargenomen monsteraandeel
• p ₀ : hypothetisch aandeel van de bevolking
• n: steekproefomvang

Raadpleegdeze tutorial voor een voorbeeld van het berekenen van deze gestandaardiseerde teststatistiek.

Hypothesetesten voor een verschil in verhoudingen

Een z-test met twee proporties wordt gebruikt om te testen op een verschil tussen twee populatieproporties.

De gestandaardiseerde teststatistiek voor dit type test wordt als volgt berekend:

z = (p ₁ -p ₂ ) / √ p(1-p)(1/n ₁ +1/n ₂ )

waarbij p ₁ en p ₂ de steekproefverhoudingen zijn, n ₁ en n ₂ de steekproefomvang zijn, en waarbij p het totale gepoolde aandeel is, als volgt berekend:

p = (p ₁ n ₁ + p ₂ n ₂ )/(n ₁ + n ₂ )

Raadpleeg deze tutorial voor een voorbeeld van het berekenen van deze gestandaardiseerde teststatistiek.