Gestratificeerde steekproef
In dit artikel leggen we uit wat gestratificeerde steekproeven zijn en hoe deze worden uitgevoerd. Hier vindt u uitleg over de subtypen van gestratificeerde steekproeven en tot slot wat de voor- en nadelen van gestratificeerde steekproeven zijn.
Wat is gestratificeerde steekproeftrekking?
Gestratificeerde steekproeven zijn een statistische methode die wordt gebruikt om elementen van een steekproef te selecteren door de populatie in groepen te verdelen (strata genoemd). Dat wil zeggen dat bij gestratificeerde steekproeven de populatie in strata wordt verdeeld en dat individuen uit elk stratum willekeurig worden geselecteerd om de gehele onderzoekssteekproef te vormen.
Strata zijn homogene groepen, of met andere woorden, individuen in een laag hebben hun eigen kenmerken die hen onderscheiden van andere lagen. Een individu kan dus maar tot één stratum behoren.
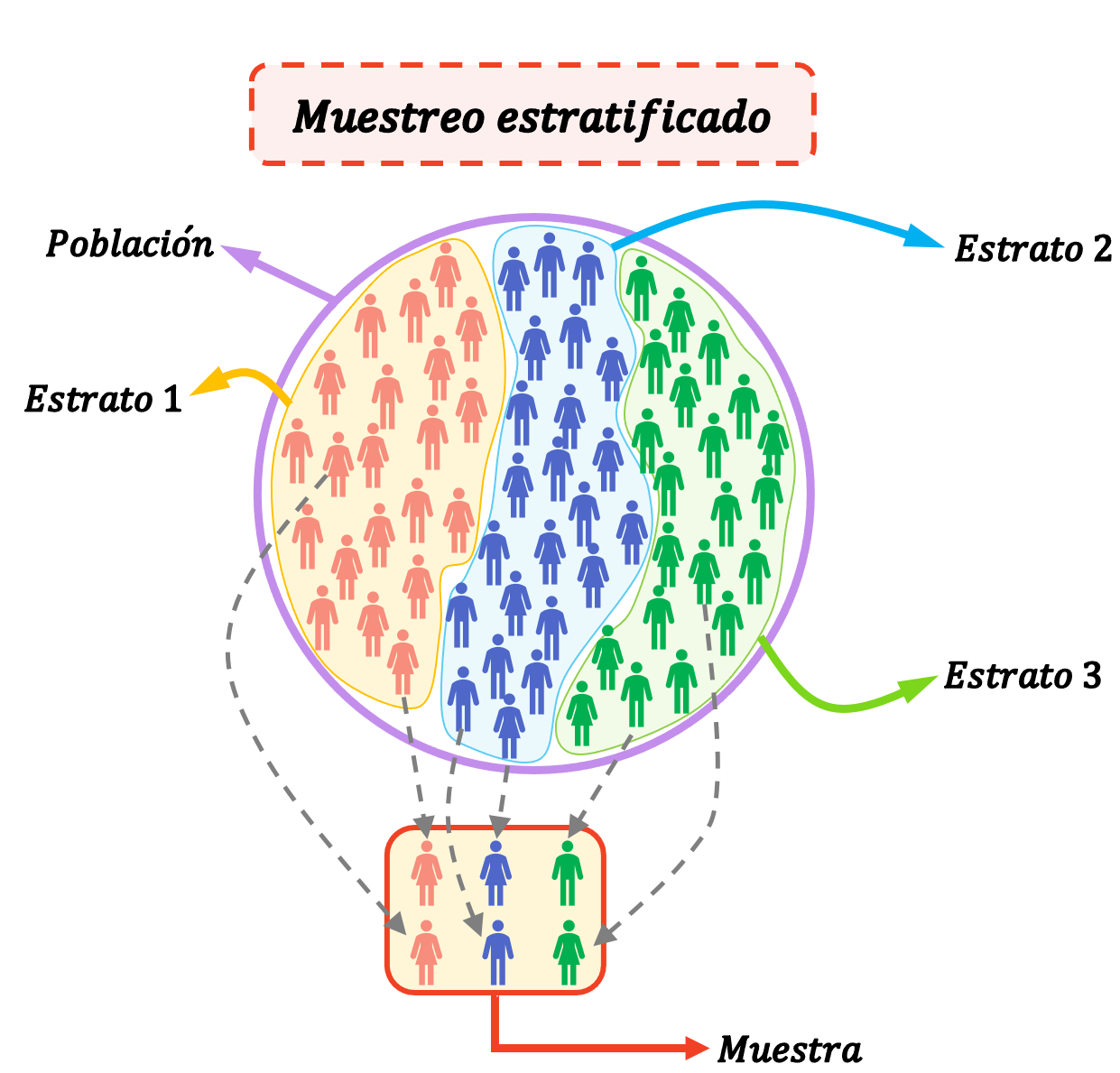
Gestratificeerde steekproeven zijn erg handig als de populatie bestaat uit zeer homogene groepen die sterk van elkaar verschillen.
Logischerwijs geeft de som van de omvang van alle strata de omvang van de statistische populatie:
![]()
Op dezelfde manier is de som van de in elk stratum gekozen steekproefomvang gelijk aan de totale steekproefomvang van het statistische onderzoek:
![]()
Over het algemeen maken we onderscheid tussen hoofdletters en kleine letters om respectievelijk de populatie of de steekproef aan te duiden.
Hoe gestratificeerde steekproeven te doen
De stappen voor het uitvoeren van gestratificeerde steekproeven zijn als volgt:
- Definieer de doelgroep.
- Kies de variabele stratificatie en hoeveel strata er zullen zijn.
- Identificeer tot welke laag elk element van de bevolking behoort.
- Bereken de omvang van elk stratum dat deel zal uitmaken van de steekproef.
- Selecteer willekeurig de elementen uit elk stratum die tot de onderzoekssteekproef zullen behoren. Voor elk stratum moeten evenveel elementen worden geselecteerd als in de vorige stap is besloten.
Houd er rekening mee dat de omvang van elk stratum in de steekproef niet alleen afhangt van de omvang van het stratum, maar ook van het type gestratificeerde steekproef. Vervolgens wordt elk type gestratificeerde steekproef uitgelegd en hoe de steekproefomvang van elk stratum wordt berekend aan de hand van een voorbeeld.
Soorten gestratificeerde bemonstering
Nu u de definitie van gestratificeerde steekproeven kent, moet u weten dat er verschillende soorten gestratificeerde steekproeven bestaan, die als volgt worden geclassificeerd:
- Proportionele gestratificeerde steekproeven
- Uniforme gestratificeerde bemonstering
- De monsterneming is optimaal
Elk type gestratificeerde steekproeftrekking wordt hieronder in detail uitgelegd om de betekenis ervan beter te begrijpen.
Proportionele gestratificeerde steekproeven
Bij gestratificeerde proportionele steekproeven , of proportionele toewijzingssteekproeven, is het aantal elementen uit elk stratum dat deel uitmaakt van de onderzoekssteekproef evenredig met de omvang van elk stratum.
Als de ene laag dus groter is dan de andere, zal de uiteindelijke steekproef meer elementen uit die laag bevatten. Aan de andere kant, als het ene stratum kleiner is dan het andere, zullen er minder elementen uit dit stratum in de statistische analysesteekproef aanwezig zijn.
Dit type gestratificeerde steekproeftrekking is nuttig wanneer de strata verschillende groottes hebben en we willen dat de steekproef meer elementen uit de grotere strata omvat.
Om het aantal elementen uit elk stratum te berekenen dat in de steekproef zal zitten, moet de omvang van elk stratum worden gedeeld door de som van de maten van alle strata. Het resultaat is het deel van het stratum dat in de steekproef moet worden opgenomen. Dit moet dus worden vermenigvuldigd met de gewenste steekproefomvang.
![]()
Goud
![]()
is de gewenste totale steekproefomvang,
![]()
het aantal elementen in de laag
![]()
in het monster worden opgenomen,
![]()
stratumgrootte
![]()
, En
![]()
het totale aantal elementen in de populatie.
Stel je bijvoorbeeld voor dat we een onderzoek willen doen in een bedrijf met 150 werknemers, waarbij we een steekproef van 50 mensen nemen en de gegevens stratificeren op basis van de leeftijd van de werknemers. We kunnen de gegevens als volgt classificeren:
- Van 20 tot 29 jaar: 35 werknemers
- Van 30 tot 39 jaar: 57 medewerkers
- Van 40 tot 49 jaar: 42 medewerkers
- Van 50 tot 59 jaar: 16 medewerkers
Als we de gegevens dus proportioneel stratificeren, zal de steekproef er als volgt uitzien:
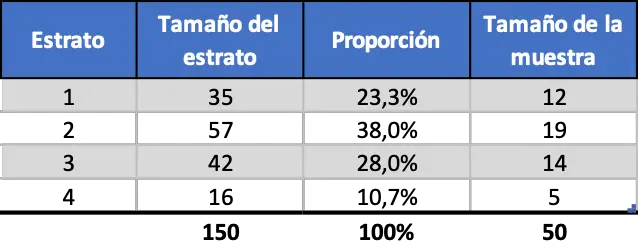
Uniforme gestratificeerde bemonstering
Bij uniforme gestratificeerde steekproeven , of uniforme bevestigingssteekproeven, is het aantal elementen uit elk stratum dat deel uitmaakt van de onderzoekssteekproef gelijk.
Bij dit soort steekproeven heeft dus elk stratum hetzelfde gewicht. Ongeacht of een stratum meer of minder individuen heeft dan een andere stratum, ze zullen allemaal in de steekproef vertegenwoordigd zijn door hetzelfde aantal individuen.
In dit geval moet, om de omvang van de elementen in elk stratum te berekenen, de gewenste steekproefomvang worden gedeeld door het aantal bestaande strata. Met andere woorden, de volgende formule moet worden gebruikt:
![]()
Goud
![]()
is de gewenste totale steekproefomvang,
![]()
het aantal elementen in de laag
![]()
wie in de steekproef zal worden opgenomen, en
![]()
het aantal lagen waarin de bevolking is verdeeld.
In navolging van het vorige voorbeeld zal de steekproefomvang van elk stratum, aangezien we een steekproef van 50 werknemers wilden en er in totaal vier verschillende strata waren, als volgt zijn:
![]()
Omdat het resultaat een decimaal getal is, zullen sommige strata 12 werknemers hebben en andere 13, totdat ze 50 werknemers bereiken. De uniforme gestratificeerde steekproef is dus als volgt:
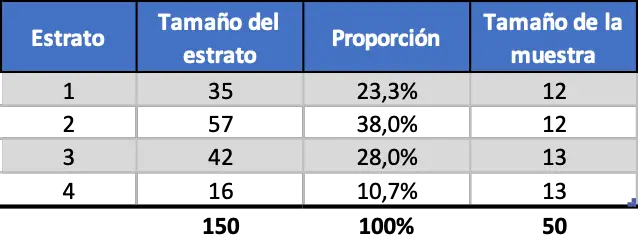
Zoals u kunt zien, is de steekproefomvang van elk stratum onafhankelijk van het aandeel van elk stratum.
Optimale gestratificeerde bemonstering
Bij optimale gestratificeerde steekproeven hangt het aantal elementen in elk stratum proportioneel af van de variabiliteit van elk stratum.
Straten met een grotere variabiliteit zullen dus een grotere steekproefomvang hebben, en omgekeerd zullen strata met minder variabiliteit een kleinere steekproefomvang hebben.
De formule om te bepalen hoeveel elementen uit elk stratum deel zullen uitmaken van de statistische onderzoekssteekproef is als volgt:
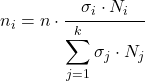
Goud
![]()
is de gewenste totale steekproefomvang,
![]()
is het aantal elementen in de laag
![]()
in het monster worden opgenomen,
![]()
is de standaardafwijking (of typische afwijking) van het stratum
![]()
, En
![]()
is de grootte van de laag
![]()
.
Voor- en nadelen van gestratificeerde bemonstering
Gestratificeerde steekproeven hebben de volgende voor- en nadelen:
| voordeel | Nadelen |
|---|---|
| Het maakt het mogelijk om niet alleen de gehele populatie, maar ook elke specifieke laag statistisch te bestuderen. | Dit is een ingewikkelde bemonsteringsmethode om te implementeren. |
| De steekproeffout die wordt begaan door gestratificeerde steekproeven is altijd gelijk aan of kleiner dan die van eenvoudige willekeurige steekproeven. | Dit is een tijdrovend en daardoor duur bemonsteringsproces. |
| Hiermee kunt u profiteren van de kennis van de onderzoeker over de populatie. | Er is veel informatie nodig over het geanalyseerde monster om het te kunnen stratificeren. |
| Bij gestratificeerde steekproeven zorgen we ervoor dat ten minste één element uit elk stratum in de steekproef wordt opgenomen. | Om steekproeven te kunnen uitvoeren, is het noodzakelijk om het aandeel van elk stratum te kennen. |
Het belangrijkste kenmerk van gestratificeerde steekproeven is dat deze worden gebruikt om elke groep of laag waarin de populatie is verdeeld statistisch te analyseren. Uiteraard kan met dit soort steekproeven ook de gehele populatie worden bestudeerd. Bovendien zullen de voordelen van gegevensstratificatie groter zijn als de strata van elkaar verschillen.
Integendeel, het feit dat de gegevens worden gestratificeerd om de steekproeven te kunnen uitvoeren, impliceert een toename van de complexiteit van de steekproeven, waarbij gestratificeerde steekproeven ingewikkelder zijn om uit te voeren vergeleken met andere soorten steekproeven. Deze eigenschap impliceert ook dat het een duur monster is om te maken, omdat het tijd kost om de stratificatie correct uit te voeren.
Een ander nadeel van gestratificeerde steekproeven is dat er veel informatie nodig is over de populatie die men wil bestuderen, wat niet nodig is bij andere soorten steekproeven, zoals eenvoudige willekeurige steekproeven. Hoewel dit nadeel kan worden verzacht als de onderzoeker over grote kennis op dit gebied beschikt.
Ten slotte verkrijgen we bij gestratificeerde steekproeven een steekproef die representatiever is voor de populatie dan bij andere soorten steekproeven, omdat we ervoor zorgen dat elementen uit elk stratum worden opgenomen. In andere monsters daarentegen mag het resulterende monster geen elementen uit welk stratum dan ook bevatten.