Hoe gestudentiseerde residuen in python te berekenen

Een studentenresidu is eenvoudigweg een residu gedeeld door de geschatte standaarddeviatie.

In de praktijk zeggen we over het algemeen dat elke waarneming in een dataset waarvan het studentenresidu groter is dan de absolute waarde van 3, een uitbijter is.

We kunnen snel de door studenten verkregen residuen van een regressiemodel in Python verkrijgen met behulp van de functie OLSResults.outlier_test() van statsmodels, die de volgende syntaxis gebruikt:

OLSResults.outlier_test()

waarbij OLSResults de naam is van een lineair model dat past met behulp van de statsmodels ols() functie.

Voorbeeld: berekening van gestudentiseerde residuen in Python

Stel dat we het volgende eenvoudige lineaire regressiemodel in Python bouwen:

 #import necessary packages and functions
import numpy as np
import pandas as pd
import statsmodels. api as sm
from statsmodels. formula . api import ols

#create dataset
df = pd. DataFrame ({'rating': [90, 85, 82, 88, 94, 90, 76, 75, 87, 86],
                   'points': [25, 20, 14, 16, 27, 20, 12, 15, 14, 19]})

#fit simple linear regression model
model = ols('rating ~ points', data=df). fit ()

We kunnen de functie outlier_test() gebruiken om een DataFrame te produceren dat de studentized residuen bevat voor elke observatie in de dataset:

 #calculate studentized residuals
stud_res = model. outlier_test ()

#display studentized residuals
print(stud_res)

    student_resid unadj_p bonf(p)
0 -0.486471 0.641494 1.000000
1 -0.491937 0.637814 1.000000
2 0.172006 0.868300 1.000000
3 1.287711 0.238781 1.000000
4 0.106923 0.917850 1.000000
5 0.748842 0.478355 1.000000
6 -0.968124 0.365234 1.000000
7 -2.409911 0.046780 0.467801
8 1.688046 0.135258 1.000000
9 -0.014163 0.989095 1.000000

Dit DataFrame geeft voor elke waarneming in de dataset de volgende waarden weer:

• Het gestudentiseerde residu
• De niet-gecorrigeerde p-waarde van het gestudentiseerde residu
• De door Bonferroni gecorrigeerde p-waarde van het studentenresidu

We kunnen zien dat het gestudentiseerde residu voor de eerste observatie in de dataset -0.486471 is, het gestudentiseerde residu voor de tweede observatie is -0.491937 , enzovoort.

We kunnen ook een snelle grafiek maken van de waarden van de voorspellende variabelen tegen de overeenkomstige gestudentiseerde residuen:

 import matplotlib. pyplot as plt

#define predictor variable values and studentized residuals
x = df[' points ']
y = stud_res[' student_resid ']

#create scatterplot of predictor variable vs. studentized residuals
plt. scatter (x,y)
plt. axhline (y=0, color=' black ', linestyle=' -- ')
plt. xlabel (' Points ')
plt. ylabel (' Studentized Residuals ') 

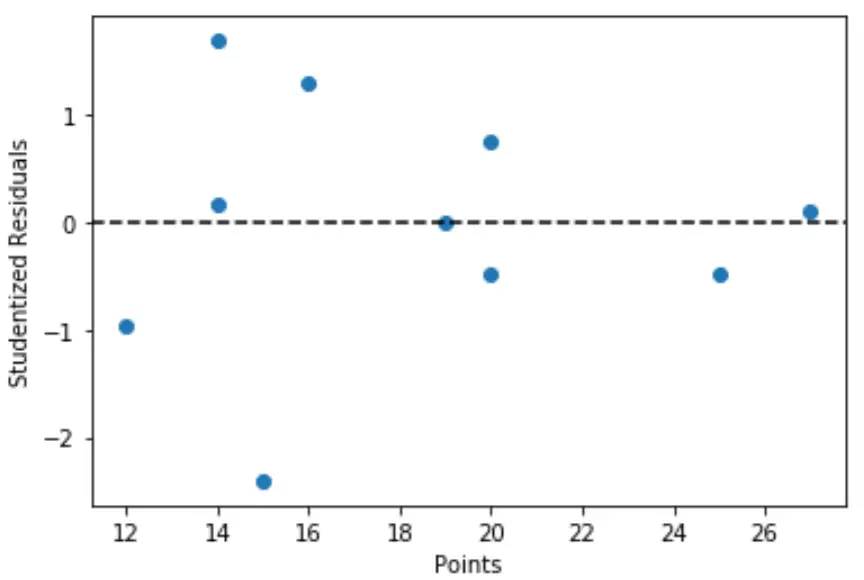
Uit de grafiek kunnen we zien dat geen van de waarnemingen een leerlingresidu heeft met een absolute waarde groter dan 3, dus er zijn geen duidelijke uitschieters in de dataset.

Aanvullende bronnen

Hoe eenvoudige lineaire regressie uit te voeren in Python
Hoe u meerdere lineaire regressies uitvoert in Python
Hoe u een restplot maakt in Python