Inferentie en voorspelling: wat is het verschil?

Vaak willen we in de statistiek gegevens gebruiken om een van de volgende twee redenen:

(1) Gevolgtrekking: we willen de aard van de relatie tussen de voorspellende variabelen en deresponsvariabele in een bestaande dataset begrijpen.

(2) Voorspelling: We willen een bestaande dataset gebruiken om een model te bouwen dat de waarde van de responsvariabele van een nieuwe waarneming voorspelt.

Stel dat we bijvoorbeeld de volgende dataset hebben met informatie over huizen:

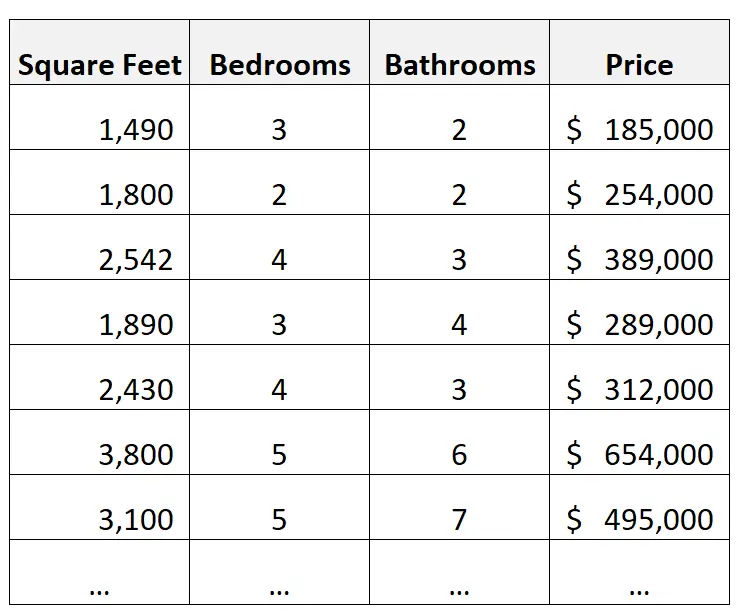
Een voorbeeld van gevolgtrekking:

Stel dat we een meervoudig lineair regressiemodel bouwen met vierkante meters, het aantal slaapkamers en het aantal badkamers als voorspellende variabelen en de prijs als responsvariabele.

We zouden dan de regressiecoëfficiënten kunnen gebruiken om de gemiddelde prijsverandering te begrijpen die gepaard gaat met een verandering van één eenheid in elk van de voorspellende variabelen.

We zouden bijvoorbeeld kunnen begrijpen hoeveel de prijs (gemiddeld) verandert met elke extra slaapkamer, elke extra badkamer en elke extra vierkante meter.

Een voorbeeld van een voorspelling:

We zouden hetzelfde meervoudige lineaire regressiemodel kunnen bouwen en dit kunnen gebruiken om de waarde van een nieuw huis te voorspellen op basis van de vierkante meters, het aantal slaapkamers en het aantal badkamers.

We kunnen het model bijvoorbeeld gebruiken om de prijs te voorspellen van een nieuw huis met 3 slaapkamers, 3 badkamers en 2.000 vierkante meter.

Vervolgens kunnen we onze voorspelling vergelijken met de daadwerkelijke verkoopprijs en beoordelen of het huis ondergewaardeerd of overgewaardeerd lijkt.

De volgende voorbeelden illustreren het verschil tussen gevolgtrekking en voorspelling in verschillende scenario’s:

Voorbeeld 1: gevolgtrekking en voorspelling in de sport

Stel dat we de volgende dataset hebben met informatie over professionele basketbalteams:

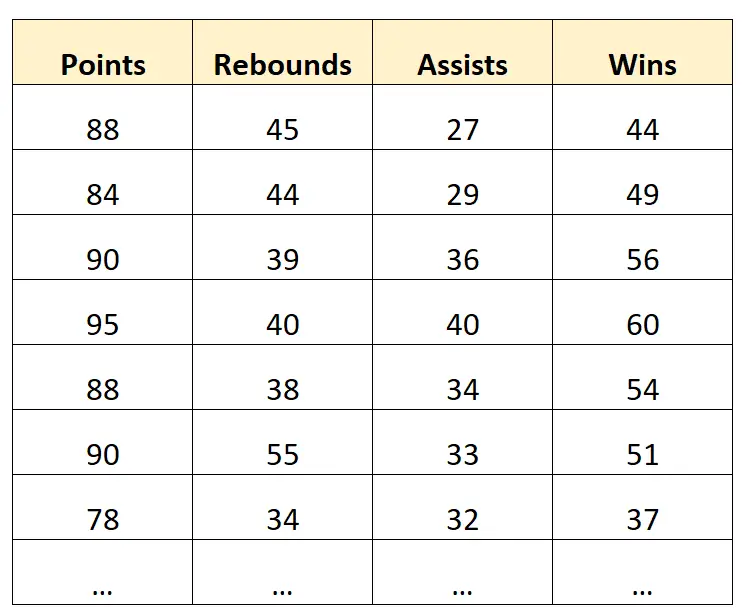
Een voorbeeld van gevolgtrekking:

Stel dat we een meervoudig lineair regressiemodel bouwen met punten, rebounds en assists als voorspellende variabelen en overwinningen als responsvariabele.

We zouden het model vervolgens kunnen gebruiken om te begrijpen hoeveel het aantal overwinningen (gemiddeld) verandert met elk extra punt, rebound en assist.

Een voorbeeld van een voorspelling:

We zouden hetzelfde meervoudige lineaire regressiemodel kunnen bouwen en gebruiken om te voorspellen hoeveel overwinningen een team zal behalen op basis van het aantal punten, rebounds en assists.

We kunnen het model bijvoorbeeld gebruiken om te voorspellen hoeveel overwinningen een team met 90 punten, 40 rebounds en 30 assists zal behalen.

Voorbeeld 2: gevolgtrekking en voorspelling in het bedrijfsleven

Stel dat we de volgende dataset hebben met informatie over de jaaromzet (in miljoenen) van verschillende bedrijven:

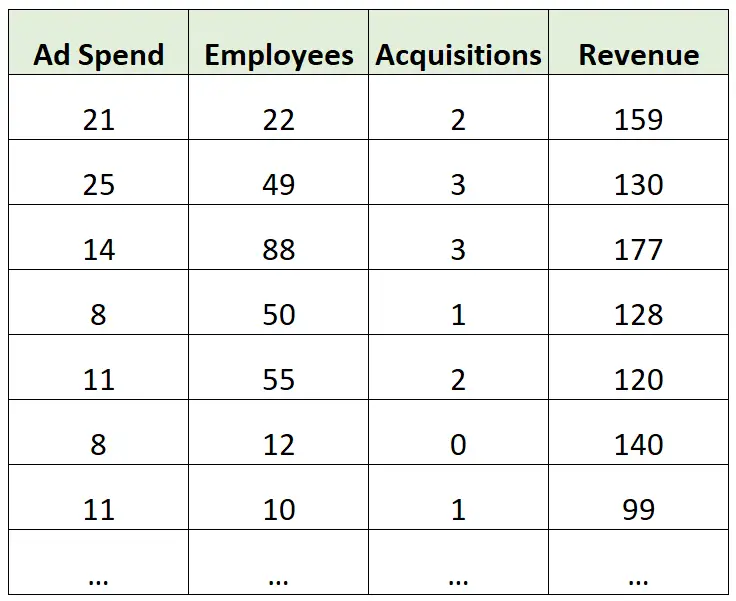
Een voorbeeld van gevolgtrekking:

Stel dat we een meervoudig lineair regressiemodel bouwen met advertentie-uitgaven, aantal werknemers en totale acquisities als voorspellende variabelen en de jaarlijkse omzet als responsvariabele.

We zouden het model vervolgens kunnen gebruiken om te begrijpen hoeveel de totale jaarlijkse omzet (gemiddeld) verandert met elke extra dollar die aan advertenties wordt besteed, elke extra werknemer en elke extra acquisitie.

Een voorbeeld van een voorspelling:

We zouden hetzelfde meervoudige lineaire regressiemodel kunnen bouwen en dit kunnen gebruiken om de jaarlijkse omzet van een bedrijf te voorspellen op basis van de totale marketinguitgaven, het aantal werknemers en het totale aantal acquisities.

We kunnen het model bijvoorbeeld gebruiken om de jaaromzet te voorspellen van een bedrijf dat 25 miljoen dollar uitgeeft aan advertenties, 40 werknemers heeft en twee overnames heeft gedaan.

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over belangrijke termen die u in de statistiek moet begrijpen:

Beschrijvende of inferentiële statistiek: wat is het verschil?
Meetniveaus: nominaal, ordinaal, interval en ratio
Kwalitatieve en kwantitatieve variabelen: wat is het verschil?