Gewogen gemiddelde

Von Dr.benjamin anderson August 6, 2023 Statistieken Keine Kommentare

Hier leggen we uit wat het gewogen gemiddelde is en hoe dit wordt berekend. U zult een opgeloste oefening kunnen zien over hoe we het gewogen gemiddelde vinden. En bovendien kunt u aan het einde met de rekenmachine het gewogen gemiddelde van elke dataset berekenen.

Wat is het gewogen gemiddelde?

Het gewogen gemiddelde is een maatstaf voor de centrale plaats van beschrijvende statistieken. Om het gewogen gemiddelde te berekenen, moet u eerst alle statistische gegevens vermenigvuldigen met het gewicht (of gewicht), vervolgens alle producten bij elkaar optellen en ten slotte de gewogen som delen door de som van alle gewichten.

Met andere woorden, de formule voor het gewogen gemiddelde is als volgt:

Waar x _i elk gegevensmonster vertegenwoordigt en _met het bijbehorende gewicht.

Dus hoe meer gewicht een gegeven heeft, hoe belangrijker het wordt bij de berekening van het gewogen gemiddelde. Met andere woorden: hoe hoger de weging van een gegeven, hoe meer dit het resultaat van het gewogen gemiddelde zal beïnvloeden.

Het gewogen gemiddelde is vooral handig voor het berekenen van cijfers, omdat je hiermee de oefeningen of examens die tijdens een cursus worden afgelegd, met verschillend belang kunt evalueren. Het gewogen gemiddelde wordt ook gebruikt om de CPI (Consumer Price Index) te berekenen, een indicator voor het meten van de prijzen van een bevolking.

Naast het gewogen gemiddelde zijn er ook andere soorten gemiddelden, zoals geometrisch gemiddelde, rekenkundig gemiddelde, kwadratisch gemiddelde en harmonisch gemiddelde.

Hoe het gewogen gemiddelde te berekenen

Om het gewogen gemiddelde te berekenen moeten de volgende stappen gevolgd worden:

Vermenigvuldig elke statistische gegevens met het overeenkomstige gewicht.
Tel alle producten op die in de vorige stap zijn berekend.
Deel de gewogen som hierboven door de som van alle gewichten.
Het verkregen resultaat is het gewogen gemiddelde van de statistische steekproef.

👉 U kunt de onderstaande rekenmachine gebruiken om het gewogen gemiddelde van elke dataset te berekenen.

Gewogen gemiddelde voorbeeld

Gezien de definitie van gewogen gemiddelde, zullen we nu een oefening oplossen om volledig te begrijpen hoe het gewogen gemiddelde uit een reeks gegevens wordt verkregen.

Een 1e jaars middelbare scholier behaalde voor het vak wiskunde de volgende cijfers: een 7 op het deelexamen dat voor 30% meetelt, een 9 op het groepswerk dat 20% waard is, een 6 op de oefeningen die in de les gegeven worden met een weging van 10% en een 8 op het eindexamen met een weging van 40%. Wat is je eindcijfer voor het vak?

Om het cijfer van de student te bepalen, moet je het gewogen gemiddelde vinden met de waarden die in de stelling worden gegeven. Om dit te doen, passen we de formule voor het gewogen gemiddelde toe:

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+x_3\cdot w_3+x_4\cdot w_4+x_5\cdot w_5}{w_1+w_2+w_3+w_4+w_5}$

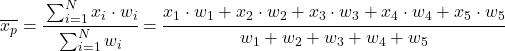
De score van elk resultaat is de statistische waarde en het percentage komt overeen met het gewicht van de genoemde waarde. Daarom vervangen we de waarden en gewichten in de formule en voeren we de gewogen gemiddelde berekening uit:

$\overline{x_p}=\cfrac{7\cdot 0,30+9\cdot 0,20+6\cdot 0,10+8\cdot 0,40}{0,30+0,20+0,10+0,40}=7,7$

Het wiskundeeindcijfer van deze leerling zal dus een 7,7 zijn, omdat dit het resultaat is dat is verkregen uit het gewogen gemiddelde.

Gewogen gemiddelde rekenmachine

Voer gegevens uit een statistische steekproef en hun respectievelijke gewichten in de onderstaande rekenmachine in om het gewogen gemiddelde te berekenen.

Voer de statistische gegevens in het eerste vak in en hun respectieve gewichten in het tweede vak. U moet de gewichten in dezelfde volgorde als de gegevens en in decimaal formaat schrijven. Alle getallen moeten worden gescheiden door een spatie en moeten worden ingevoerd met de punt als decimaal scheidingsteken.

Gestandaardiseerde gewichten

Zoals we hebben gezien, is het gewicht in het gewogen gemiddelde de waarde die aan elk gegeven wordt gegeven om er meer of minder belang aan te geven. Als informatie dus erg belangrijk is, zal deze een zeer groot gewicht hebben, maar als informatie niet erg relevant is, zal deze een zeer laag gewicht hebben.

Welnu, genormaliseerd gewicht is een soort weging die wordt gebruikt om het gewogen gemiddelde te krijgen zonder enige deling te hoeven doen.

Het genormaliseerde gewicht is het gewicht van een gegevensitem gedeeld door de som van alle gewichten.

$w_i'=\cfrac{w_i}{\sum_{k=1}^N w_k}$

De som van alle genormaliseerde gewichten is daarom gelijk aan één:

$\sum_{i=1}^N w_i'=1$

Om het gewogen gemiddelde met de genormaliseerde gewichten te berekenen , vermenigvuldigt u eenvoudigweg elk gegevensitem met het genormaliseerde gewicht:

$\displaystyle\overline{x_p}=\sum_{i=1}^N x_i\cdot w_i'=x_1\cdot w_1'+x_2\cdot w_2'+\dots+x_N\cdot w_N'$

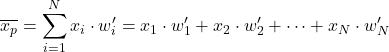
We hebben bijvoorbeeld een statistische steekproef waarvan de gegevens 24, 35, 17, 41 zijn en hun respectievelijke gewichten 4, 9, 6, 3. Om het gewogen gemiddelde van deze gegevensset te vinden, kunnen we eerst de genormaliseerde gewichten berekenen door te delen elk gewicht door de som van alle gewichten:

$\cfrac{4}{4+9+6+3}=0,18$

$\cfrac{9}{4+9+6+3}=0,41$

$\cfrac{6}{4+9+6+3}=0,27$

$\cfrac{3}{4+9+6+3}=0,14$

En vermenigvuldig nu gewoon elke gegevens met het genormaliseerde gewicht en het resultaat is het gewogen gemiddelde:

$\overline{x_p}=24\cdot 0,18+35\cdot 0,41+17\cdot 0,27+41\cdot 0,14=28,91$

Verschil tussen gewogen gemiddelde en rekenkundig gemiddelde

De berekening van het gewogen gemiddelde en het rekenkundig gemiddelde gebeurt op dezelfde manier, aangezien vergelijkbare bewerkingen moeten worden uitgevoerd. Bij gewogen middeling wordt elk gegevenspunt vermenigvuldigd met zijn gewicht en gedeeld door de som van de gewichten, maar bij rekenkundige middeling worden alle gegevens bij elkaar opgeteld en gedeeld door het totale aantal gegevenspunten.

Het verschil tussen het gewogen gemiddelde en het rekenkundig gemiddelde ligt in het concept ervan, aangezien in het rekenkundig gemiddelde wordt aangenomen dat alle gegevens dezelfde waarde hebben, maar in het gewogen gemiddelde heeft elke gegevens een ander gewicht.

Merk op dat als alle gewichten gelijk zijn, het gewogen gemiddelde gelijk is aan het rekenkundig gemiddelde. Je kunt het wiskundige bewijs hieronder zien:

$\begin{aligned}\overline{x_p}&=\cfrac{x_1\cdot w+x_2\cdot w+x_3\cdot w+\dots+x_N\cdot w}{w+w+w+\dots +w}\\[2ex]&= \cfrac{w\cdot (x_1+x_2+\dots+x_N)}{N\cdot w}=\\[2ex] &= \cfrac{x_1+x_2+\dots+x_N}{N}=\overline{x}\end{aligned}$

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder