Hoe u een gewogen kleinste kwadratenregressie uitvoert in r
Een van de belangrijkste aannames van lineaire regressie is dat de residuen met gelijke variantie worden verdeeld op elk niveau van de voorspellende variabele. Deze aanname staat bekend als homoscedasticiteit .
Wanneer deze aanname niet wordt gerespecteerd, wordt er gezegd dat er heteroskedasticiteit aanwezig is in de residuen. Wanneer dit gebeurt, worden de regressieresultaten onbetrouwbaar.
Eén manier om dit probleem op te lossen is het gebruik van gewogen kleinste kwadratenregressie , waarbij gewichten aan waarnemingen worden toegekend, zodat observaties met een lage foutvariantie meer gewicht krijgen omdat ze meer informatie bevatten in vergelijking met waarnemingen met een grotere foutvariantie.
Deze zelfstudie biedt een stapsgewijs voorbeeld van hoe u gewogen kleinste kwadratenregressie kunt uitvoeren in R.
Stap 1: Creëer de gegevens
Met de volgende code wordt een dataframe gemaakt met daarin het aantal gestudeerde uren en de bijbehorende examenscore voor 16 studenten:
df <- data.frame(hours=c(1, 1, 2, 2, 2, 3, 4, 4, 4, 5, 5, 5, 6, 6, 7, 8),
score=c(48, 78, 72, 70, 66, 92, 93, 75, 75, 80, 95, 97, 90, 96, 99, 99))
Stap 2: Voer lineaire regressie uit
Vervolgens gebruiken we de functie lm() om een eenvoudig lineair regressiemodel in te passen dat uren als voorspellende variabele en score alsresponsvariabele gebruikt:
#fit simple linear regression model model <- lm(score ~ hours, data = df) #view summary of model summary(model) Call: lm(formula = score ~ hours, data = df) Residuals: Min 1Q Median 3Q Max -17,967 -5,970 -0.719 7,531 15,032 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 60,467 5,128 11,791 1.17e-08 *** hours 5,500 1,127 4,879 0.000244 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 9.224 on 14 degrees of freedom Multiple R-squared: 0.6296, Adjusted R-squared: 0.6032 F-statistic: 23.8 on 1 and 14 DF, p-value: 0.0002438
Stap 3: Test op heteroskedasticiteit
Vervolgens zullen we een plot maken van de residuen en aangepaste waarden om visueel te controleren op heteroskedasticiteit:
#create residual vs. fitted plot plot( fitted (model), resid (model), xlab=' Fitted Values ', ylab=' Residuals ') #add a horizontal line at 0 abline(0,0)
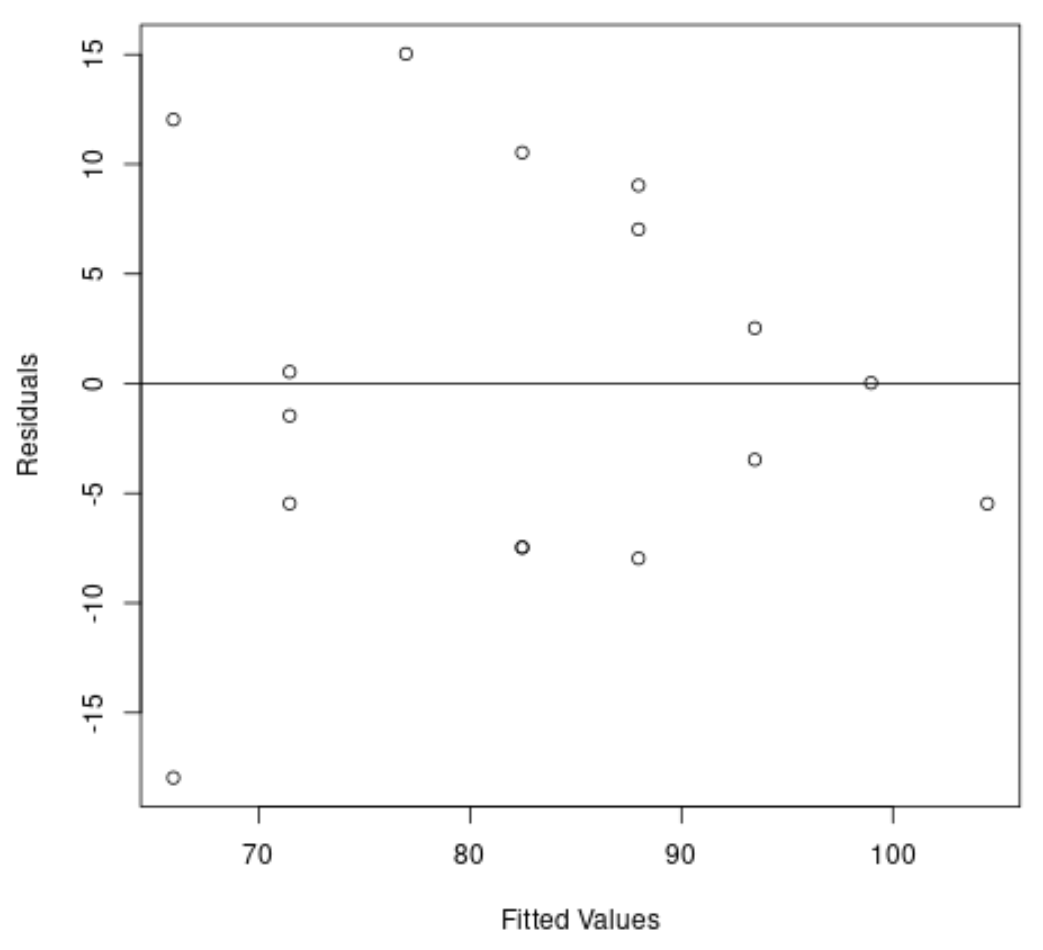
We kunnen uit de grafiek zien dat de residuen een “kegelvorm” hebben: ze zijn niet met gelijke variantie over de grafiek verdeeld.
Om formeel te testen op heteroscedasticiteit, kunnen we een Breusch-Pagan-test uitvoeren:
#load lmtest package library (lmtest) #perform Breusch-Pagan test bptest(model) studentized Breusch-Pagan test data: model BP = 3.9597, df = 1, p-value = 0.0466
De Breusch-Pagan-test gebruikt de volgende nul- en alternatieve hypothesen :
- Nulhypothese (H 0 ): homoscedasticiteit is aanwezig (residuen worden met gelijke variantie verdeeld)
- Alternatieve hypothese ( HA ): heteroscedasticiteit is aanwezig (residuen zijn niet met gelijke variantie verdeeld)
Omdat de p-waarde van de test 0,0466 is, zullen we de nulhypothese verwerpen en concluderen dat heteroscedasticiteit een probleem is in dit model.
Stap 4: Voer een gewogen kleinste kwadratenregressie uit
Omdat heteroscedasticiteit aanwezig is, zullen we gewogen kleinste kwadraten uitvoeren door de gewichten zo in te stellen dat waarnemingen met een lagere variantie meer gewicht krijgen:
#define weights to use
wt <- 1 / lm( abs (model$residuals) ~ model$fitted. values )$fitted. values ^2
#perform weighted least squares regression
wls_model <- lm(score ~ hours, data = df, weights=wt)
#view summary of model
summary(wls_model)
Call:
lm(formula = score ~ hours, data = df, weights = wt)
Weighted Residuals:
Min 1Q Median 3Q Max
-2.0167 -0.9263 -0.2589 0.9873 1.6977
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 63.9689 5.1587 12.400 6.13e-09 ***
hours 4.7091 0.8709 5.407 9.24e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.199 on 14 degrees of freedom
Multiple R-squared: 0.6762, Adjusted R-squared: 0.6531
F-statistic: 29.24 on 1 and 14 DF, p-value: 9.236e-05
Uit de resultaten kunnen we zien dat de schatting van de coëfficiënten voor de urenvoorspellingsvariabele enigszins veranderde en dat de algemene fit van het model verbeterde.
Het gewogen kleinste kwadratenmodel heeft een resterende standaardfout van 1,199 , vergeleken met 9,224 in het oorspronkelijke eenvoudige lineaire regressiemodel.
Dit geeft aan dat de voorspelde waarden geproduceerd door het gewogen kleinste kwadratenmodel veel dichter bij de werkelijke waarnemingen liggen vergeleken met de voorspelde waarden geproduceerd door het eenvoudige lineaire regressiemodel.
Het gewogen kleinste kwadratenmodel heeft ook een R-kwadraat van 0,6762 , vergeleken met 0,6296 in het oorspronkelijke eenvoudige lineaire regressiemodel.
Dit geeft aan dat het gewogen kleinste kwadratenmodel een groter deel van de variantie in examenscores kan verklaren dan het eenvoudige lineaire regressiemodel.
Deze metingen geven aan dat het gewogen kleinste kwadratenmodel beter aansluit bij de gegevens vergeleken met het eenvoudige lineaire regressiemodel.
Aanvullende bronnen
Hoe eenvoudige lineaire regressie uit te voeren in R
Hoe meervoudige lineaire regressie uit te voeren in R
Hoe kwantielregressie uit te voeren in R