Hoe de gini-coëfficiënt in excel te berekenen (met voorbeeld)

De Gini-coëfficiënt , vernoemd naar de Italiaanse statisticus Corrado Gini , is een manier om de inkomensverdeling van een bevolking te meten.

De waarde van de Gini-coëfficiënt varieert van 0 tot 1, waarbij hogere waarden een grotere inkomensongelijkheid vertegenwoordigen en waarbij:

• 0 staat voor perfecte inkomensgelijkheid (iedereen heeft hetzelfde inkomen)
• 1 staat voor perfecte inkomensongelijkheid (één persoon heeft al het inkomen)

Een lijst met Gini-coëfficiënten per land vindt u hier .

Het volgende stapsgewijze voorbeeld laat zien hoe u een Gini-coëfficiënt in Excel kunt berekenen.

Stap 1: Voer de gegevens in

Eerst moeten we waarden invoeren voor twee kolommen: het cumulatieve bevolkingspercentage en het cumulatieve inkomenspercentage van individuen in een bepaald land:

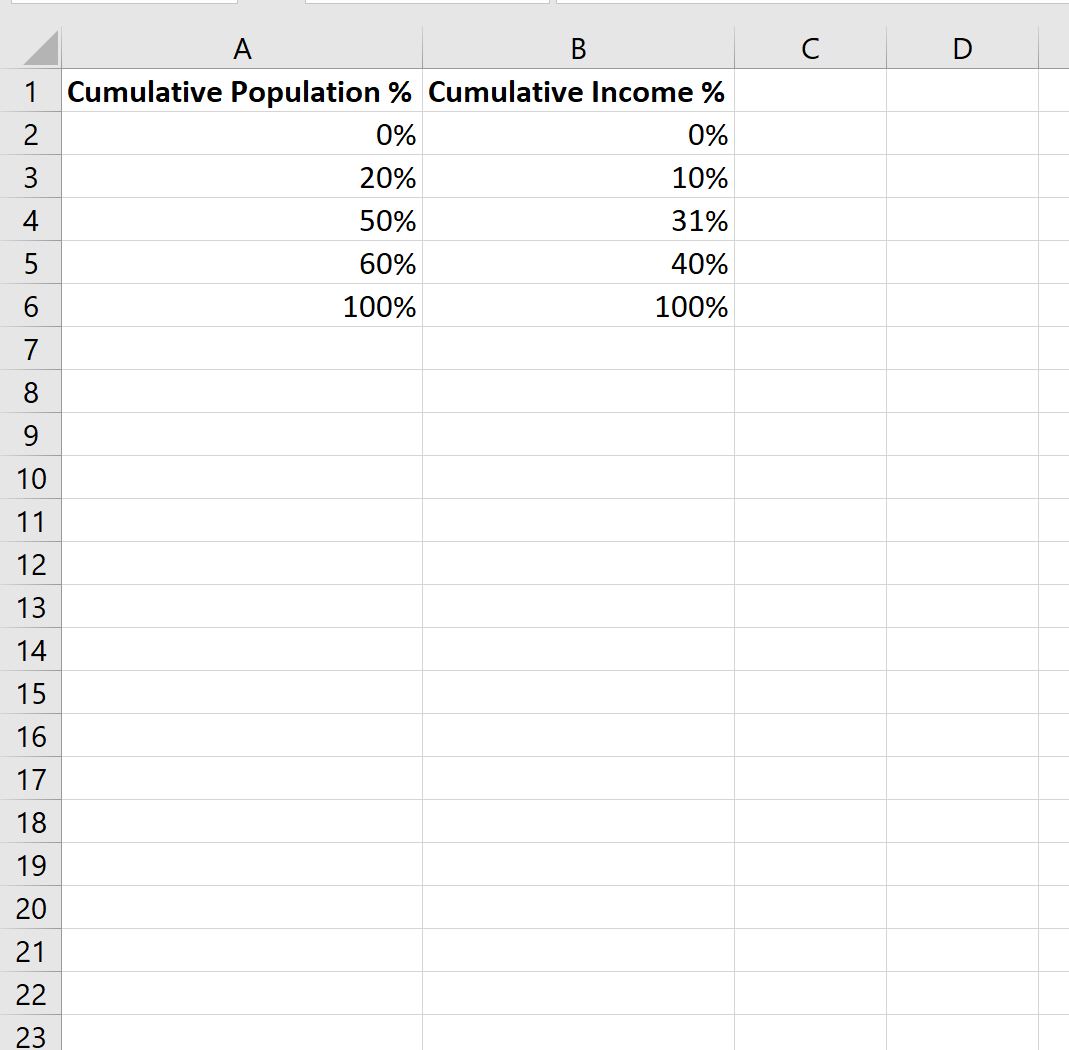
Zo interpreteert u de waarden:

• De armste 20% van de bevolking in dit land vertegenwoordigt 10% van het totale inkomen.
• De armste 50% van de individuen in dit land vertegenwoordigen 31% van het totale inkomen.
• De armste 60% van de mensen in dit land vertegenwoordigen 40% van het totale inkomen.
• 100% van de individuen in dit land zijn verantwoordelijk voor 100% van het totale inkomen.

Stap 2: Bereken de gebieden onder de Lorenz-curve

Vervolgens moeten we de individuele gebieden onder de Lorenz-curve berekenen, een curve die we gebruiken om de inkomensverdeling in een land te visualiseren.

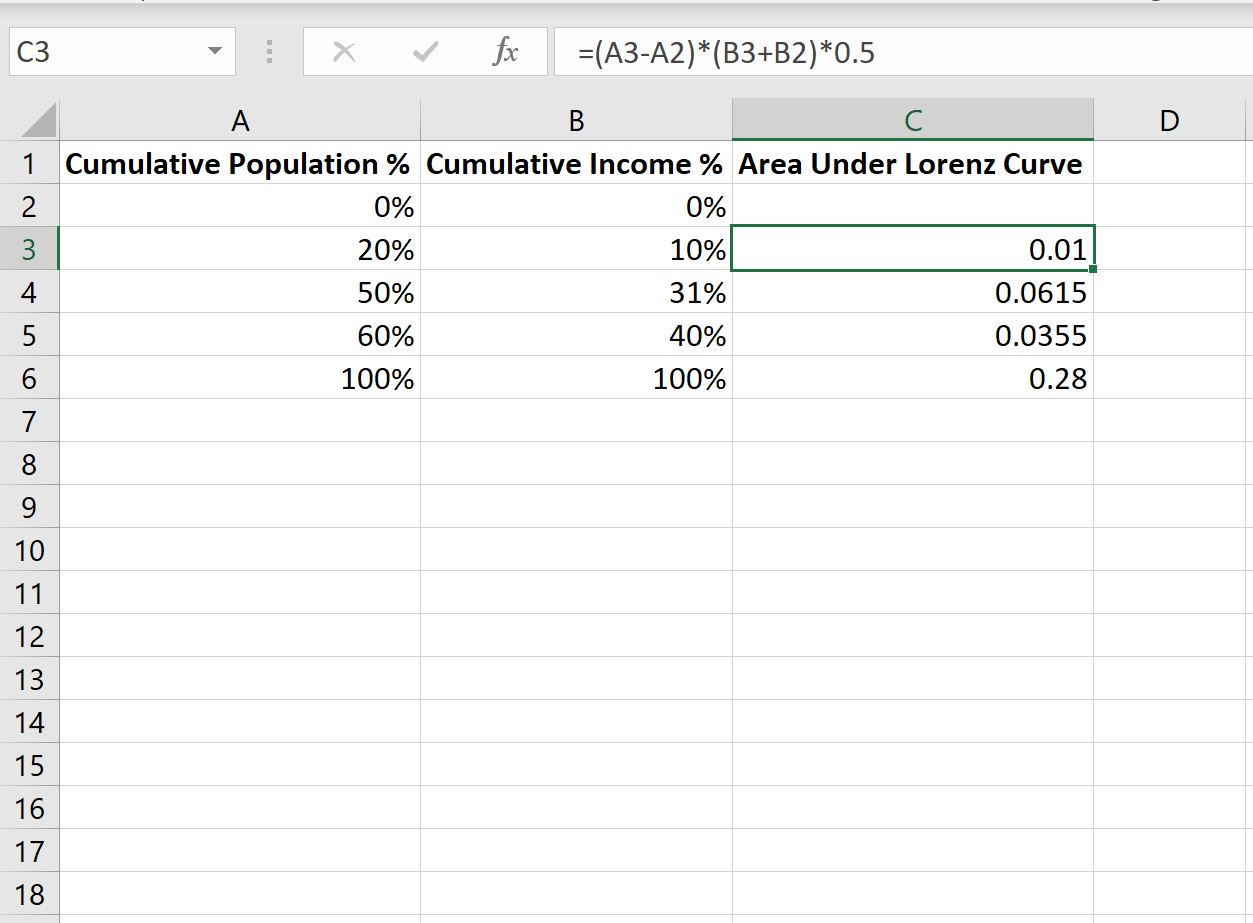
In ons voorbeeld typen we de volgende formule in cel C3 :

 =( A3 - A2 )*( B3 + B2 )*0.5

Vervolgens kopiëren en plakken we deze formule in elke resterende cel in kolom C:

Stap 3: Bereken de Gini-coëfficiënt

Ten slotte kunnen we de volgende formule in cel D2 typen om de Gini-coëfficiënt voor deze populatie te berekenen:

 =1-2*SUM( C3:C6 )

De volgende schermafbeelding laat zien hoe u deze formule in de praktijk kunt gebruiken:

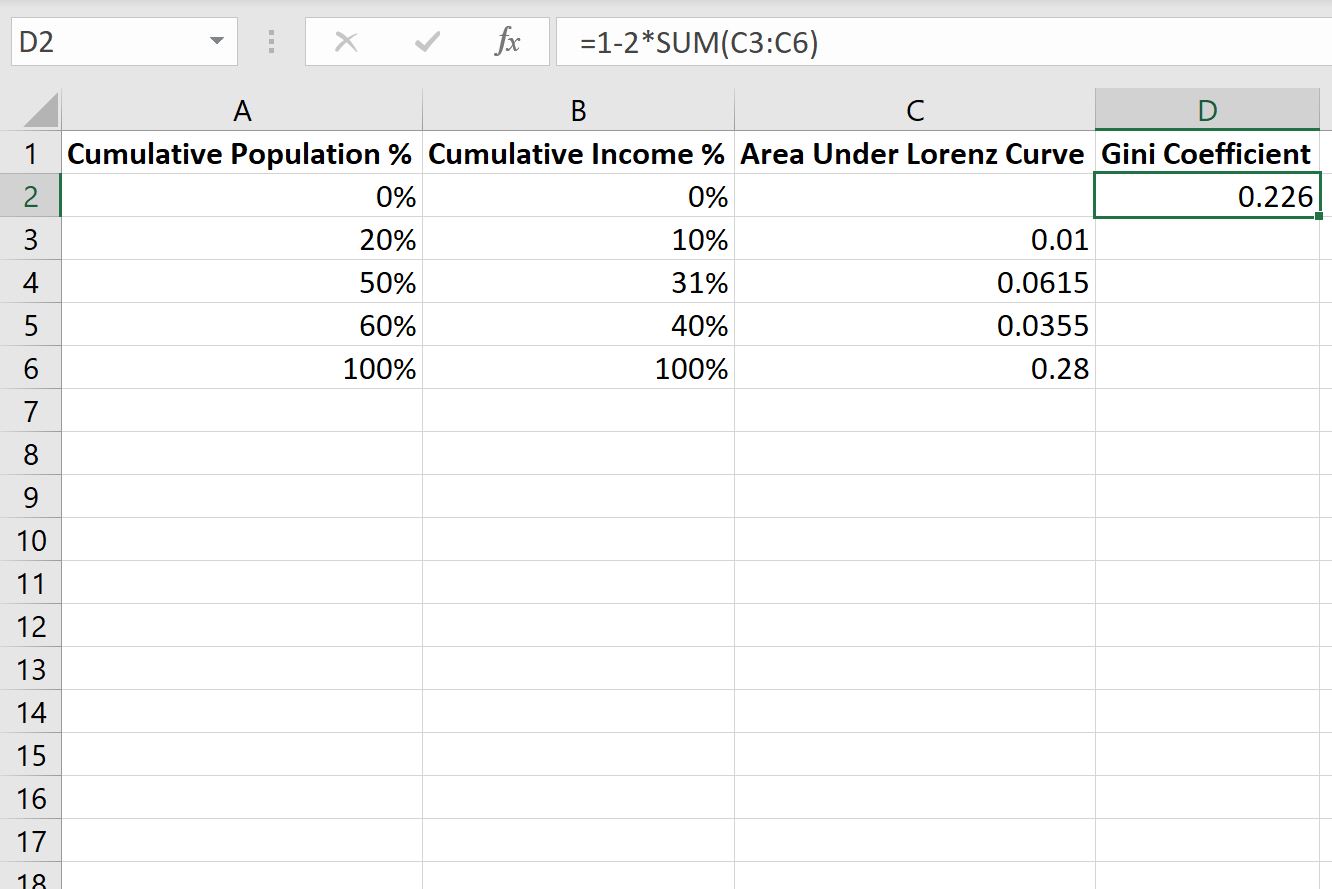
De Gini-coëfficiënt voor deze populatie blijkt 0,226 te zijn.

Dit is een uiterst eenvoudig voorbeeld van hoe u een Gini-coëfficiënt kunt berekenen, maar u kunt exact dezelfde formules gebruiken om een Gini-coëfficiënt te berekenen voor een veel grotere gegevensset.