Wat wordt beschouwd als een goed of slecht restperceel?

Bij regressieanalyse is een residuenplot een soort plot dat de aangepaste waarden van een regressiemodel op de x-as en de residuen van het model langs de y-as weergeeft.

Bij het visueel inspecteren van een restindeling kijken we doorgaans naar twee zaken om te bepalen of de indeling ‘goed’ of ‘slecht’ is:

1. Vertonen de residuen een duidelijke trend?

• In een ‘goede’ restplot vertonen de reststoffen geen duidelijke trend.
• In een ‘slechte’ restgrafiek hebben de residuen een soort patroon, zoals een curve of golf. Dit geeft aan dat het regressiemodel dat we hebben gebruikt niet goed aansluit bij de gegevens.

2. Nemen de residuen systematisch toe of af in variantie?

• In een ‘goed’ residuplot zijn de residuen willekeurig rond nul verspreid, zonder een systematische toename of afname van de variantie.
• In een ‘slecht’ residuplot neemt de variantie van de residuen systematisch toe of af.

Als een residuele plot als „goed“ wordt beoordeeld, betekent dit dat we de resultaten van het regressiemodel kunnen vertrouwen en dat het veilig is om de modelcoëfficiënten te interpreteren.

Als een residuele plot echter als ’slecht‘ wordt beoordeeld, betekent dit dat de modelresultaten onbetrouwbaar zijn en dat we een ander regressiemodel aan de gegevens moeten aanpassen.

De volgende voorbeelden leggen uit hoe u ‘goede’ en ‘slechte’ restplots in de praktijk kunt interpreteren.

Voorbeeld 1: een “goed” restspoor

Stel dat we een regressiemodel passen en de volgende residuele grafiek verkrijgen:

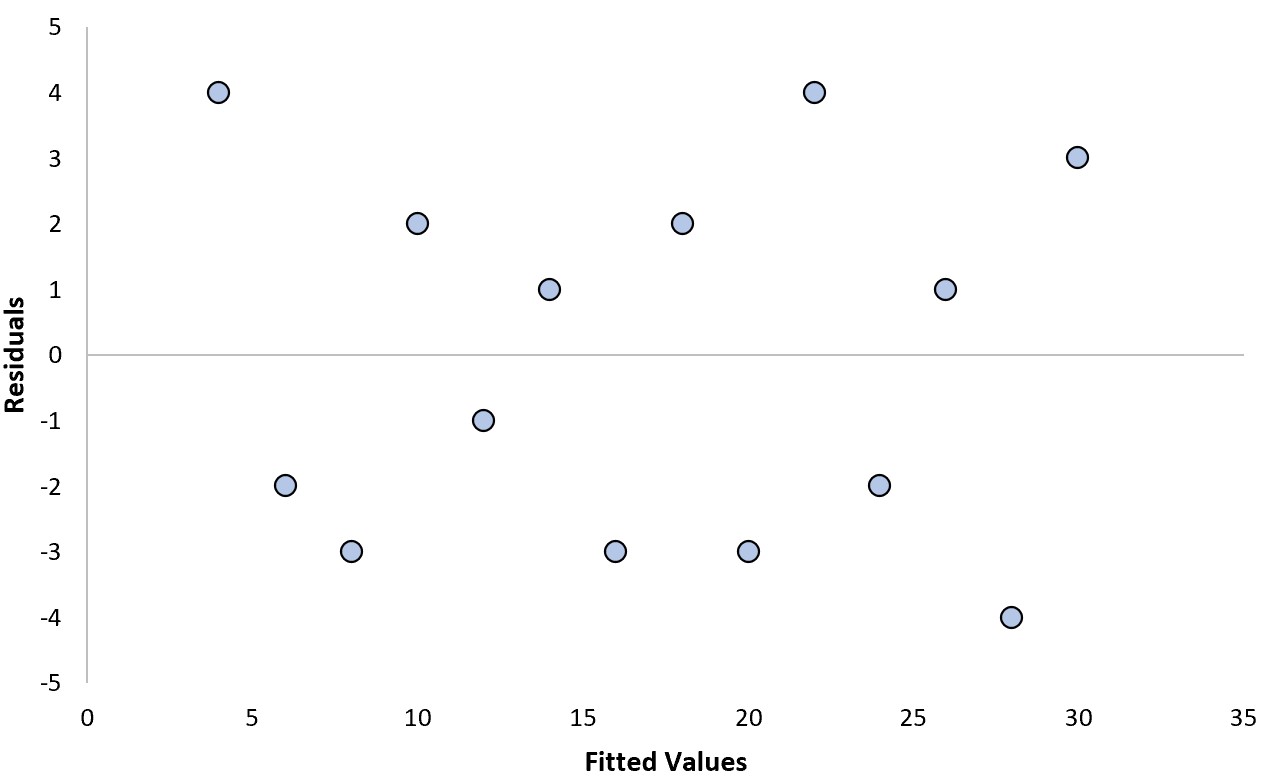
Om te bepalen of dit een ‘goed’ restplot is, kunnen we de volgende twee vragen beantwoorden:

1. Vertonen de residuen een duidelijke trend?

Nee. De residuen zijn willekeurig verspreid rond nul, zonder duidelijk patroon.

2. Nemen de residuen systematisch toe of af in variantie?

Nee. De residuen hebben een vrij constante variantie (dwz de afstand tussen de residuen en de nulwaarde) op elk niveau van de aangepaste waarden.

Omdat we op beide vragen ‘Nee’ hebben geantwoord, beschouwen we dit als een ‘goed’ restplot.

Daarom kunnen we vertrouwen op de resultaten van het regressiemodel en de modelcoëfficiënten veilig interpreteren.

Voorbeeld 2: een “slechte” restplot met een duidelijk model

Stel dat we een regressiemodel passen en de volgende residuele grafiek verkrijgen:

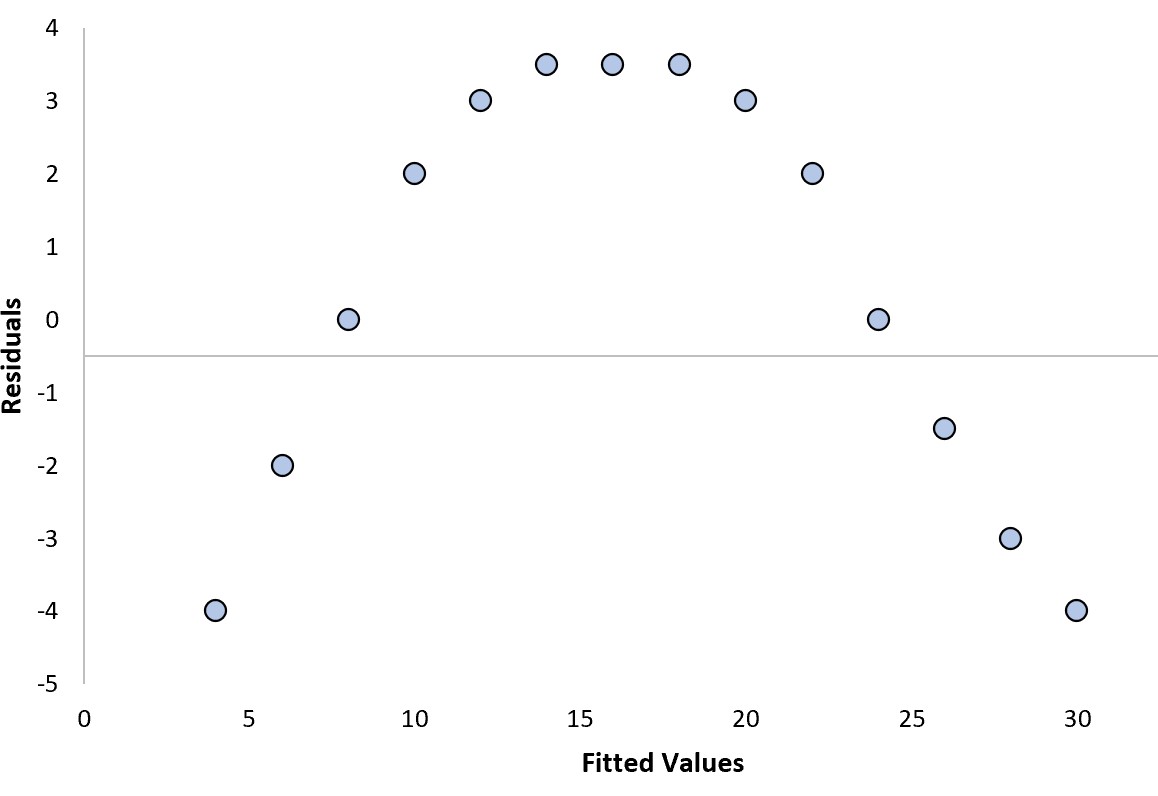
Om te bepalen of dit een ‘goed’ restplot is, kunnen we de volgende twee vragen beantwoorden:

1. Vertonen de residuen een duidelijke trend?

Ja . De residuen vertonen een gebogen patroon.

2. Nemen de residuen systematisch toe of af in variantie?

Ja . De residuen hebben verschillende variantieniveaus op verschillende niveaus van de aangepaste waarden.

Omdat we op ten minste één van deze vragen ‚Ja‘ hebben geantwoord, beschouwen we dit als een ’slecht‘ restplot.

Dit betekent dat het regressiemodel geen goede fit met de gegevens oplevert.

In het bijzonder geeft het gebogen patroon in de grafiek van de residuen aan dat een lineair regressiemodel niet in de gegevens past en dat een kwadratisch regressiemodel waarschijnlijk beter werk zou leveren.

Voorbeeld 3: een “slecht” restdiagram met toenemende variantie

Stel dat we een regressiemodel passen en de volgende residuele grafiek verkrijgen:

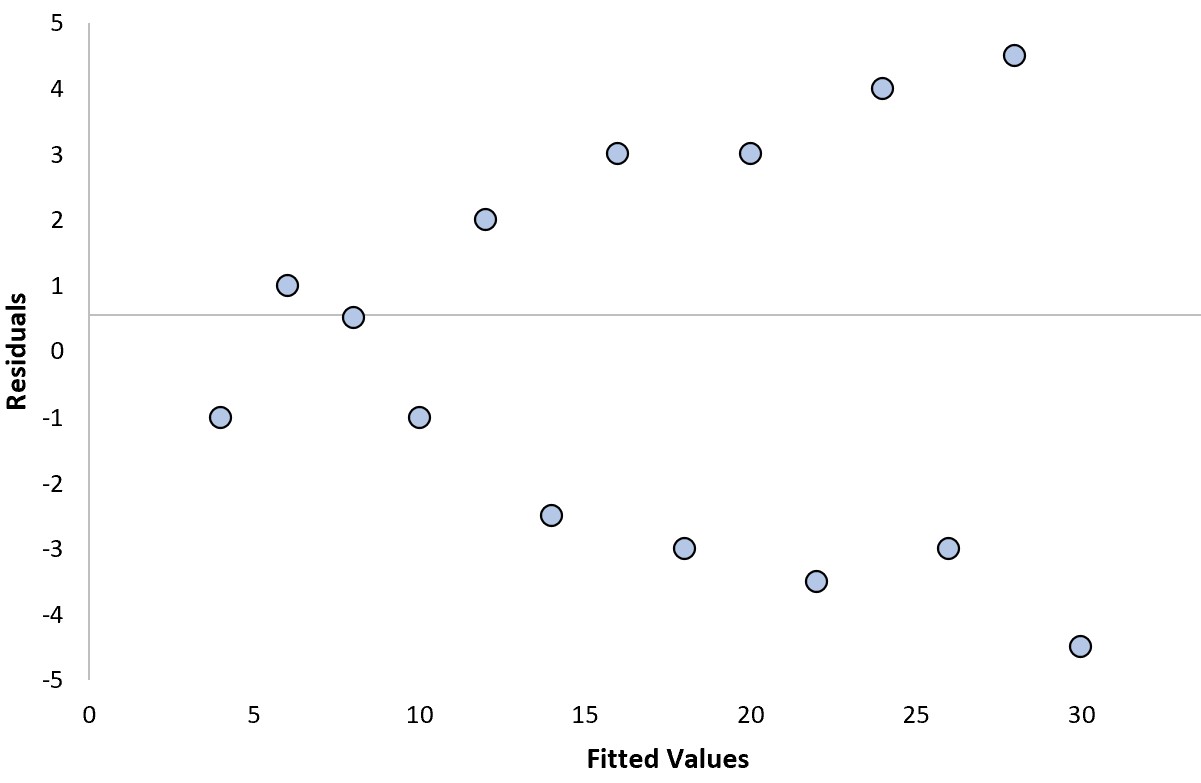
Om te bepalen of dit een ‘goed’ restplot is, kunnen we de volgende twee vragen beantwoorden:

1. Vertonen de residuen een duidelijke trend?

Nee. Er is geen duidelijke trend in de reststoffen te zien.

2. Nemen de residuen systematisch toe of af in variantie?

Ja . De variantie van de residuen neemt toe naarmate de gefitte waarden toenemen.

Omdat we op ten minste één van deze vragen ‚Ja‘ hebben geantwoord, beschouwen we dit als een ’slecht‘ restplot.

In dit specifieke voorbeeld lijden de residuen aan heteroscedasticiteit , wat verwijst naar ongelijke variantie van de residuen op verschillende niveaus van de aangepaste waarden.

Dit betekent dat de resultaten van het regressiemodel mogelijk niet betrouwbaar zijn.

Raadpleeg dit artikel om verschillende manieren te leren om het probleem van heteroskedasticiteit in een regressiemodel op te lossen.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u restplots kunt maken met behulp van verschillende statistische software:

Hoe maak je een restplot in R
Hoe u een restplot maakt in Python
Hoe u een restplot in Excel maakt
Hoe u een restplot maakt in SAS