Hoe u t-tests uitvoert in google spreadsheets

Over het algemeen zijn er drie soorten t-toetsen:

• Een voorbeeld-t-test
• T-test met twee monsters
• Gepaarde monsters t-test

Deze tutorial biedt voorbeelden van hoe u elk van deze tests in Google Spreadsheets kunt uitvoeren.

Voorbeeld: een t-test met één monster

Definitie: Een one-sample t-test wordt gebruikt om te testen of het gemiddelde van een populatie al dan niet gelijk is aan een bepaalde waarde.

Voorbeeld: Een botanicus wil weten of de gemiddelde hoogte van een bepaalde plantensoort gelijk is aan 45 centimeter. Ze neemt een willekeurig monster van twaalf planten en registreert hun hoogte in centimeters.

De volgende schermafbeelding laat zien hoe u een t-test met één steekproef uitvoert om te bepalen of de werkelijke gemiddelde populatielengte gelijk is aan 15 inch:

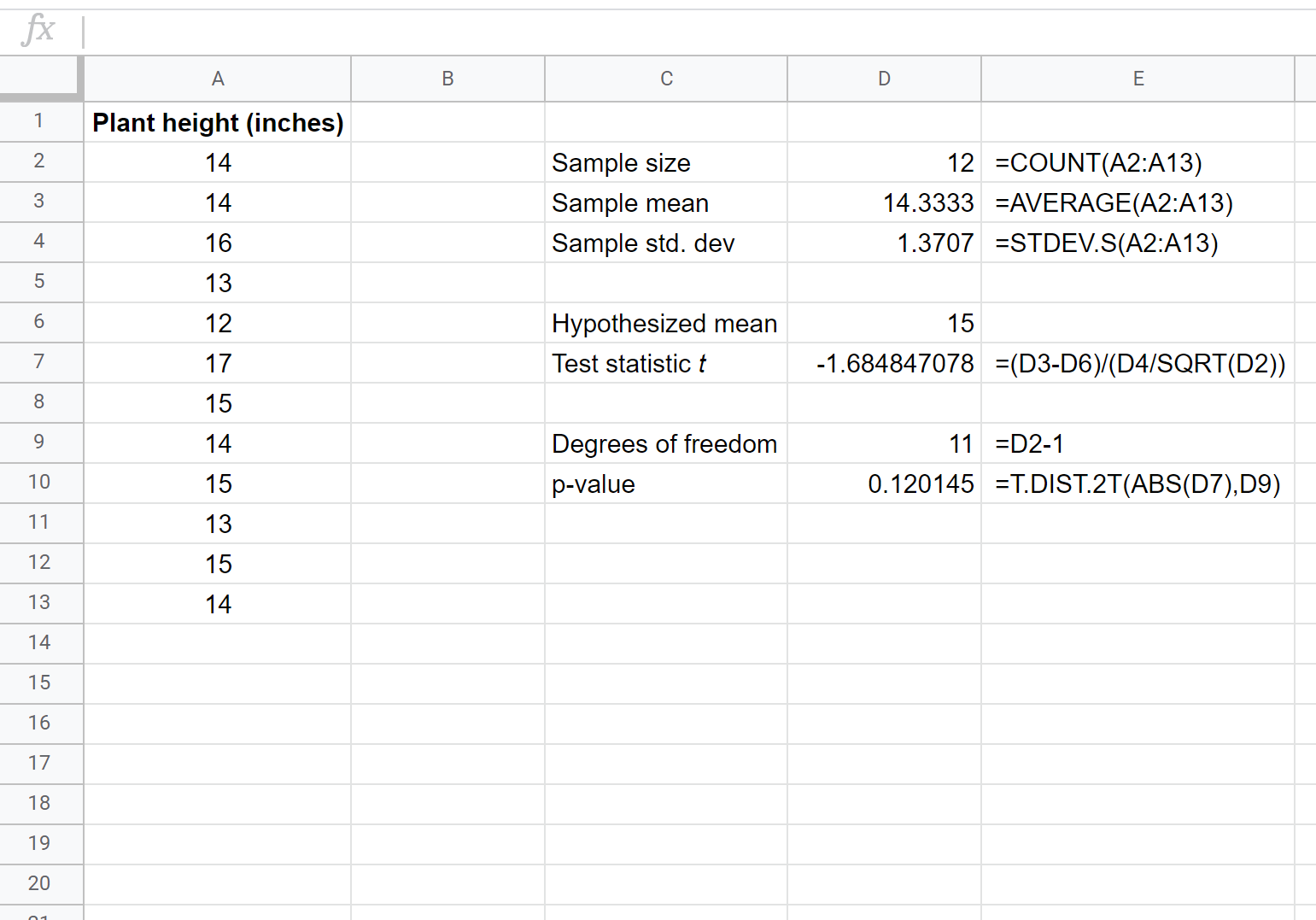
De twee hypothesen voor deze t-test op een bepaald monster zijn als volgt:

H ₀ : µ = 15 (de gemiddelde hoogte van deze plantensoort is 15 inch)

H _A : µ ≠15 (gemiddelde hoogte is niet 15 inch)

Omdat de p-waarde van onze test (0,120145) groter is dan alfa = 0,05, slagen we er niet in de nulhypothese van de test te verwerpen. We hebben niet voldoende bewijs om te zeggen dat de gemiddelde hoogte van deze specifieke plantensoort iets anders is dan 45 centimeter.

Voorbeeld: t-test met twee steekproeven

Definitie: Een t-test met twee steekproeven wordt gebruikt om te testen of de gemiddelden van twee populaties gelijk zijn of niet.

Voorbeeld: Onderzoekers willen weten of twee verschillende plantensoorten in een bepaald land dezelfde gemiddelde hoogte hebben. Ze verzamelen een willekeurig monster van twintig planten van elke soort en registreren de hoogte van elke plant in centimeters.

De volgende schermafbeelding laat zien hoe u een t-test met twee steekproeven uitvoert met behulp van de functie T.TEST() om te bepalen of de gemiddelde lengte van de twee populaties gelijk is:

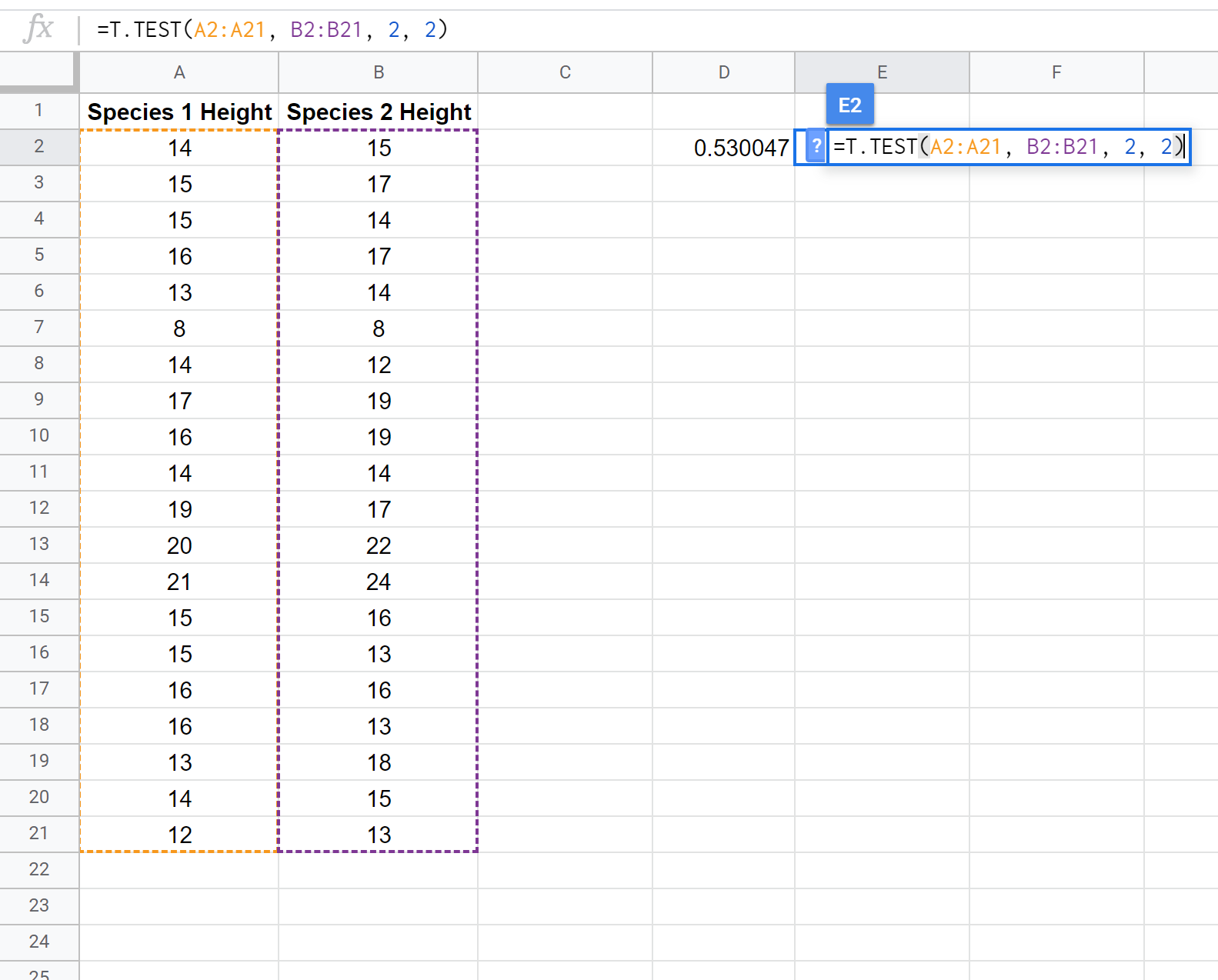
Opmerking: Het is ook mogelijk om een eenzijdige t-toets met twee steekproeven uit te voeren, met of zonder de aanname dat de twee steekproeven dezelfde variantie hebben. Raadpleeg de T.TEST-documentatie om te zien hoe u de testaannames kunt aanpassen.

De twee hypothesen voor deze t-test met twee steekproeven zijn:

H ₀ : μ ₁ = μ ₂ (de twee populatiegemiddelden zijn gelijk)

H ₁ : μ ₁ ≠ μ ₂ (de twee populatiegemiddelden zijn niet gelijk)

Omdat de p-waarde van onze test (0,530047) groter is dan alpha = 0,05, slagen we er niet in de nulhypothese van de test te verwerpen. We hebben niet voldoende bewijs om te zeggen dat de gemiddelde hoogte van deze specifieke plantensoort iets anders is dan 45 centimeter.

Voorbeeld: t-test van gepaarde monsters

Definitie: Een paired samples t-test wordt gebruikt om de gemiddelden van twee monsters te vergelijken wanneer elke waarneming van het ene monster kan worden geassocieerd met een waarneming van het andere monster.

Voorbeeld: We willen weten of een opleiding een significante impact heeft op de prestaties van studenten op een bepaald examen. Om dit te testen, vragen we 20 leerlingen in een klas een voortoets te maken. Vervolgens laten we alle leerlingen twee weken lang deelnemen aan het lesprogramma. Vervolgens maken de leerlingen opnieuw een toets met dezelfde moeilijkheidsgraad.

De volgende schermafbeelding laat zien hoe u een gepaarde steekproef-t-test kunt uitvoeren om het verschil tussen de gemiddelde scores van de eerste en tweede test te vergelijken:

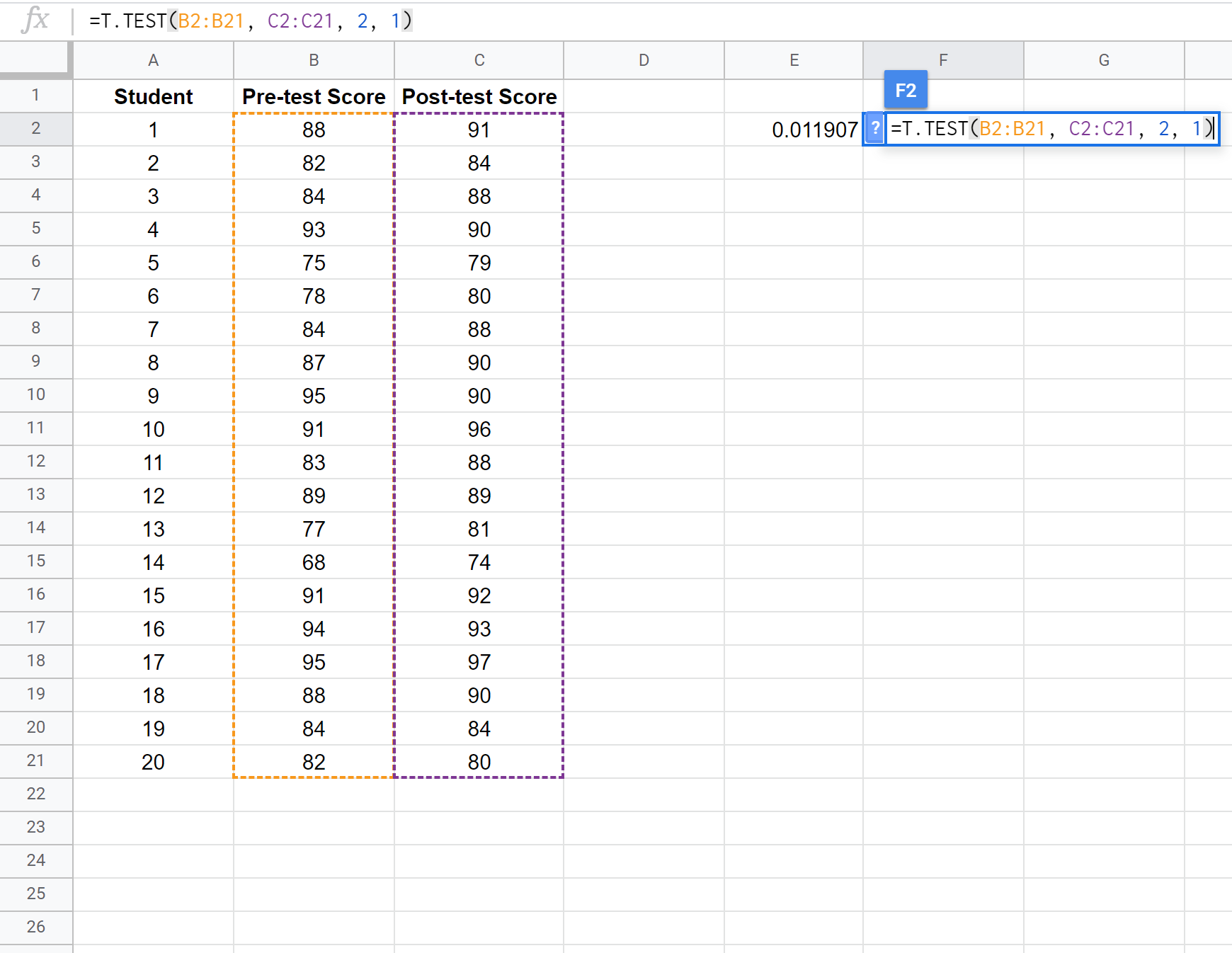
Opmerking: Het is ook mogelijk om een eenzijdige t-toets met twee steekproeven uit te voeren, met of zonder de aanname dat de twee steekproeven dezelfde variantie hebben. Raadpleeg de T.TEST-documentatie om te zien hoe u de testaannames kunt aanpassen.

De twee aannames voor deze t-test met gepaarde monsters zijn:

H ₀ : μ ₁ = μ ₂ (de twee populatiegemiddelden zijn gelijk)

H ₁ : μ ₁ ≠ μ ₂ (de twee populatiegemiddelden zijn niet gelijk)

Omdat de p-waarde van onze test (0,011907) kleiner is dan alpha = 0,05, verwerpen we de nulhypothese van de test. We hebben voldoende bewijs om te zeggen dat er een statistisch significant verschil bestaat tussen de gemiddelde score vóór en na de test.