Hoe de gepoolde variantie in r te berekenen
In de statistieken verwijst clustervariantie naar het gemiddelde van twee of meer clustervarianties.
We gebruiken het woord ‚gepoold‘ om aan te geven dat we twee of meer groepsvarianties ’samenvoegen‘ om één getal te verkrijgen voor de gemeenschappelijke variantie tussen de groepen.
In de praktijk wordt gepoolde variantie het vaakst gebruikt in een t-test met twee steekproeven , die wordt gebruikt om te bepalen of de gemiddelden van twee populaties al dan niet gelijk zijn.
De gepoolde variantie tussen twee monsters wordt doorgaans sp 2 genoemd en wordt als volgt berekend:
s p 2 = ( (n 1 -1)s 1 2 + (n 2 -1)s 2 2 ) / (n 1 +n 2 -2)
Helaas is er geen ingebouwde functie om de gepoolde variantie tussen twee groepen in R te berekenen, maar we kunnen deze vrij eenvoudig berekenen.
Stel dat we bijvoorbeeld de gepoolde variantie tussen de volgende twee groepen willen berekenen:
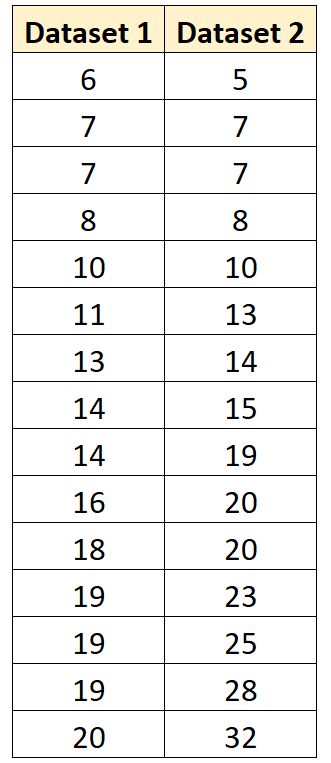
De volgende code laat zien hoe u de gepoolde variantie tussen deze groepen in R kunt berekenen:
#define groups of data x1 <- c(6, 7, 7, 8, 10, 11, 13, 14, 14, 16, 18, 19, 19, 19, 20) x2 <- c(5, 7, 7, 8, 10, 13, 14, 15, 19, 20, 20, 23, 25, 28, 32) #calculate sample size of each group n1 <- length(x1) n2 <- length(x2) #calculate sample variance of each group var1 <- var(x1) var2 <- var(x2) #calculate pooled variance between the two groups pooled <- ((n1-1)*var1 + (n2-1)*var2) / (n1+n2-2) #display pooled variance pooled [1] 46.97143
De gepoolde variantie tussen deze twee groepen blijkt 46,97143 te zijn.
Aanvullende bronnen
Wat is geclusterde variantie? (Definitie en voorbeeld)
Gebundelde kloofcalculator
Hoe u de gepoolde variantie in Excel kunt berekenen
Über den Autor
Dr.benjamin anderson
Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder