Een chi-kwadraattest met de hand uitvoeren (stap voor stap)

Een chikwadraat-goodness-of-fit-test wordt gebruikt om te bepalen of eencategorische variabele al dan niet een hypothetische verdeling volgt.

Het volgende stapsgewijze voorbeeld laat zien hoe u handmatig een chikwadraat-goodness-of-fit-test kunt uitvoeren.

Chi-kwadraat goodness-of-fit-test met de hand

Stel dat we geloven dat een bepaalde dobbelsteen juist is. Met andere woorden, wij geloven dat de dobbelstenen dezelfde kans hebben om bij een bepaalde worp op een 1, een 2, een 3, een 4, een 5 of een 6 terecht te komen.

Om dit te testen, gooien we het 60 keer en noteren we op welk nummer het elke keer terechtkomt. De resultaten zijn als volgt:

• 1 :8 keer
• 2 : 12 keer
• 3 : 18 keer
• 4 :9 keer
• 5 :7 keer
• 6 : 6 keer

Volg de volgende stappen om een chikwadraat-goodness-of-fit-test uit te voeren om te bepalen of de dobbelstenen eerlijk zijn.

Stap 1: Definieer de nul- en alternatieve hypothesen

• H ₀ (nul): de dobbelstenen hebben dezelfde kans om op elk nummer te landen.
• H ₁ (alternatief): De dobbelstenen hebben niet dezelfde kans om op elk nummer te landen.

Stap 2: Bereken de waargenomen en verwachte frequenties

Laten we vervolgens een tabel maken met de waargenomen en verwachte frequenties voor elk getal op de dobbelsteen:

Opmerking : als we denken dat de dobbelsteen eerlijk is, betekent dit dat we verwachten dat hij een gelijk aantal keren op elk getal zal landen – in dit geval elk 10 keer.

Stap 3: Bereken de teststatistiek

De Chi-kwadraattoetsstatistiek, X ² , wordt als volgt berekend:

• X ² = Σ(OE) ² / E

De volgende tabel laat zien hoe u deze teststatistiek berekent:

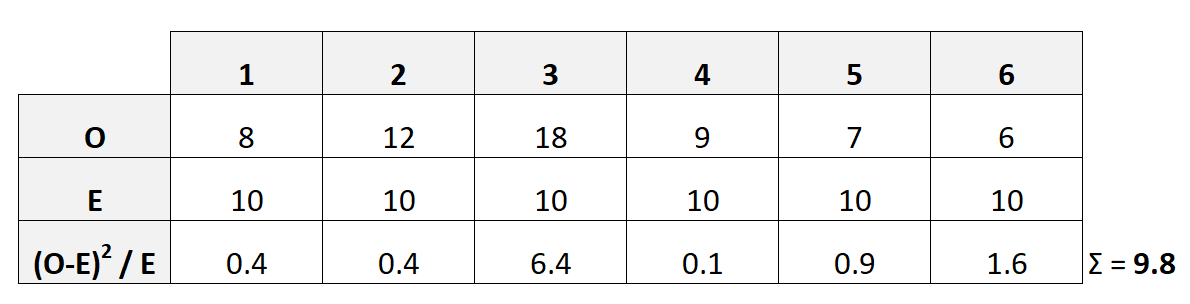
In dit geval blijkt ^X2 9,8 te zijn.

Stap 4: Vind de kritische waarde

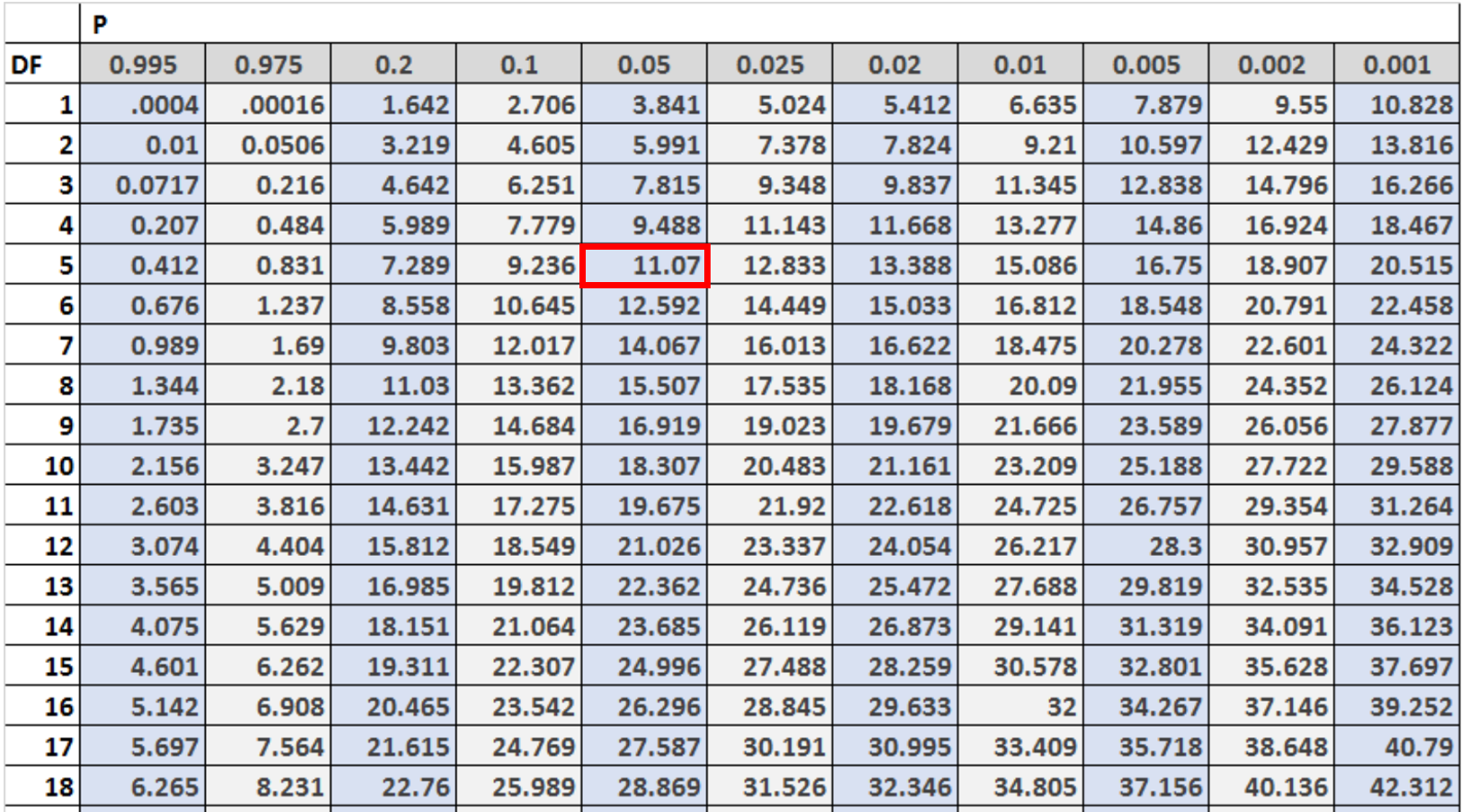
Vervolgens moeten we de kritische waarde vinden in de Chi-kwadraatverdelingstabel die overeenkomt met α = 0,05 en df = (#categories – 1).

In dit geval zijn er 6 categorieën, dus we gebruiken df = 6 – 1 = 5 .

We kunnen zien dat de kritische waarde 11,07 is.

Stap 5: Verwerp de nulhypothese of verwerp deze niet

Omdat onze teststatistiek lager is dan de kritische waarde, slagen we er niet in de nulhypothese te verwerpen. Dit betekent dat we niet genoeg bewijs hebben om te zeggen dat de dobbelstenen oneerlijk zijn.

Aanvullende bronnen

De volgende bronnen bieden aanvullende informatie over de chikwadraat-goodness-of-fit-test:

Inleiding tot de chikwadraat-goodness-of-fit-test
Hoe voer je een chi-kwadraat goodness-of-fit test uit in R
Chi-kwadraat-calculator voor de goodness-of-fit-test