Harmonisch gemiddelde

Hier leggen we uit wat het harmonische gemiddelde is en hoe het wordt berekend (formule). Daarnaast berekenen we stap voor stap het harmonische gemiddelde van een voorbeeld. U zult ook een rekenmachine vinden om het harmonische gemiddelde van elke dataset te bepalen. En ten slotte zul je kunnen zien wat de eigenschappen van het harmonische gemiddelde zijn.

Wat is het harmonische gemiddelde?

Het harmonische gemiddelde is een centrale positiemaatstaf van beschrijvende statistieken. Het harmonische gemiddelde wordt berekend door het totale aantal statistische gegevens te delen door de som van de reciprocals van elke waarde.

Het harmonische gemiddelde wordt gebruikt om gemiddelde snelheden, tijden te berekenen of elektronische berekeningen te maken. Deze functie onderscheidt het harmonische gemiddelde van andere typen gemiddelden, die vaak worden gebruikt bij het berekenen van gemiddelde prijzen of percentages.

De formule voor het harmonische gemiddelde is dus als volgt:

Het harmonische gemiddelde wordt meestal weergegeven met een hoofdletter H.

Andere soorten gemiddelden die bestaan, zijn het rekenkundig gemiddelde, het gewogen gemiddelde, het kwadraatgemiddelde en het geometrische gemiddelde. Het harmonische gemiddelde heeft voor- en nadelen vergeleken met andere soorten gemiddelden, hieronder zullen we zien welke ze zijn.

Hoe het harmonische gemiddelde te berekenen

Om het harmonische gemiddelde te berekenen, moeten de volgende stappen worden uitgevoerd:

1. Bereken het omgekeerde van alle statistische gegevens in de steekproef.
2. Voeg alle berekende inverses toe.
3. Deel het totale aantal gegevens door de som die u in de vorige stap hebt gevonden.
4. Het verkregen resultaat is het harmonische gemiddelde van de statistische steekproef.

👉 Zoals je kunt zien, vereist het bepalen van het harmonische gemiddelde van een dataset veel handelingen, dus het is behoorlijk bewerkelijk om dit met de hand te doen. Om het harmonische gemiddelde te berekenen, raden we daarom aan de onderstaande rekenmachine te gebruiken.

Voorbeeld van harmonisch gemiddelde

Nadat we de theorie over het harmonische gemiddelde hebben gezien, zullen we zien hoe we het harmonische gemiddelde van een reeks gegevens kunnen vinden door een stapsgewijs voorbeeld van de prijs van een aandeel op te lossen.

• Een persoon koopt elk jaar gedurende 5 opeenvolgende jaren aandelen van een bedrijf. Gedurende deze periode fluctueerde de prijs van de aandelen sterk: in het eerste jaar was elk aandeel €7 waard, in het tweede jaar €10, in het derde jaar €15, in het vierde jaar leed de onderneming aanzienlijke financiële verliezen en de de prijs daalde tot € 6 per aandeel en uiteindelijk, in het vijfde jaar, deed het bedrijf een grote investering waardoor de prijs steeg tot € 11. Wat was de gemiddelde aankoopprijs van de aandelen?

Eén optie zou zijn om het rekenkundig gemiddelde te berekenen, dat wil zeggen alle prijzen bij elkaar op te tellen en door vijf te delen. Omdat de aankopen echter in verschillende jaren zijn gedaan, zou het nemen van het rekenkundig gemiddelde een vergissing zijn. We moeten daarom het harmonische gemiddelde van alle prijzen vinden.

Vervolgens passen we de harmonische gemiddelde formule toe:

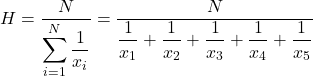
En dan vervangen we de problematische prijswaarden in de formule en berekenen we het harmonische gemiddelde:

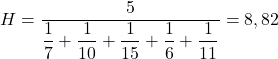
Je moet vijf in de teller van de breuk zetten, omdat er vijf verschillende stukjes informatie zijn.

De gemiddelde prijs van de aandelen die u in deze periode heeft gekocht, bedraagt dus 8,82 euro per aandeel.

Harmonische gemiddelde rekenmachine

Met de volgende rekenmachine kunt u het harmonische gemiddelde van elke statistische gegevensset berekenen.

U moet getallen invoeren met de punt als decimaal scheidingsteken en de getallen scheiden met een spatie. Onthoud dat om het harmonische gemiddelde te vinden, geen enkele waarde nul kan zijn.

Eigenschappen van harmonisch gemiddelde

Het harmonische gemiddelde heeft de volgende kenmerken:

• Grote waarden hebben weinig effect op het harmonische gemiddelde van een ensemble, dat wil zeggen dat een zeer grote waarde ten opzichte van andere gegevens geen merkbare verandering in het harmonische gemiddelde zal veroorzaken.

• Aan de andere kant heeft een kleine waarde een grote invloed op het harmonische gemiddelde van een ensemble, waardoor de waarde ervan aanzienlijk wordt verminderd. De reciproque getallen van de noemer van de formule nemen dan inderdaad zeer grote waarden aan.

• Het harmonische gemiddelde kan niet worden berekend als een van de gegevens nul is, omdat dit onbepaaldheid in de formule zou veroorzaken. In een dergelijk geval wordt gezegd dat het harmonische gemiddelde ongedefinieerd is.

• Het omgekeerde van het harmonische gemiddelde is equivalent aan het rekenkundig gemiddelde van het omgekeerde van de waarnemingen.

• Voor dezelfde groep gegevens zal het harmonische gemiddelde kleiner zijn dan of gelijk zijn aan het rekenkundig gemiddelde.

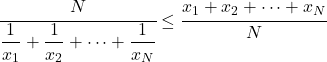
Bereken het harmonische gemiddelde met Excel

Zoals we hebben gezien, kan het handmatig berekenen van het harmonische gemiddelde behoorlijk vervelend zijn, omdat er veel berekeningen moeten worden uitgevoerd. En het wordt nog ingewikkelder als u over een grote hoeveelheid gegevens beschikt. Om het harmonische gemiddelde te vinden, raden we daarom aan een rekenmachine of het Excel-programma te gebruiken.

Het harmonische gemiddelde in Excel wordt berekend met de formule MEAN.ARMO . Dat wil zeggen, om het harmonische gemiddelde van een reeks gegevens te berekenen, moet u deze naar een Excel-werkblad kopiëren en alle gegevens in de functie MEAN.ARMO invoeren.

Om bijvoorbeeld het harmonische gemiddelde te krijgen van de oefening die we hierboven hebben opgelost, schrijft u in een Excel-cel =MEDIA.ARMO(7;10;15;6;11) .

Houd er rekening mee dat als een van de waarden nul is, de functie een fout zal retourneren, omdat het harmonische gemiddelde van een reeks statistische waarden niet kan worden bepaald als een van deze nul is.