Hoe u hefboomstatistieken kunt berekenen in r

In de statistiek wordt een waarneming als een uitbijter beschouwd als de waarde ervan voor de responsvariabele veel groter is dan de rest van de waarnemingen in de dataset.

Op dezelfde manier wordt een waarneming als een hoge hefboomwerking beschouwd als deze een of meer waarden heeft voor de voorspellende variabelen die veel extremer zijn in vergelijking met de rest van de waarnemingen in de dataset.

Een van de eerste stappen bij elk type analyse is het nader bekijken van waarnemingen die een grote invloed hebben, aangezien deze een grote impact kunnen hebben op de resultaten van een bepaald model.

Deze tutorial toont een stapsgewijs voorbeeld van hoe u de hefboomwerking voor elke waarneming in een model in R kunt berekenen en visualiseren.

Stap 1: Maak een regressiemodel

Eerst zullen we een meervoudig lineair regressiemodel maken met behulp van de mtcars- dataset die in R is ingebouwd:

 #load the dataset
data(mtcars)

#fit a regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

Stap 2: Bereken de hefboomwerking voor elke waarneming

Vervolgens zullen we de functie hatvalues() gebruiken om de hefboomwerking voor elke observatie in het model te berekenen:

 #calculate leverage for each observation in the model
hats <- as . data . frame (hatvalues(model))

#display leverage stats for each observation
hats

                    hatvalues(model)
Mazda RX4 0.04235795
Mazda RX4 Wag 0.04235795
Datsun 710 0.06287776
Hornet 4 Drive 0.07614472
Hornet Sportabout 0.08097817
Valiant 0.05945972
Duster 360 0.09828955
Merc 240D 0.08816960
Merc 230 0.05102253
Merc 280 0.03990060
Merc 280C 0.03990060
Merc 450SE 0.03890159
Merc 450SL 0.03890159
Merc 450SLC 0.03890159
Cadillac Fleetwood 0.19443875
Lincoln Continental 0.16042361
Chrysler Imperial 0.12447530
Fiat 128 0.08346304
Honda Civic 0.09493784
Toyota Corolla 0.08732818
Toyota Corona 0.05697867
Dodge Challenger 0.06954069
AMC Javelin 0.05767659
Camaro Z28 0.10011654
Pontiac Firebird 0.12979822
Fiat X1-9 0.08334018
Porsche 914-2 0.05785170
Lotus Europa 0.08193899
Ford Pantera L 0.13831817
Ferrari Dino 0.12608583
Maserati Bora 0.49663919
Volvo 142E 0.05848459

Meestal kijken we nader naar waarnemingen met een hefboomwaarde groter dan 2.

Een eenvoudige manier om dit te doen is door de waarnemingen te sorteren op basis van hun hefboomwaarde, in aflopende volgorde:

 #sort observations by leverage, descending
hats[ order (-hats[' hatvalues(model) ']), ]

 [1] 0.49663919 0.19443875 0.16042361 0.13831817 0.12979822 0.12608583
 [7] 0.12447530 0.10011654 0.09828955 0.09493784 0.08816960 0.08732818
[13] 0.08346304 0.08334018 0.08193899 0.08097817 0.07614472 0.06954069
[19] 0.06287776 0.05945972 0.05848459 0.05785170 0.05767659 0.05697867
[25] 0.05102253 0.04235795 0.04235795 0.03990060 0.03990060 0.03890159
[31] 0.03890159 0.03890159

We kunnen zien dat de hoogste hefboomwaarde 0,4966 is. Omdat dit getal niet groter is dan 2, weten we dat geen van de waarnemingen in onze dataset een grote invloed heeft.

Stap 3: Visualiseer de hefboomwerking voor elke observatie

Ten slotte kunnen we een snel diagram maken om de hefboomwerking voor elke waarneming te visualiseren:

 #plot leverage values for each observation
plot(hatvalues(model), type = ' h ')

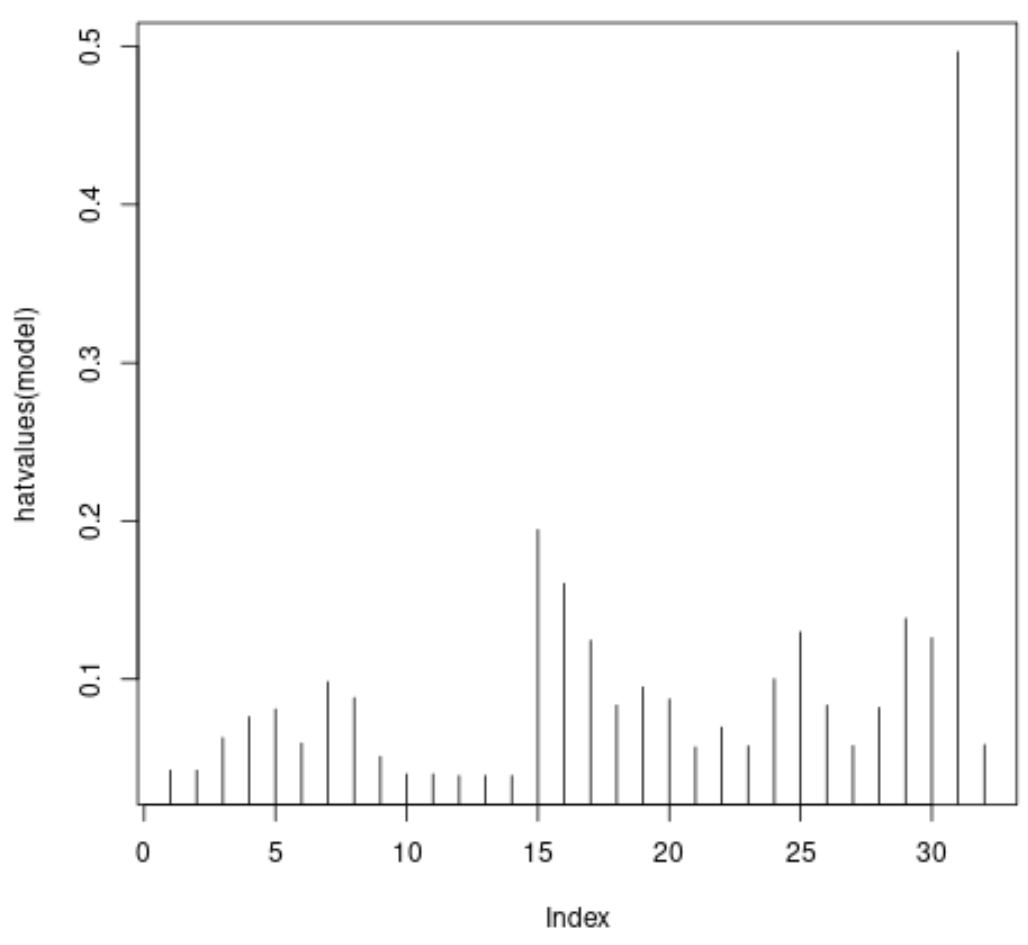
Op de x-as wordt de index van elke waarneming in de dataset weergegeven en op de y-waarde wordt de overeenkomstige hefboomstatistiek voor elke waarneming weergegeven.

Aanvullende bronnen

Hoe eenvoudige lineaire regressie uit te voeren in R
Hoe meervoudige lineaire regressie uit te voeren in R
Hoe maak je een restplot in R