De breusch-pagan-test: definitie en voorbeeld

Een van de belangrijkste aannames van lineaire regressie is dat de residuen met gelijke variantie worden verdeeld op elk niveau van de voorspellende variabele. Deze aanname staat bekend als homoscedasticiteit .

Wanneer deze veronderstelling niet wordt gerespecteerd, wordt er gezegd dat er heteroscedasticiteit aanwezig is in de residuen. Wanneer dit gebeurt, worden de regressieresultaten onbetrouwbaar.

Eén manier om visueel te detecteren of heteroscedasticiteit aanwezig is, is door een grafiek van de residuen te maken tegen de aangepaste waarden uit het regressiemodel.

Als de residuen zich meer verspreiden bij hogere waarden in de grafiek, is dit een veelbetekenend teken van de aanwezigheid van heteroscedasticiteit.

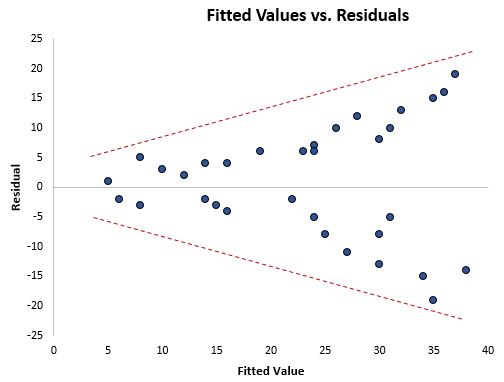
Een formele statistische test die we kunnen gebruiken om te bepalen of heteroscedasticiteit aanwezig is, is de Breusch-Pagan-test .

Deze tutorial geeft een korte uitleg van de Breusch-Pagan-test, samen met een voorbeeld.

Wat is de Breusch-Pagan-test?

De Breusch-Pagan-test wordt gebruikt om te bepalen of heteroskedasticiteit al dan niet aanwezig is in een regressiemodel.

De test maakt gebruik van de volgende nul- en alternatieve hypothesen :

• Nulhypothese (H ₀ ): homoscedasticiteit is aanwezig (residuen worden met gelijke variantie verdeeld)
• Alternatieve hypothese ( _HA ): heteroscedasticiteit is aanwezig (residuen zijn niet met gelijke variantie verdeeld)

Als de p-waarde van de test onder een bepaald significantieniveau ligt (dwz α = 0,05), dan verwerpen we de nulhypothese en concluderen we dat heteroscedasticiteit aanwezig is in het regressiemodel.

We gebruiken de volgende stappen om een Breusch-Pagan-test uit te voeren:

1. Pas het regressiemodel aan.

2. Bereken de kwadraten van de modelresiduen.

3. Pas een nieuw regressiemodel toe, waarbij u de kwadraten van de residuen als responswaarden gebruikt.

4. Bereken de Chi-kwadraat X ^2- teststatistiek in de vorm n*R ² _new , waarbij:

• n: Het totale aantal waarnemingen
• R ² _nieuw : Het R-kwadraat van het nieuwe regressiemodel dat de kwadraten van de residuen als responswaarden gebruikte

Als de p-waarde die overeenkomt met deze chikwadraatteststatistiek met p (het aantal voorspellers) vrijheidsgraden onder een bepaald significantieniveau ligt (dwz α = 0,05), verwerp dan de nulhypothese en concludeer dat heteroskedasticiteit aanwezig is .

Anders verwerp je de nulhypothese niet. In dit geval wordt aangenomen dat er sprake is van homoscedasticiteit.

Houd er rekening mee dat de meeste statistische software de Breusch-Pagan-test gemakkelijk kan uitvoeren, dus u zult deze stappen waarschijnlijk nooit met de hand hoeven uit te voeren, maar het is handig om te weten wat er achter de schermen gebeurt.

Een voorbeeld van de Breusch-Pagan-test

Stel dat we de volgende dataset hebben met informatie over 10 verschillende basketbalspelers:

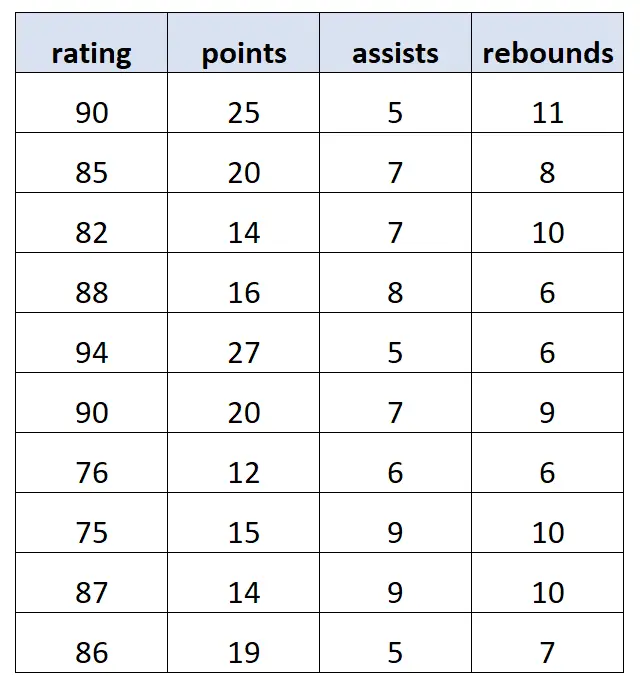
Met behulp van statistische software passen we het volgende meervoudige lineaire regressiemodel toe:

score = 62,47 + 1,12*(punten) + 0,88*(assisten) – 0,43*(rebounds)

Vervolgens gebruiken we dit model om voorspellingen te doen over de beoordeling van elke speler en berekenen we de gekwadrateerde residuen (dwz het kwadraat van het verschil tussen de voorspelde beoordeling en de werkelijke beoordeling):

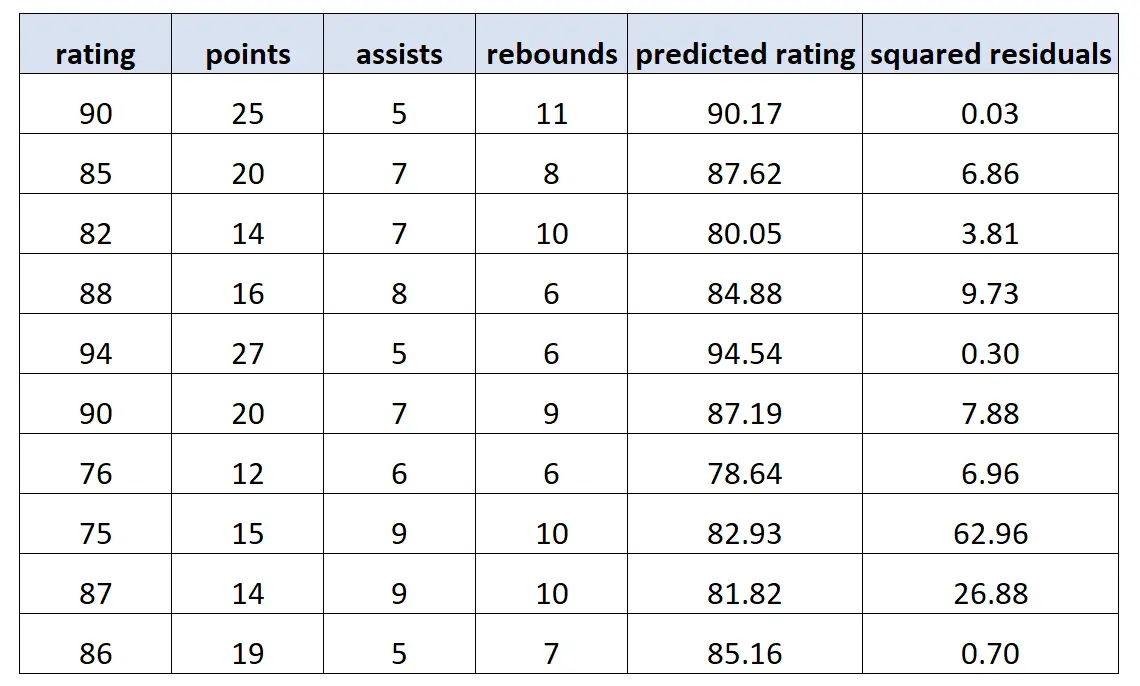
Vervolgens passen we een nieuw regressiemodel aan, waarbij we de kwadraten van de residuen opnieuw als responswaarden gebruiken en de oorspronkelijke voorspellende variabelen opnieuw als voorspellende variabelen. Wij vinden het volgende:

• n: 10
• ^R2 _nieuw : 0,600395

Onze Chi-kwadraattoetsstatistiek voor de Breusch-Pagantoets is dus n*R ² _new = 10*.600395 = 6.00395 . De vrijheidsgraden zijn p = 3 voorspellende variabelen.

Volgens dechikwadraat-naar-P-waardecalculator is de p-waarde die overeenkomt met X ² = 6,00395 met 3 vrijheidsgraden 0,111418 .

Omdat deze p-waarde niet kleiner is dan 0,05, slagen we er niet in de nulhypothese te verwerpen. We nemen daarom aan dat homoscedasticiteit aanwezig is.

De Breusch-Pagan-test in de praktijk

De volgende tutorials bieden stapsgewijze voorbeelden van hoe u de Breusch-Pagan-test in verschillende statistische programma’s kunt uitvoeren:

Hoe u een Breusch-Pagan-test uitvoert in Excel
Hoe voer je een Breusch-Pagan-test uit in R
Hoe een Breusch-Pagan-test uit te voeren in Python
Hoe een Breusch-Pagan-test uit te voeren in Stata