De drie aannames van anova met herhaalde metingen

Een ANOVA met herhaalde metingen wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer groepen waarin in elke groep dezelfde onderwerpen voorkomen.

Voordat we echter een ANOVA met herhaalde metingen uitvoeren, moeten we ervoor zorgen dat aan de volgende aannames wordt voldaan:

1. Onafhankelijkheid: Elke waarneming moet onafhankelijk zijn.

2. Normaliteit: De verdeling van de responsvariabele is normaal verdeeld.

3. Sfericiteit: De varianties van de verschillen tussen alle combinaties van verwante groepen moeten gelijk zijn.

Als een of meer van deze aannames worden geschonden, kunnen de resultaten van ANOVA met herhaalde metingen onbetrouwbaar zijn.

In dit artikel geven we een uitleg voor elke aanname, hoe je kunt bepalen of aan de aanname wordt voldaan en wat je moet doen als er niet aan wordt voldaan.

Hypothese 1: Onafhankelijkheid

Bij herhaalde ANOVA-metingen wordt ervan uitgegaan dat elke waarneming in uw dataset onafhankelijk is van alle andere waarnemingen.

Hoe te bepalen of aan deze veronderstelling wordt voldaan

De eenvoudigste manier om deze aanname te verifiëren is door te verifiëren dat elk individu in de dataset willekeurig uit de populatie is getrokken met behulp van een willekeurige steekproefmethode .

Als een willekeurige steekproefmethode werd gebruikt, kan worden aangenomen dat elke waarneming onafhankelijk is.

Wat te doen als deze veronderstelling niet wordt gerespecteerd

Als niet aan deze veronderstelling wordt voldaan, is er sprake van een ernstig probleem, omdat de waarden van elk individu op de een of andere manier met elkaar verband kunnen houden.

Vaak is de enige oplossing in dit scenario het rekruteren van individuen voor een nieuw onderzoek met behulp van een willekeurige steekproefmethode.

Hypothese 2: normaliteit

Bij herhaalde ANOVA-metingen wordt ervan uitgegaan dat de verdeling van deresponsvariabele normaal verdeeld is.

Hoe te bepalen of aan deze veronderstelling wordt voldaan

Er zijn twee manieren om te controleren of deze hypothese waar is:

1. Maak een histogram of QQ-plot

U kunt visueel controleren of de verdeling van de responsvariabele bij benadering normaal verdeeld is door een histogram of QQ-plot te maken.

Als u een histogram maakt, controleert u eenvoudigweg of de verdeling van de responsvariabele ongeveer de vorm van een „bel“ volgt. Als dat zo is, kun je er vaak van uitgaan dat aan de normaliteitsaanname is voldaan:

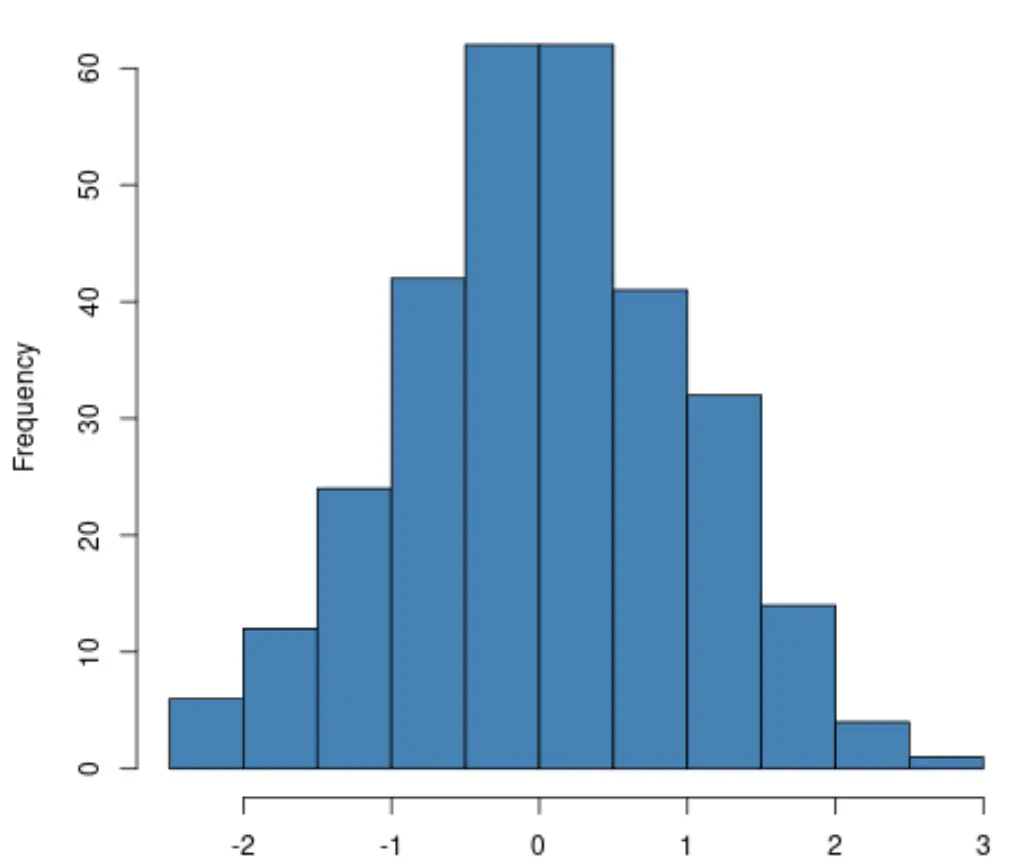
Als u een QQ-plot maakt, controleer dan of de gegevenspunten langs een rechte diagonale lijn liggen. Als dat zo is, kun je er in het algemeen van uitgaan dat aan de normaliteitsaanname is voldaan:

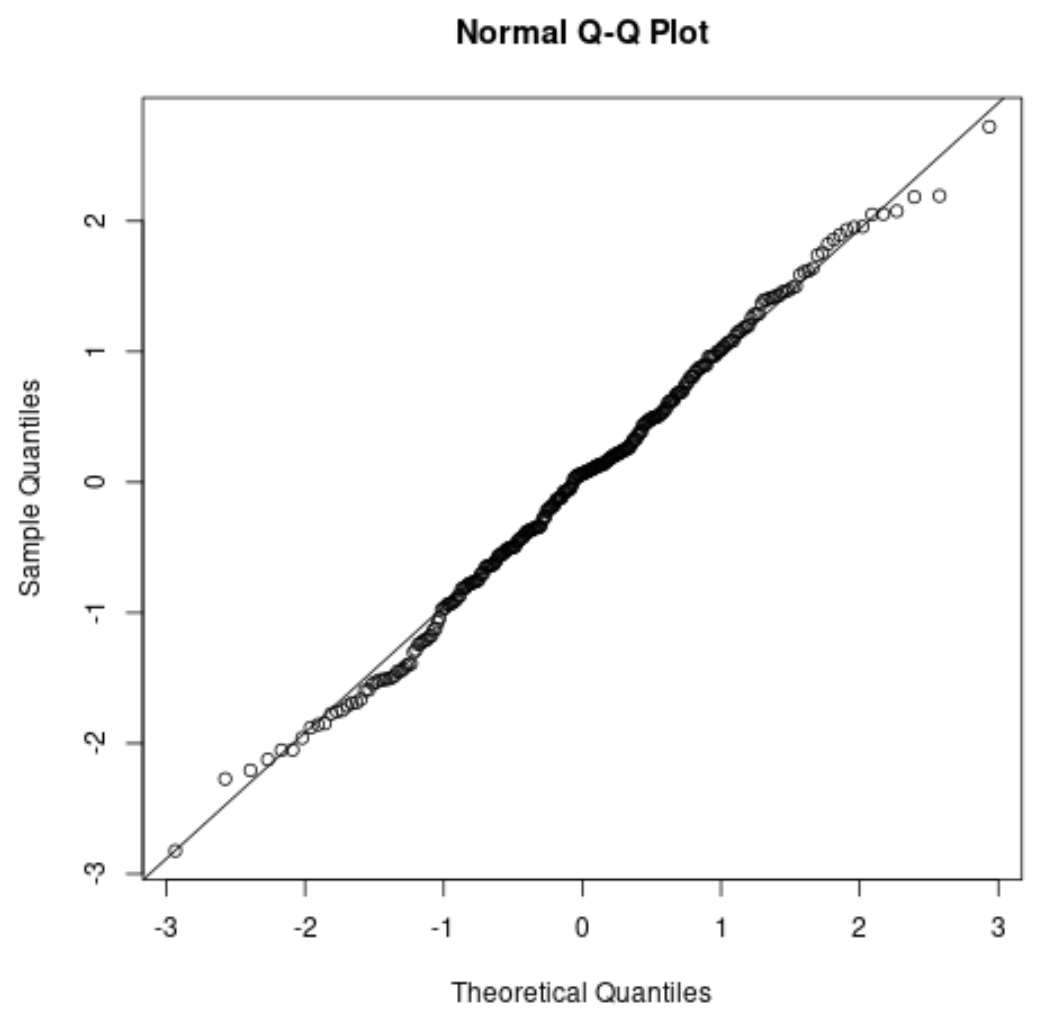
Gerelateerd:QQ-plots gebruiken om de normaliteit te controleren

2. Voer een formele statistische test uit

U kunt ook een Shapiro-Wilk-test uitvoeren om te controleren op normaliteit. Als de p-waarde van de test kleiner is dan 0,05, duidt dit erop dat de gegevens niet normaal verdeeld zijn.

Houd er echter rekening mee dat wanneer u met extreem grote steekproeven werkt, statistische tests zoals de Shapiro-Wilk-test u bijna altijd zullen vertellen dat uw gegevens niet normaal zijn.

Om deze reden is het vaak het beste om uw gegevens visueel te inspecteren met behulp van grafieken zoals histogrammen en QQ-plots. Door alleen maar naar de grafieken te kijken, kun je een redelijk goed idee krijgen of de gegevens normaal verdeeld zijn of niet.

Wat te doen als deze veronderstelling niet wordt gerespecteerd

Over het algemeen wordt een ANOVA met herhaalde metingen als behoorlijk robuust beschouwd tegen schendingen van de normaliteitsaanname, zolang de steekproefomvang groot genoeg is.

Als de normaliteitsaanname ernstig wordt geschonden, heb je twee keuzes:

1. Transformeer de responswaarden van uw gegevens zodat de verdelingen normaler verdeeld zijn.

2. Voer een gelijkwaardige niet-parametrische test uit, zoals de Friedman-test , waarbij geen aanname van normaliteit vereist is.

Veronderstelling 3: Sfericiteit

Een ANOVA met herhaalde metingen gaat uit van sfericiteit , dat wil zeggen dat de varianties van de verschillen tussen alle combinaties van verwante groepen gelijk moeten zijn.

Als niet aan deze aanname wordt voldaan, wordt de F-ratio te hoog en worden de resultaten van herhaalde ANOVA-metingen onbetrouwbaar.

Hoe te bepalen of aan deze veronderstelling wordt voldaan

Om te testen of aan deze veronderstelling wordt voldaan, kunnen we Mauchly’s test van sfericiteit uitvoeren.

Deze test maakt gebruik van de volgende nul- en alternatieve hypothese:

• H ₀ : De varianties van de verschillen zijn gelijk
• H _A : De varianties van de verschillen zijn niet gelijk

Als de p-waarde van de test onder een bepaald significantieniveau ligt (bijvoorbeeld α = 0,05), dan verwerpen we de nulhypothese en concluderen we dat de varianties van de verschillen niet gelijk zijn.

Anders, als de p-waarde niet minder is dan een bepaald significantieniveau (bijvoorbeeld α = 0,05), slagen we er niet in de nulhypothese te verwerpen en concluderen we dat aan de aanname van sfericiteit is voldaan.

Afhankelijk van de statistische software die u gebruikt, zien de resultaten van deze test er als volgt uit:

Omdat de p-waarde niet kleiner is dan 0,05, zullen we er niet in slagen de nulhypothese te verwerpen en te concluderen dat in dit specifieke voorbeeld aan de aanname van sfericiteit is voldaan.

Wat te doen als deze veronderstelling niet wordt gerespecteerd

Als we de nulhypothese van Mauchly’s test van sfericiteit verwerpen, passen we doorgaans een correctie toe op de vrijheidsgraden die worden gebruikt om de F-waarde te berekenen in de ANOVA-tabel met herhaalde metingen.

Er zijn drie oplossingen die we kunnen toepassen:

• Huynh-Feldt (minst conservatief)
• Serre-Geisser
• Ondergrens (meest conservatieve)

Elk van deze correcties heeft de neiging de p-waarden in de ANOVA-uitvoertabel met herhaalde metingen te verhogen om rekening te houden met het feit dat de aanname van sfericiteit wordt geschonden.

Deze p-waarden kunnen we vervolgens gebruiken om te bepalen of we de nulhypothese van ANOVA met herhaalde metingen wel of niet moeten verwerpen.

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over ANOVA met herhaalde metingen:

Een inleiding tot ANOVA met herhaalde metingen
Herhaalde metingen ANOVA-calculator
Hoe de resultaten van een ANOVA met herhaalde metingen te rapporteren
Eenrichtings-ANOVA en herhaalde metingen-ANOVA: het verschil