Heteroskedasticiteit

In dit artikel wordt uitgelegd wat heteroscedasticiteit in de statistiek is. Daarnaast zul je ontdekken wat de oorzaak is van heteroscedasticiteit, wat de gevolgen ervan zijn en hoe je dit kunt oplossen.

Wat is heteroscedasticiteit?

In de statistiek is heteroskedasticiteit een kenmerk dat een regressiepatroon vertoont dat impliceert dat de foutvariantie niet constant is. Met andere woorden: een heteroscedastisch model betekent dat de fouten ervan een onregelmatige variantie hebben. Het model wordt dan heteroskedastisch genoemd.

Houd er rekening mee dat de fout (of residu) wordt gedefinieerd als het verschil tussen de werkelijke waarde en de door het regressiemodel geschatte waarde.

Bij het bouwen van een regressiemodel wordt de fout die door elke waarneming wordt gemaakt, berekend met behulp van de vorige uitdrukking. Een statistisch model is dus heteroscedastisch wanneer de variantie van de berekende fouten niet constant is gedurende de waarnemingen, maar eerder varieert.

Hoewel het heel eenvoudig lijkt, is het belangrijk dat een regressiemodel geen heteroskedasticiteit vertoont, aangezien de berekening van het model gebaseerd is op het feit dat de variantie van de residuen constant is; in feite is het een van de eerdere aannames van de regressiemodellen.

Er zijn bepaalde statistische tests die heteroskedasticiteit kunnen detecteren, zoals de White-test of de Goldfeld-Quandt-test. Meestal kan hun heteroskedasticiteit echter worden geïdentificeerd door de residuen in een grafiek weer te geven.

Oorzaken van heteroscedasticiteit

De meest voorkomende oorzaken van heteroskedasticiteit in een model zijn:

• Wanneer het gegevensbereik erg breed is in vergelijking met het gemiddelde. Als er in dezelfde statistische steekproef zeer grote waarden en zeer kleine waarden voorkomen, is het waarschijnlijk dat het verkregen regressiemodel heteroscedastisch is.
• Het weglaten van variabelen in het regressiemodel resulteert ook in heteroskedasticiteit. Als een relevante variabele niet in het model is opgenomen, zal de variatie ervan logischerwijs in de residuen worden opgenomen, en deze hoeft niet noodzakelijkerwijs vast te liggen.
• Op dezelfde manier kan een verandering in de structuur ervoor zorgen dat het model slecht aansluit bij de dataset en daarom is het mogelijk dat de variantie van de residuen niet constant is.
• Wanneer sommige variabelen veel grotere waarden hebben dan de andere verklarende variabelen, kan het model heteroscedasticiteit hebben. In dit geval kunnen de variabelen worden gerelativeerd om het probleem op te lossen.

Sommige gevallen vertonen echter van nature waarschijnlijk heteroskedasticiteit. Als we bijvoorbeeld het inkomen van een persoon modelleren met zijn voedseluitgaven, hebben rijkere mensen een veel grotere variabiliteit in hun voedseluitgaven dan armere mensen. Omdat een rijk persoon soms in dure restaurants eet en andere keren in goedkope restaurants, in tegenstelling tot een arm persoon die altijd in goedkope restaurants eet. Daarom is het gemakkelijk voor het regressiemodel om heteroskedasticiteit te bezitten.

Gevolgen van heteroscedasticiteit

De gevolgen van heteroskedasticiteit in een regressiemodel zijn hoofdzakelijk als volgt:

• Efficiëntie gaat verloren in de kleinste kwadratenschatter, gedefinieerd als het gemiddelde van de kwadraten van de fouten.
• Er doen zich fouten voor bij de berekening van de covariantiematrix van de kleinste kwadratenschatters.

Correcte heteroscedasticiteit

Wanneer het resulterende regressiemodel heteroscedasticiteit is, kunnen we de volgende correcties proberen om heteroscedasticiteit te verkrijgen:

• Bereken de natuurlijke logaritme van de onafhankelijke variabele. Dit is over het algemeen handig als de variantie van de residuen in de grafiek toeneemt.
• Afhankelijk van de residuele grafiek kan een ander type transformatie van de onafhankelijke variabele praktischer zijn. Als de grafiek bijvoorbeeld de vorm heeft van een parabool, kunnen we het kwadraat van de onafhankelijke variabele berekenen en die variabele aan het model toevoegen.
• Voor het model kunnen ook andere variabelen worden gebruikt; door een variabele te verwijderen of toe te voegen, kan de variantie van de residuen worden gewijzigd.
• In plaats van het kleinste kwadratencriterium te gebruiken, kan het gewogen kleinste kwadratencriterium worden gebruikt.

Heteroscedasticiteit en homoscedasticiteit

Ten slotte zullen we zien wat de verschillen zijn tussen heteroscedasticiteit en homoscedasticiteit in de statistiek, aangezien dit twee concepten van regressiemodellen zijn waar we duidelijk over moeten zijn.

De homoscedasticiteit van een regressiemodel is een statistisch kenmerk dat aangeeft dat de foutvariantie constant is. Een homoscedastisch model betekent dus dat de variantie van zijn fouten constant is.

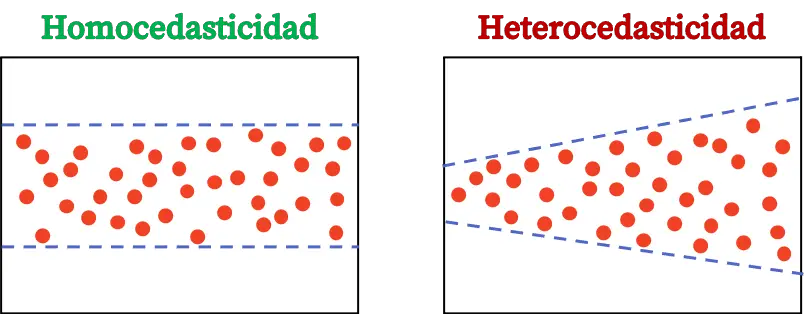
Het verschil tussen heteroscedasticiteit en homoskedasticiteit wordt gevonden in de constantheid van de variantie van de residuen. Als de variantie van de residuen van een model niet constant is, betekent dit dat het model heteroscedastisch is. Aan de andere kant, als de variantie van de residuen constant is, betekent dit dat deze homoscedastisch is.

Daarom moeten we ervoor zorgen dat het regressiemodel dat we bouwen homoscedastisch is, op deze manier zal aan de veronderstelling worden voldaan dat de variantie van de residuen constant is.