Histogrammen vergelijken (met voorbeelden)

Een histogram is een soort diagram waarmee we de verdeling van waarden in een reeks gegevens kunnen visualiseren.

De X-as toont de waarden van de dataset en de Y-as toont de frequentie van elke waarde.

Histogrammen zijn nuttig omdat ze ons in staat stellen snel de verdeling van waarden in een dataset te begrijpen. Ze zijn ook nuttig voor het vergelijken van twee verschillende datasets.

Wanneer we twee of meer histogrammen vergelijken, kunnen we drie verschillende vragen beantwoorden:

1. Hoe zijn de mediaanwaarden met elkaar te vergelijken?

We kunnen grofweg schatten dat de mediaan in het midden van elk histogram ligt, waardoor we de mediaanwaarden van de verdelingen kunnen vergelijken.

2. Hoe verhoudt de spreiding zich?

We kunnen visueel zien welk histogram meer verspreid is, wat ons een idee geeft van welke distributie meer verspreide waarden heeft.

3. Hoe verhoudt asymmetrie zich tot elkaar?

Als een histogram een „staart“ aan de linkerkant van de plot heeft, wordt er gezegd dat het negatief scheef is. Omgekeerd, als een histogram een „staart“ aan de rechterkant van de plot heeft, wordt er gezegd dat het positief scheef is. We kunnen elk histogram visueel controleren omde scheefheid te vergelijken.

Het volgende voorbeeld laat zien hoe u twee verschillende histogrammen kunt vergelijken en deze drie vragen kunt beantwoorden.

Voorbeeld: histogrammen vergelijken

Stel dat 200 studenten één studiemethode gebruiken om zich voor te bereiden op een examen en dat nog eens 200 studenten een andere studiemethode gebruiken om zich voor te bereiden op hetzelfde examen.

Stel dat we de volgende histogrammen maken om de examenresultaten van elke groep studenten te vergelijken:

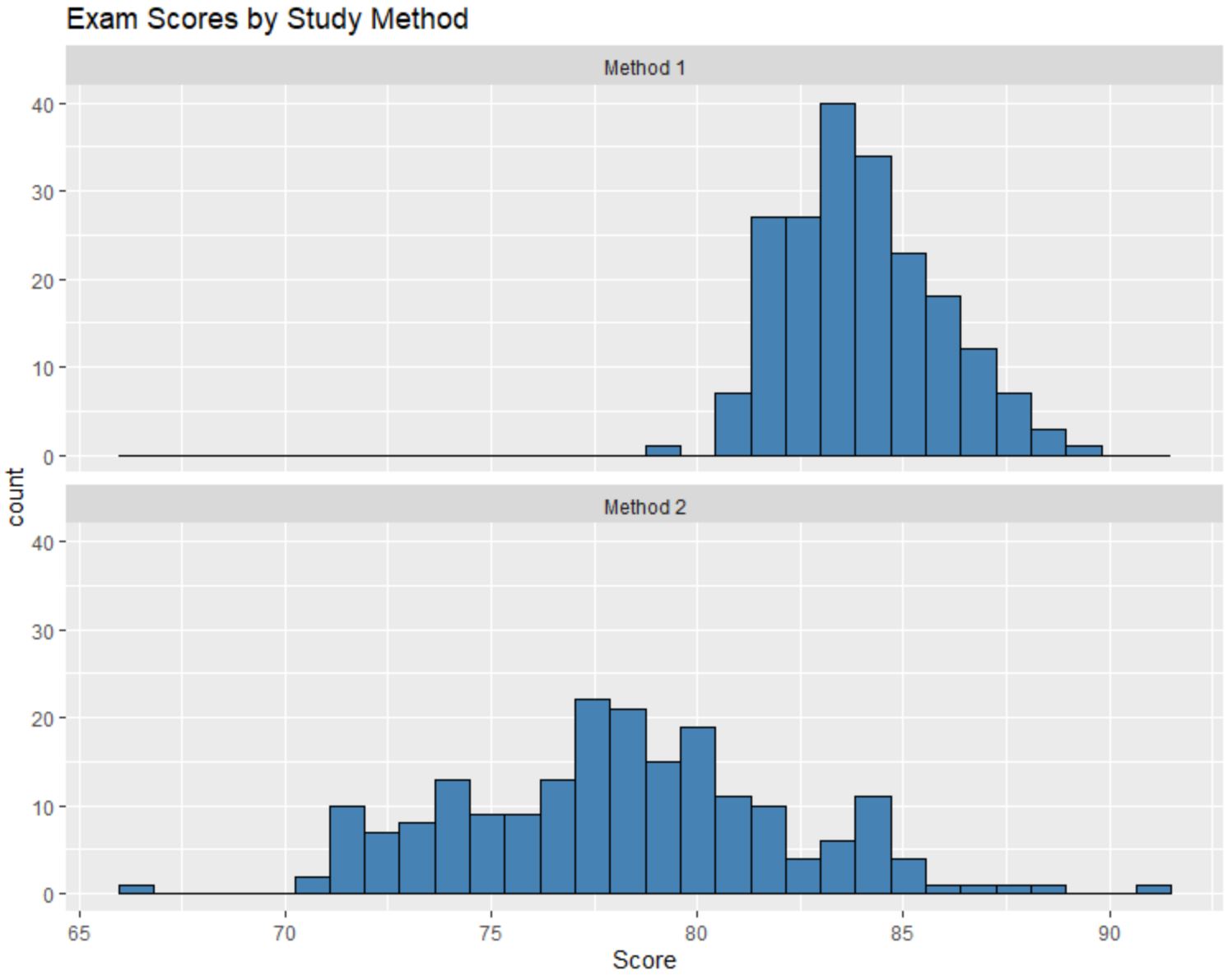
We kunnen deze histogrammen vergelijken en de volgende drie vragen beantwoorden:

1. Hoe zijn de mediaanwaarden met elkaar te vergelijken?

Hoewel we de exacte mediaanwaarden van elke verdeling niet kennen door simpelweg naar de histogrammen te kijken, is het duidelijk dat de mediane examenscore van studenten die Methode 1 gebruikten hoger is dan de mediane examenscore van studenten die Methode 1 gebruikten. methode 2.

We zouden kunnen schatten dat de mediaanwaarde voor methode 1 rond de 84 ligt en de mediaanwaarde voor methode 2 rond de 78.

2. Hoe verhoudt de spreiding zich?

De histogramwaarden voor Methode 2 zijn veel meer verspreid dan die voor Methode 1, wat ons vertelt dat er een veel grotere spreiding is in de examenresultaten voor studenten die Methode 2 gebruikten.

3. Hoe verhoudt asymmetrie zich tot elkaar?

Als we naar de histogrammen kijken, lijkt het erop dat de verdeling van de testscores voor methode 1 enigszins scheef naar rechts is, zoals aangegeven door de „staart“ die zich rechts van het histogram uitstrekt.

Er lijkt echter geen “staart” te zitten in de verdeling van examenresultaten voor methode 2, wat aangeeft dat de verdeling weinig of niet scheef is.

Bonus : hier is de code die we in R hebben gebruikt om deze twee histogrammen te maken:

 library (ggplot2)

#make this example reproducible
set. seeds (0)

#create data frame
df <- data. frame (method=rep(c(' Method 1 ', ' Method 2 '), each= 200 ),
                 Score=c(rnorm( 200 , mean= 84 , sd= 2 ),
                         rnorm( 200 , mean= 78 , sd= 4 )))

#create histogram of scores for each method
ggplot(df, aes(x=Score)) +
  geom_histogram(fill=' steelblue ', color=' black ') +
  facet_wrap(.~method, nrow= 2 ) +
  labs(title=' Exam Scores by Study Method ')

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere veelvoorkomende taken met histogrammen kunt uitvoeren:

Hoe u het gemiddelde en de mediaan van elk histogram kunt schatten
Hoe de standaardafwijking van elk histogram te schatten
Hoe de vorm van histogrammen te beschrijven