Hoe vif in excel te berekenen

Multicollineariteit bij regressieanalyse treedt op wanneer twee of meer verklarende variabelen sterk met elkaar gecorreleerd zijn, zodat ze geen unieke of onafhankelijke informatie verschaffen in het regressiemodel. Als de mate van correlatie tussen variabelen hoog genoeg is, kan dit problemen veroorzaken bij het aanpassen en interpreteren van het regressiemodel.

Gelukkig is het mogelijk om multicollineariteit te detecteren met behulp van een metriek genaamd variantie-inflatiefactor (VIF) , die de correlatie en sterkte van de correlatie tussen verklarende variabelen in een regressiemodel meet.

In deze tutorial wordt uitgelegd hoe u VIF in Excel berekent.

Voorbeeld: VIF berekenen in Excel

Voor dit voorbeeld zullen we meervoudige lineaire regressie uitvoeren met behulp van de volgende gegevensset die de kenmerken van 10 basketbalspelers beschrijft. We passen een regressiemodel toe met beoordeling als responsvariabele en punten, assists en rebounds als verklarende variabelen. Vervolgens zullen we de VIF-waarden voor elke verklarende variabele identificeren.

Stap 1: Voer meerdere lineaire regressie uit.

Ga op het bovenste lint naar het tabblad Gegevens en klik op Gegevensanalyse. Als u deze optie niet ziet, moet u eerst de gratis Analysis ToolPak-software installeren .

Zodra u op Data-analyse klikt, verschijnt een nieuw venster. Selecteer Regressie en klik op OK.

Vul de benodigde tabellen in voor de responsvariabelen en verklarende variabelen en klik vervolgens op OK.

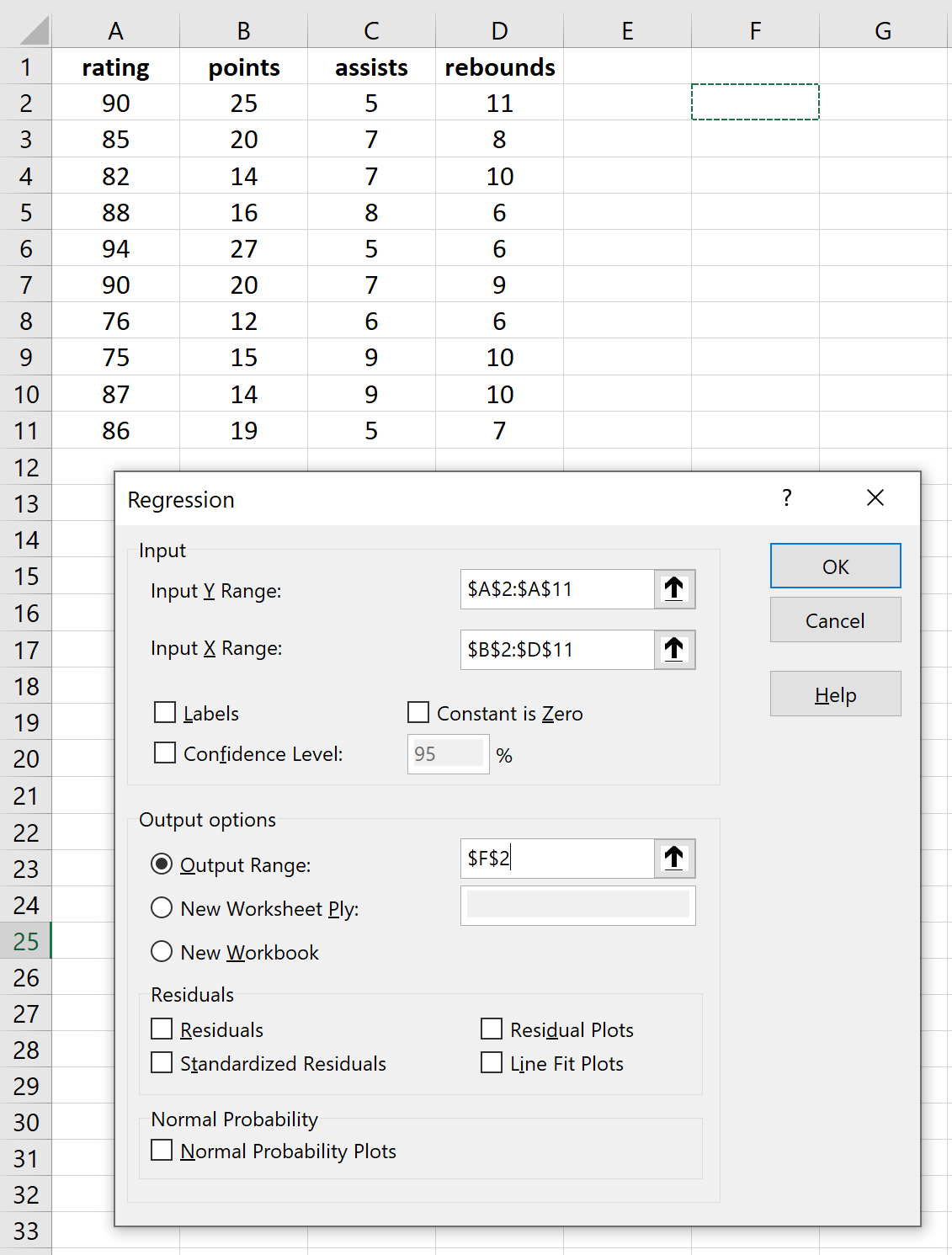
Dit levert het volgende resultaat op:

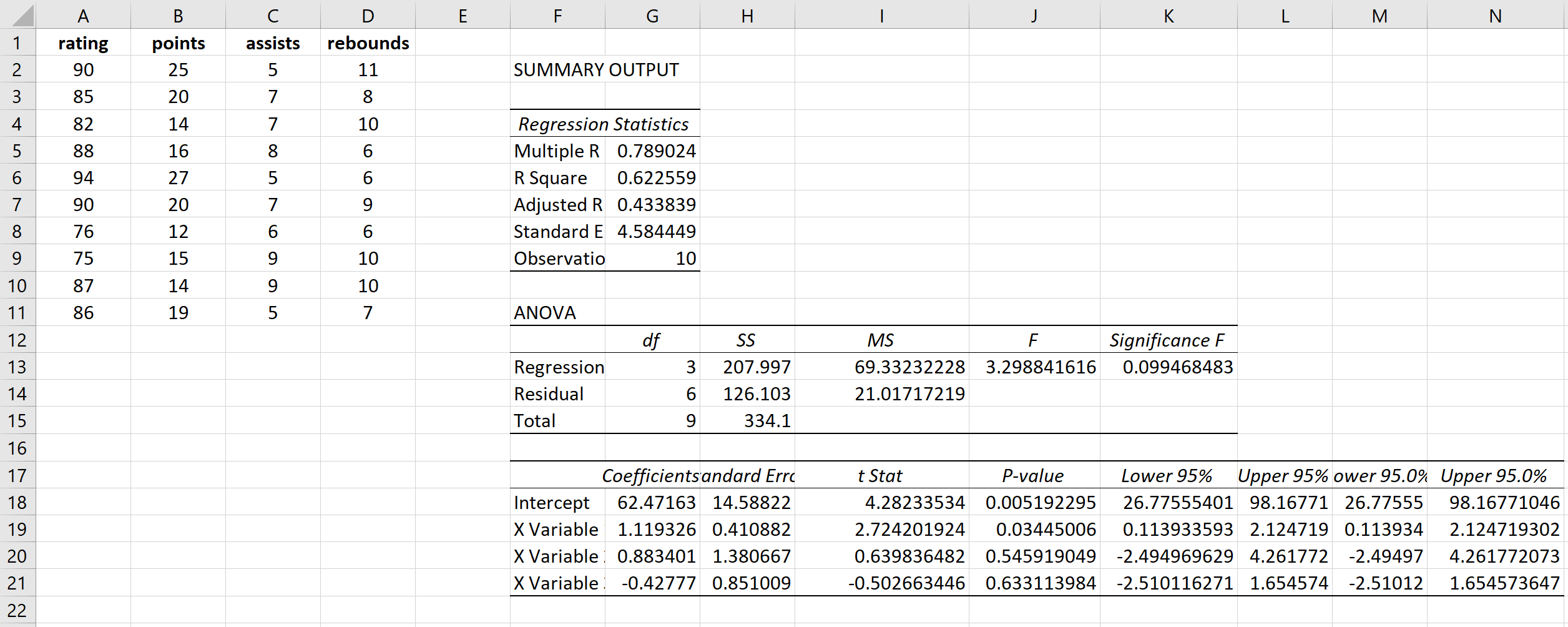
Stap 2: Bereken de VIF voor elke verklarende variabele.

Vervolgens kunnen we de VIF voor elk van de drie verklarende variabelen berekenen door individuele regressies uit te voeren met één verklarende variabele als responsvariabele en de andere twee als verklarende variabelen.

We kunnen bijvoorbeeld de VIF voor de puntenvariabele berekenen door een meervoudige lineaire regressie uit te voeren met punten als responsvariabele en assists en rebounds als verklarende variabelen.

Dit levert het volgende resultaat op:

De VIF voor punten wordt berekend als 1 / (1 – R Square) = 1 / (1 – .433099) = 1,76 .

We kunnen dit proces vervolgens herhalen voor de andere twee variabelen, assists en rebounds .

Het blijkt dat de VIF’s voor de drie verklarende variabelen als volgt zijn:

punten: 1,76
assists: 1.96
rebounds: 1.18

Hoe VIF-waarden te interpreteren

De VIF-waarde begint bij 1 en heeft geen bovengrens. Een algemene regel voor het interpreteren van VIF’s is:

• Een waarde van 1 geeft aan dat er geen correlatie bestaat tussen een bepaalde verklarende variabele en enige andere verklarende variabele in het model.
• Een waarde tussen 1 en 5 duidt op een gematigde correlatie tussen een bepaalde verklarende variabele en andere verklarende variabelen in het model, maar deze is vaak niet ernstig genoeg om speciale aandacht te vereisen.
• Een waarde groter dan 5 duidt op een potentieel ernstige correlatie tussen een bepaalde verklarende variabele en andere verklarende variabelen in het model. In dit geval zijn de coëfficiëntschattingen en p-waarden in de regressieresultaten waarschijnlijk onbetrouwbaar.

Omdat elk van de VIF-waarden van de verklarende variabelen in ons regressiemodel gesloten is op 1, is multicollineariteit in ons voorbeeld geen probleem.