Hoe de binomiale verdelingstabel te lezen

De binomiale verdelingstabel   is een tabel die de kansen toont die verband houden met de binominale verdeling . Om de binominale verdelingstabel te gebruiken, hebt u slechts drie waarden nodig:

• n: het aantal pogingen
• r: het aantal “successen” tijdens n pogingen
• p: de kans op succes van een bepaalde proef

Met behulp van deze drie getallen kunt u de binomiale verdelingstabel gebruiken om de kans te bepalen op het verkrijgen van precies r successen in de loop van n pogingen, wanneer de kans op succes bij elke poging p is.

De volgende voorbeelden illustreren hoe u de binomiale verdelingstabel leest.

voorbeeld 1

Vraag: Jessica maakt 60% van haar vrije worppogingen. Als ze zes vrije worpen maakt, wat is dan de kans dat ze er precies vier maakt?

Om deze vraag te beantwoorden, kunnen we in de binomiale verdelingstabel de waarde vinden die overeenkomt met n = 6, r = 4 en p = 0,60:

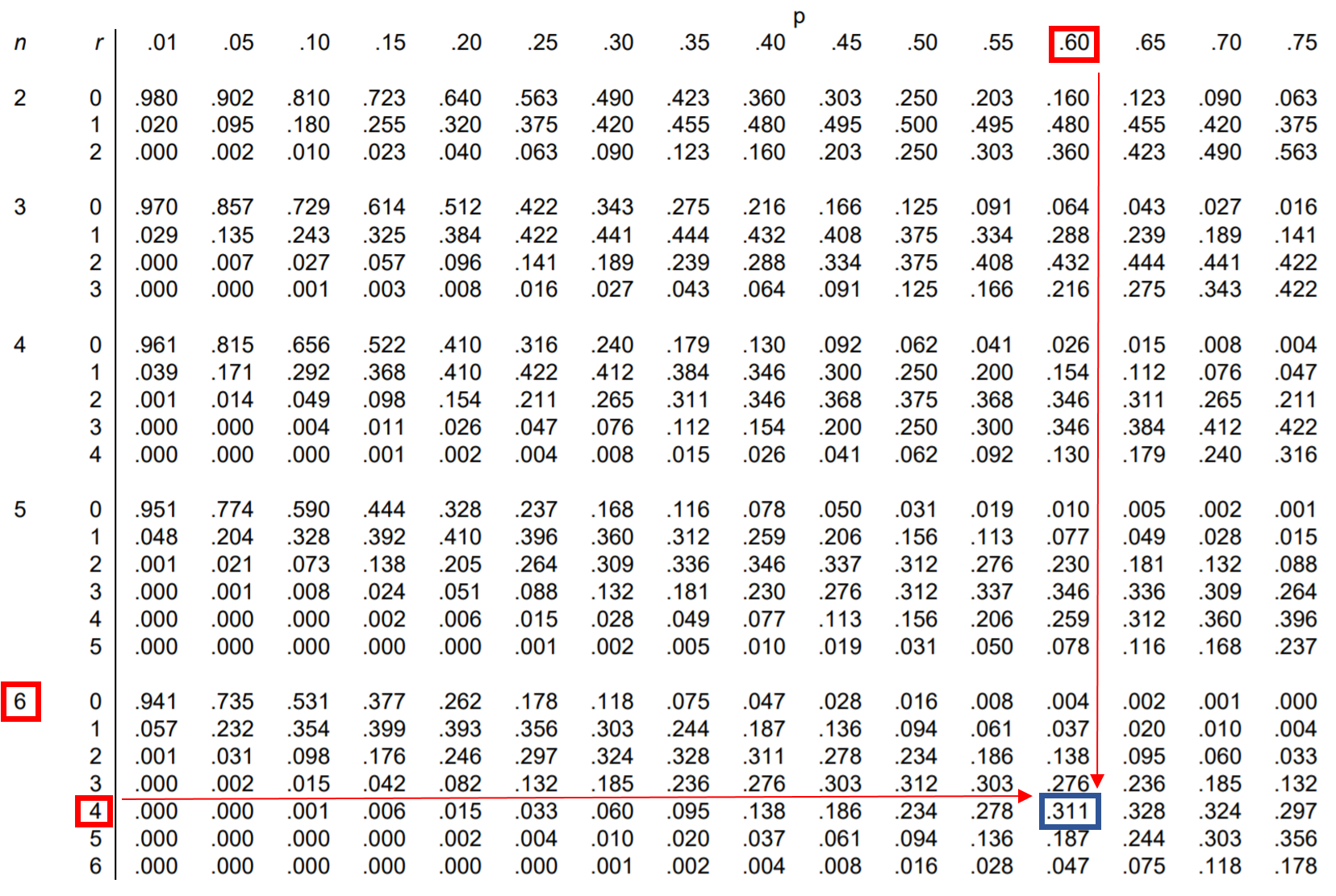
De kans dat Jessica precies 4 van de 6 vrije worpen maakt is 0,311 .

Voorbeeld 2

Vraag: Jessica maakt 60% van haar vrije worppogingen. Als ze zes vrije worpen maakt, wat is dan de kans dat ze er minder dan vier maakt?

Om deze waarschijnlijkheid te vinden, moet je eigenlijk de volgende kansen optellen:

P(maakt minder dan 4) = P(maakt 0) + P(maakt 1) + P(maakt 2) + P(maakt 3)

We kunnen dus elk van deze vier kansen opzoeken in de binomiale verdelingstabel en ze bij elkaar optellen:

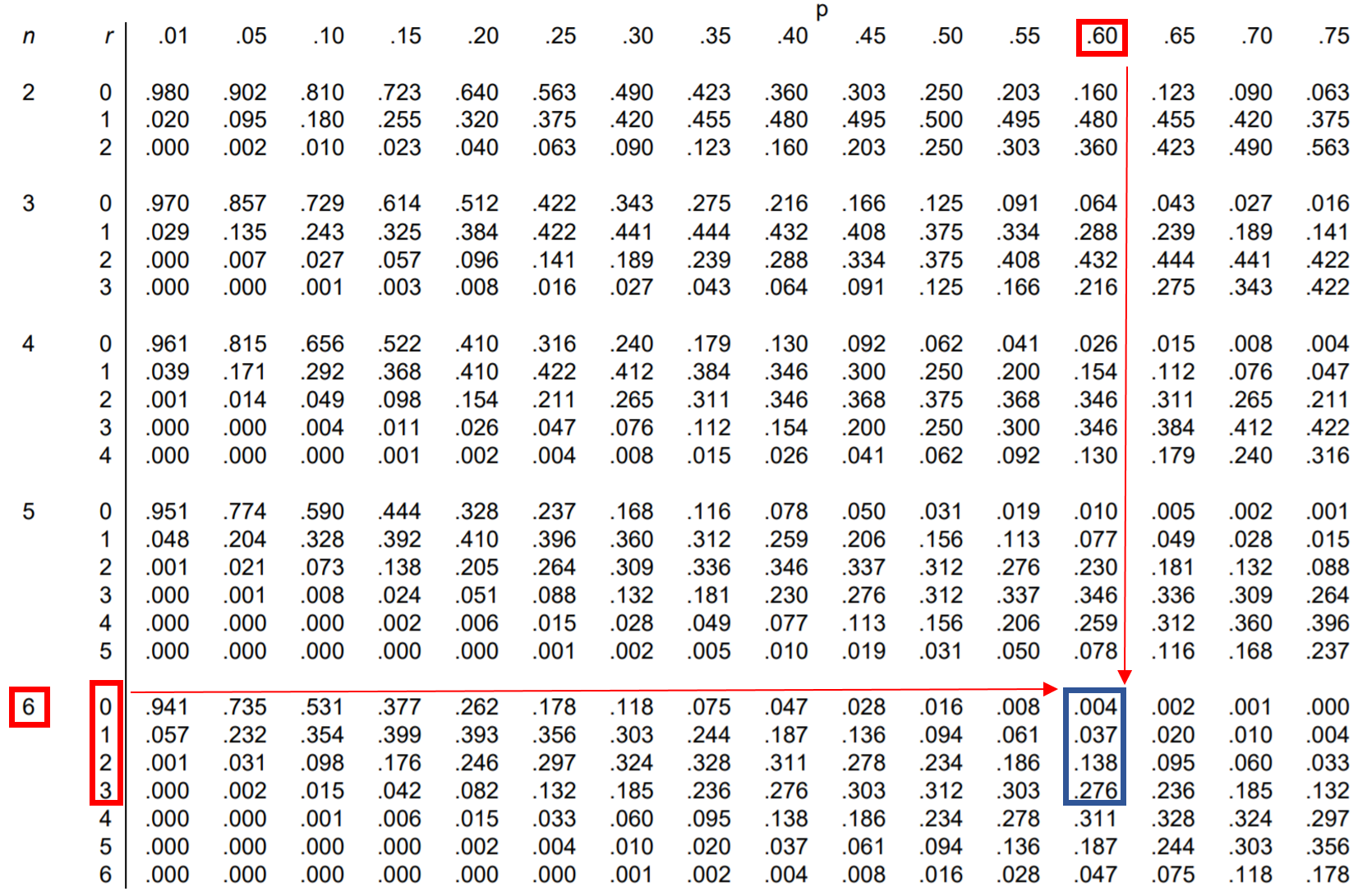
Uit de tabel blijkt dat P(kleiner is dan 4) = .004 + .037 + .138 + .276 = 0.455 .

De kans dat Jessica minder dan 4 vrije worpen maakt is 0,455 .

Voorbeeld 3

Vraag: Jessica maakt 60% van haar vrije worppogingen. Als ze zes vrije worpen maakt, wat is dan de kans dat ze er vier of meer maakt?

Om deze waarschijnlijkheid te vinden, moeten we de volgende kansen optellen:

P(maakt 4 of meer) = P(maakt 4) + P(maakt 5) + P(maakt 6)

We kunnen dus elk van deze drie kansen opzoeken in de binomiale verdelingstabel en ze bij elkaar optellen:

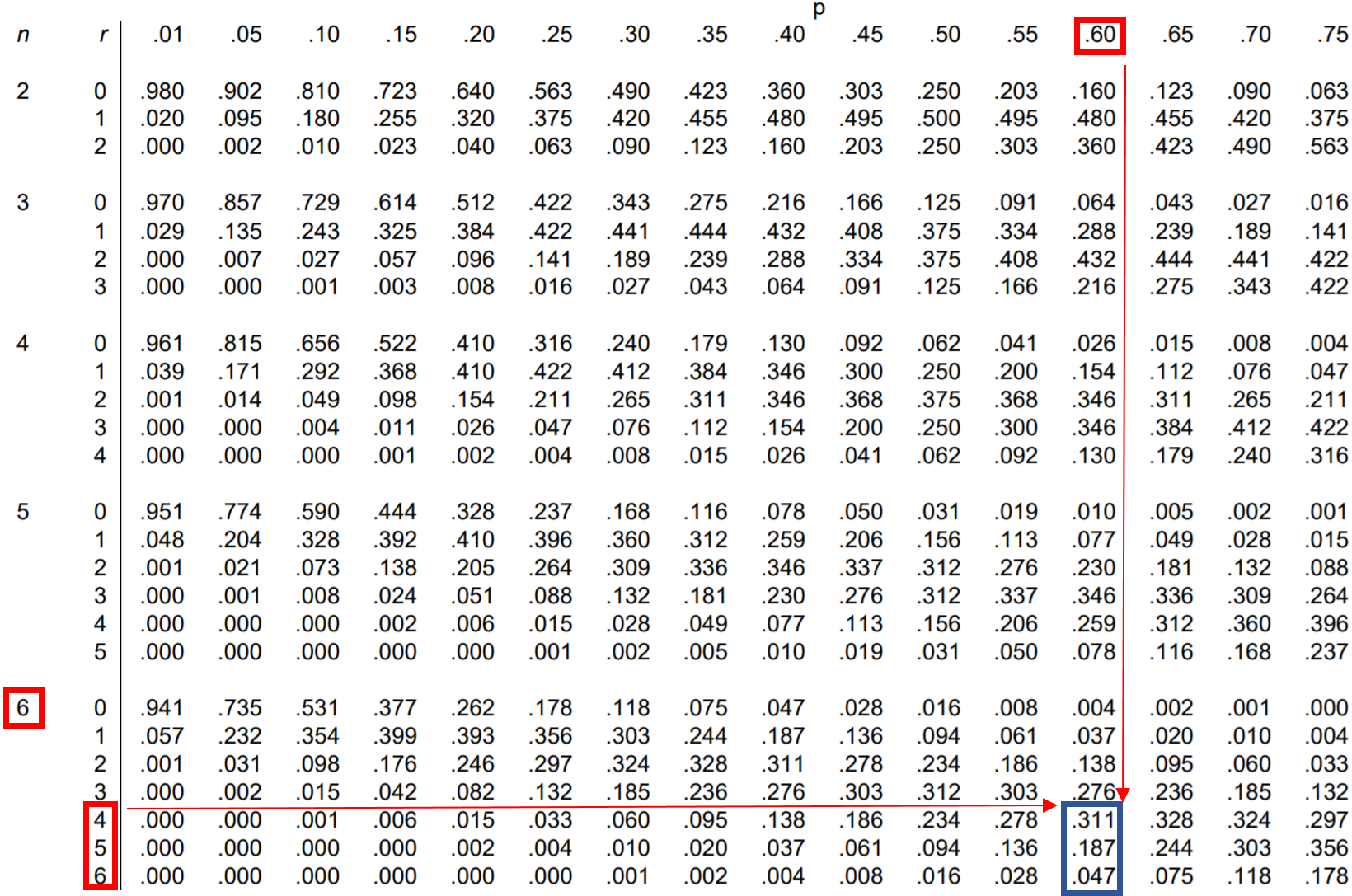
Uit de tabel blijkt dat P(maakt 4 of meer) = .311 + .187 + .047 = 0.545 .

De kans dat Jessica 4 of meer vrije worpen maakt is 0,545 .