Hoe een covariantiematrix te lezen

Covariantie is een maatstaf voor hoe veranderingen in één variabele verband houden met veranderingen in een tweede variabele. Meer specifiek is het een maatstaf voor de mate waarin twee variabelen lineair geassocieerd zijn.

Een covariantiematrix is een vierkante matrix die de covariantie tussen veel verschillende variabelen weergeeft. Dit kan een nuttige manier zijn om te begrijpen hoe verschillende variabelen in een dataset met elkaar samenhangen.

Het volgende voorbeeld laat zien hoe u een covariantiematrix in de praktijk kunt lezen.

Hoe een covariantiematrix te lezen

Stel dat we de volgende covariantiematrix hebben die informatie bevat over examenscores voor drie verschillende vakken voor studenten:

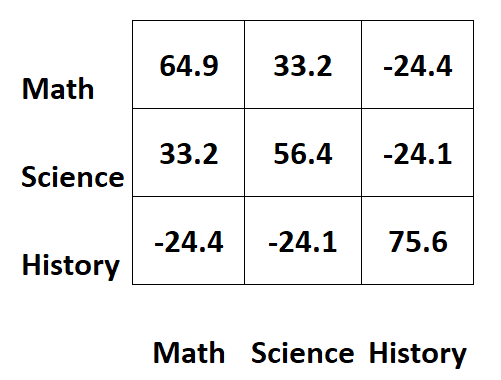
De waarden langs de diagonalen van de matrix vertegenwoordigen de varianties van elk onderwerp.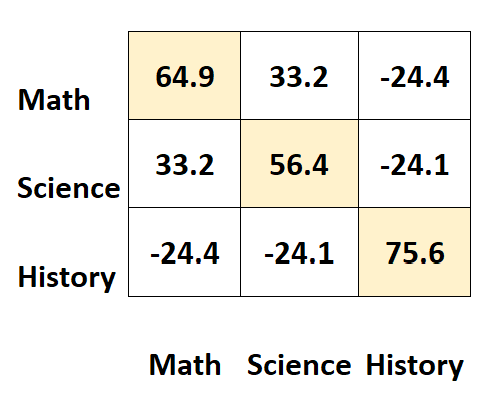

Bijvoorbeeld:

• De variantie van de wiskunderesultaten is 64,9 .
• De variantie van wetenschapsscores is 56,4 .
• De variantie van historische scores is 75,6 .

De overige waarden van de matrix vertegenwoordigen de covarianties tussen de verschillende onderwerpen.

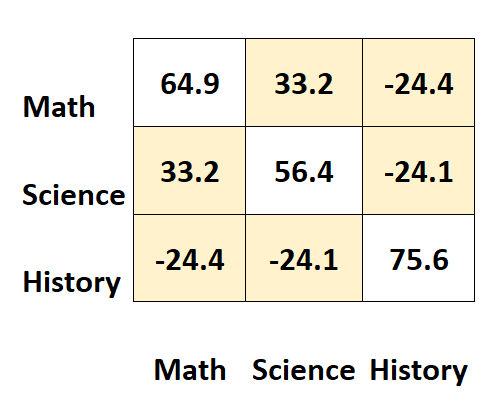
Bijvoorbeeld:

• De covariantie tussen wiskunde- en natuurwetenschappenscores is 33,2 .
• De covariantie tussen wiskunde- en geschiedenisscores is –24,4 .
• De covariantie tussen wetenschaps- en geschiedenisscores is –24,1 .

Een positief getal voor covariantie geeft aan dat twee variabelen de neiging hebben om tegelijkertijd te stijgen of dalen.

Wiskunde en natuurwetenschappen hebben bijvoorbeeld een positieve covariantie ( 33,2 ), wat aangeeft dat leerlingen die hoog scoren op wiskunde ook vaak hoog scoren op natuurwetenschappen.

Omgekeerd presteren leerlingen die slecht presteren in de wiskunde ook vaak slecht in de natuurwetenschappen.

Een negatief getal voor covariantie geeft aan dat naarmate één variabele toeneemt, een tweede variabele de neiging heeft af te nemen.

Wiskunde en geschiedenis hebben bijvoorbeeld een negatieve covariantie ( -24,44 ), wat aangeeft dat leerlingen die hoog presteren in wiskunde doorgaans laag presteren in geschiedenis.

Omgekeerd scoren leerlingen die laag scoren op wiskunde doorgaans hoog op geschiedenis.

Een opmerking over de symmetrie van een covariantiematrix

Opgemerkt moet worden dat een covariantiematrix perfect symmetrisch is.

De cel rechtsboven toont bijvoorbeeld exact dezelfde waarde als de cel linksonder:

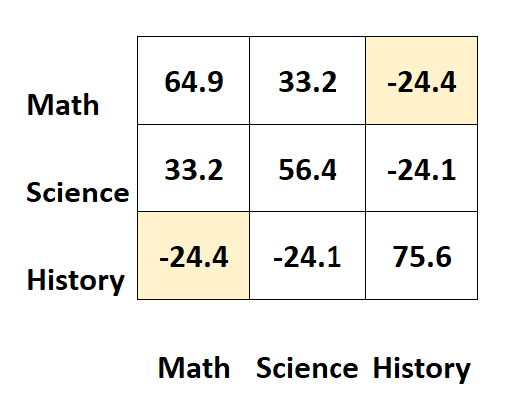
De twee cellen meten inderdaad de covariantie tussen geschiedenis en wiskunde.

Omdat een covariantiematrix symmetrisch is, is de helft van de covariantiewaarden die in de matrix worden weergegeven overbodig en onnodig.

Soms wordt dus slechts de helft van de covariantiematrix weergegeven:

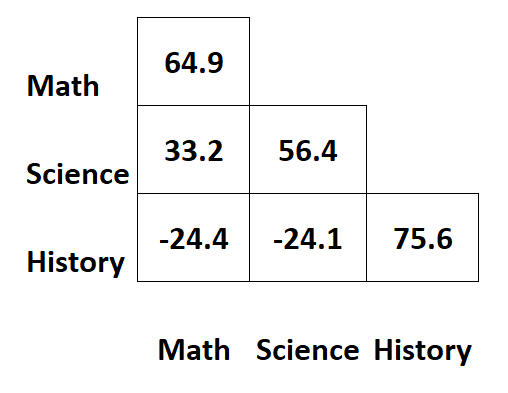
Wanneer moet u een covariantiematrix gebruiken?

In de praktijk zul je vaker een correlatiematrix moeten maken en interpreteren dan een covariantiematrix.

Covariantiematrices worden echter vaak ‘onder de motorkap’ gebruikt voor verschillende machine learning-algoritmen en -modellen.

De covariantiematrix wordt bijvoorbeeld gebruikt tijdens de analyse van hoofdcomponenten , wat ons helpt de onderliggende patronen te begrijpen in een dataset die een groot aantal variabelen bevat.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u een covariantiematrix maakt met behulp van verschillende statistische software:

Hoe maak je een covariantiematrix in R
Hoe u een covariantiematrix in Python maakt
Hoe u een covariantiematrix maakt in SPSS
Hoe u een covariantiematrix maakt in Excel