Hoe de resterende standaardfout te interpreteren

De resterende standaardfout wordt gebruikt om te meten hoe goed een regressiemodel bij een dataset past.

In eenvoudige bewoordingen meet het de standaardafwijking van residuen in een regressiemodel.

Het wordt als volgt berekend:

Residuele standaardfout = √ Σ(y – ŷ) ² /df

Goud:

• y: De waargenomen waarde
• ŷ: De voorspelde waarde
• df: De vrijheidsgraden, berekend als het totale aantal waarnemingen – totaal aantal modelparameters.

Hoe kleiner de resterende standaardfout, hoe beter een regressiemodel bij een dataset past. Omgekeerd geldt: hoe hoger de resterende standaardfout, hoe slechter het regressiemodel bij een dataset past.

Een regressiemodel met een kleine resterende standaardfout heeft gegevenspunten die strak geclusterd zijn rond de aangepaste regressielijn:

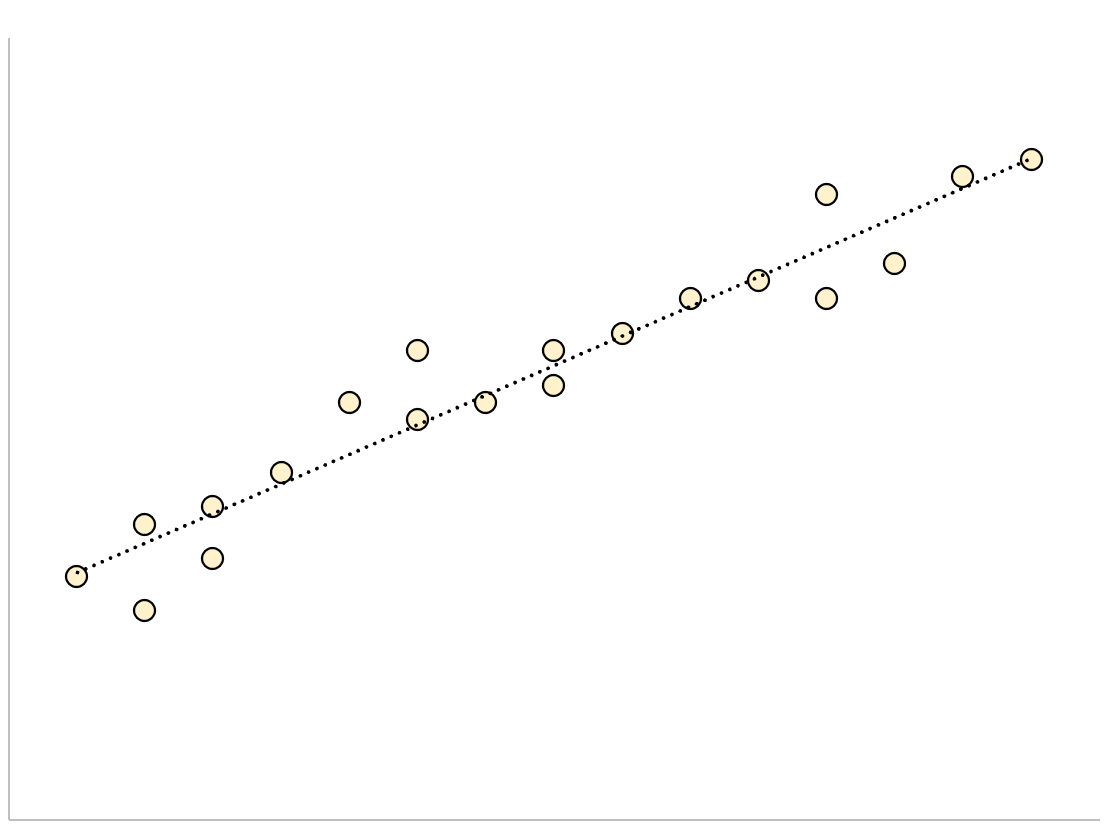
De residuen van dit model (het verschil tussen de waargenomen waarden en de voorspelde waarden) zullen klein zijn, wat betekent dat de resterende standaardfout ook klein zal zijn.

Omgekeerd zal een regressiemodel met een grote resterende standaardfout de gegevenspunten losser verspreid hebben rond de aangepaste regressielijn:

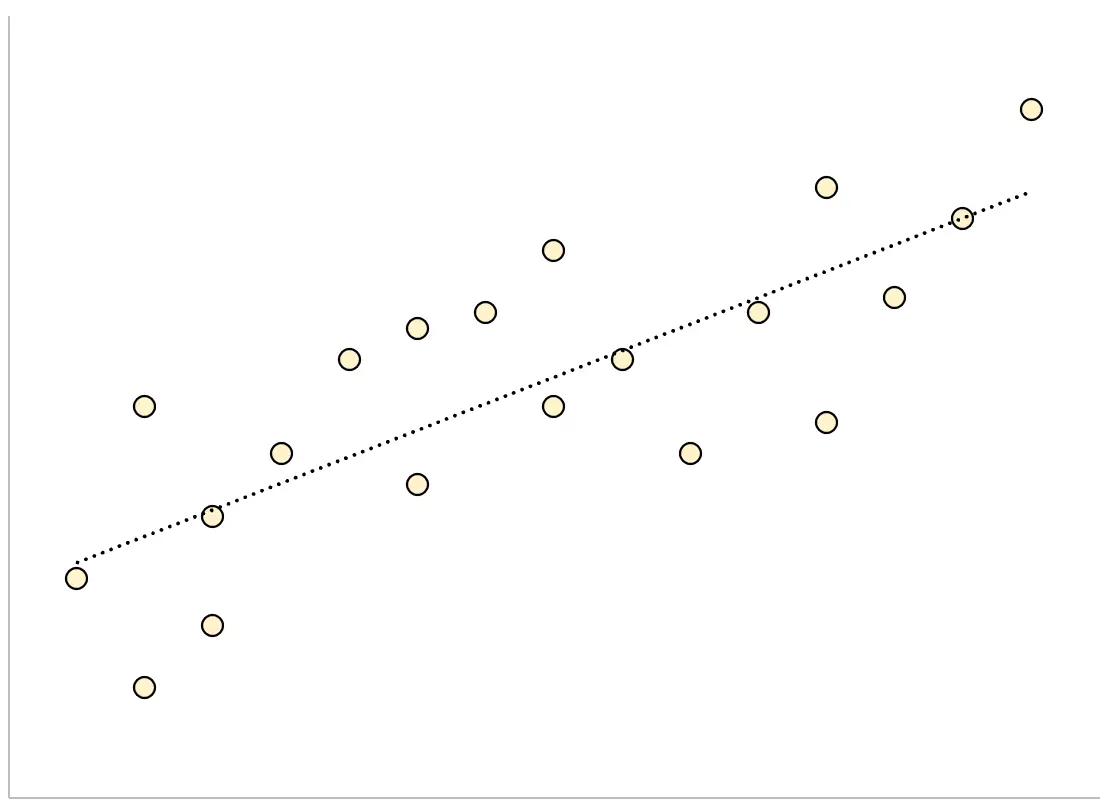
De residuen uit dit model zullen groter zijn, wat betekent dat de residuele standaardfout ook groter zal zijn.

Het volgende voorbeeld laat zien hoe u de resterende standaardfout van een regressiemodel in R kunt berekenen en interpreteren.

Voorbeeld: interpretatie van de resterende standaardfout

Stel dat we willen passen in het volgende meervoudige lineaire regressiemodel:

mpg = β ₀ + β ₁ (verplaatsing) + β ₂ (vermogen)

Dit model gebruikt de voorspellende variabelen ‘verplaatsing’ en ‘pk’ om het aantal kilometers per gallon te voorspellen dat een bepaalde auto aflegt.

De volgende code laat zien hoe dit regressiemodel in R past:

 #load built-in mtcars dataset
data(mtcars)

#fit regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Call:
lm(formula = mpg ~ disp + hp, data = mtcars)

Residuals:
    Min 1Q Median 3Q Max 
-4.7945 -2.3036 -0.8246 1.8582 6.9363 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

Helemaal onderaan het resultaat kunnen we zien dat de resterende standaardfout van dit model 3,127 bedraagt.

Dit vertelt ons dat het regressiemodel auto-mpg voorspelt met een gemiddelde fout van ongeveer 3.127.

Gebruik van de resterende standaardfout om modellen te vergelijken

De resterende standaardfout is vooral handig voor het vergelijken van de fit van verschillende regressiemodellen.

Stel dat we twee verschillende regressiemodellen gebruiken om de mpg van auto’s te voorspellen. De resterende standaardfout van elk model is als volgt:

• Resterende standaardfout van model 1: 3,127
• Resterende standaardfout van model 2: 5,657

Omdat Model 1 een lagere resterende standaardfout heeft, past het beter bij de gegevens dan Model 2. We zouden Model 1 dus liever gebruiken om de mpg van auto’s te voorspellen, omdat de voorspellingen die het doet dichter bij de waargenomen mpg-waarden van auto’s liggen.

Aanvullende bronnen

Hoe eenvoudige lineaire regressie uit te voeren in R
Hoe meervoudige lineaire regressie uit te voeren in R
Hoe maak je een restplot in R