Hoe de z-tabel te gebruiken (met voorbeelden)

Een z-tabel is een tabel die je vertelt welk percentage waarden onder een bepaalde z-score valt in een standaard normale verdeling.

Een z-score vertelt u eenvoudigweg hoeveel standaarddeviaties een individuele gegevenswaarde van het gemiddelde afwijkt. Het wordt als volgt berekend:

z-score = (x – μ) / σ

Goud:

• x: individuele gegevenswaarde
• μ: populatiegemiddelde
• σ: standaarddeviatie van de populatie

Deze tutorial toont verschillende voorbeelden van het gebruik van de z-tabel.

voorbeeld 1

Scores op een bepaald toelatingsexamen voor een universiteit zijn normaal verdeeld met gemiddelde μ = 82 en standaarddeviatie σ = 8. Hoeveel procent van de studenten scoort ongeveer lager dan 84 op het examen?

Stap 1: Zoek de z-score.

Eerst vinden we de z-score die hoort bij een examenscore van 84:

z-score = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0,25

Stap 2: Gebruik het z-diagram om het percentage te vinden dat overeenkomt met de z-score.

Vervolgens gaan we op zoek naar de waarde 0,25 in de z-tabel:

Ongeveer 59,87% van de studenten scoort op dit examen lager dan 84.

Voorbeeld 2

De hoogte van planten in een bepaalde tuin is normaal verdeeld met een gemiddelde van μ = 26,5 inch en een standaardafwijking van σ = 2,5 inch. Hoeveel procent van de planten is ongeveer 60 cm hoog?

Stap 1: Zoek de z-score.

Eerst zullen we de z-score vinden die hoort bij een hoogte van 26 inch.

z-score = (x – μ) / σ = (26 – 26,5) / 2,5 = -0,5 / 2,5 = -0,2

Stap 2: Gebruik het z-diagram om het percentage te vinden dat overeenkomt met de z-score.

Vervolgens gaan we op zoek naar de waarde -0,2   in tabel z:

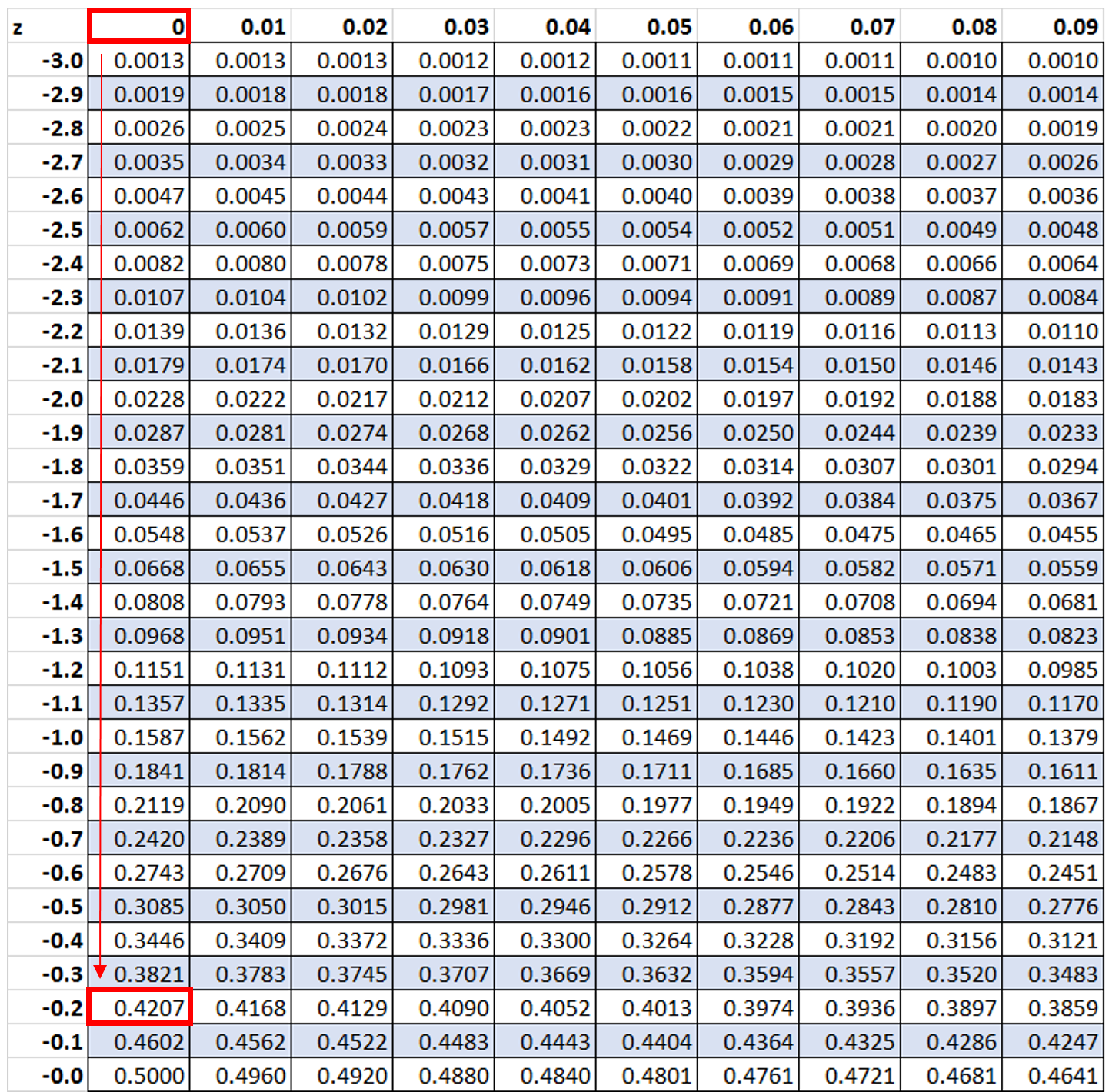
We zien dat 42,07% van de waarden onder een z-score van -0,2 liggen. In dit voorbeeld willen we echter weten welk percentage van de waarden groter is dan -0,2, wat we kunnen vinden met de formule 100% – 42,07% = 57,93%.

Ongeveer 59,87% van de planten in deze tuin is dus meer dan 60 cm hoog.

Voorbeeld 3

Het gewicht van een bepaalde dolfijnensoort is normaal verdeeld met een gemiddelde van μ = 400 pond en een standaardafwijking van σ = 25 pond. Hoeveel procent van de dolfijnen weegt ongeveer tussen de 410 en 425 pond?

Stap 1: Zoek de z-scores.

Eerst zullen we de z-scores vinden die horen bij 410 boeken en 425 boeken

z-score van 410 = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0,4

z-score van 425 = (x – μ) / σ = (425 – 400) / 25 = 25 / 25 = 1

Stap 2: Gebruik het z-diagram om de percentages te vinden die overeenkomen met elke z-score.

Eerst gaan we op zoek naar de waarde 0,4   in tabel z:

Vervolgens gaan we op zoek naar de waarde 1   in tabel z:

Ten slotte trekken we de kleinste waarde af van de grootste waarde: 0,8413 – 0,6554 = 0,1859 .

Ongeveer 18,59% van de dolfijnen weegt dus tussen de 410 en 425 pond.

Aanvullende bronnen

Een inleiding tot de normale verdeling
Berekening van het normale verspreidingsgebied
Z-score rekenmachine