Hoe de chi-kwadraatverdelingstabel te lezen

In deze tutorial wordt uitgelegd hoe u het Chi-kwadraatverdelingsdiagram leest en interpreteert.

Wat is de chi-kwadraatverdelingstabel?

De Chi-kwadraatverdelingstabel is een tabel die de kritische waarden van de Chi-kwadraatverdeling weergeeft. Om de Chi-kwadraatverdelingstabel te gebruiken, hoeft u slechts twee waarden te kennen:

• Vrijheidsgraden voor de Chi-kwadraattoets
• Het alfaniveau van de test (veel voorkomende keuzes zijn 0,01, 0,05 en 0,10)

De volgende afbeelding toont de eerste 20 rijen van de Chi-kwadraatverdelingstabel, met vrijheidsgraden aan de linkerkant van de tabel en alfaniveaus bovenaan de tabel:

Let op: Hier vindt u een volledige Chi-kwadraatverdelingstabel met meer vrijheidsgraden.

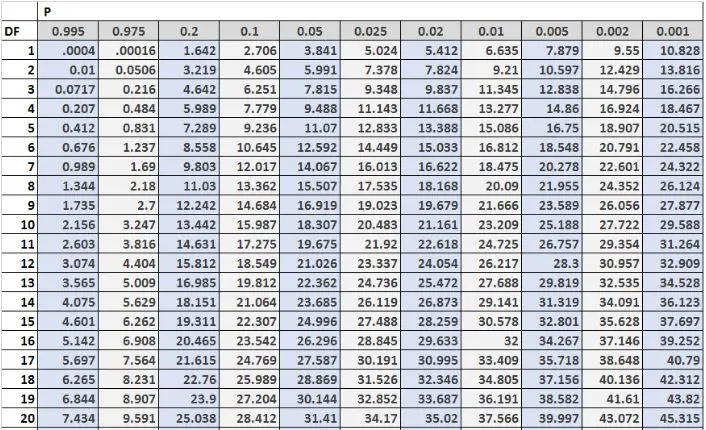
De kritische waarden in de tabel worden vaak vergeleken met de teststatistieken van een Chi-kwadraattoets. Als de teststatistiek groter is dan de kritische waarde in de tabel, kun je de nulhypothese van de Chi-kwadraattoets verwerpen en concluderen dat de testresultaten statistisch significant zijn.

Voorbeelden van het gebruik van de chikwadraatverdelingstabel

We laten zien hoe u de Chi-kwadraatverdelingstabel kunt gebruiken met de volgende drie soorten Chi-kwadraattoetsen:

• Chi-kwadraattoets voor onafhankelijkheid
• Chi-kwadraattest voor de goede pasvorm
• Chikwadraattest voor homogeniteit

Chi-kwadraattoets voor onafhankelijkheid

We gebruiken een Chi-kwadraattoets voor onafhankelijkheid als we willen testen of er al dan niet een significant verband bestaat tussen twee categorische variabelen.

Voorbeeld: Stel dat we willen weten of gender wel of niet geassocieerd is met de voorkeur voor een politieke partij. We nemen een eenvoudige willekeurige steekproef van 500 kiezers en vragen hen naar hun politieke partijvoorkeur. Met een significantieniveau van 0,05 voeren we een chikwadraattoets uit om te bepalen of geslacht geassocieerd is met politieke partijvoorkeur. De volgende tabel geeft de resultaten van het onderzoek weer:

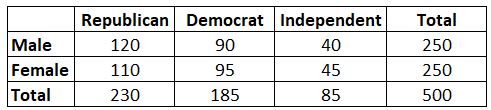
Het blijkt dat de teststatistiek voor deze Chi-kwadraattest 0,864 is.

Vervolgens kunnen we de kritische testwaarde vinden in de Chi-kwadraatverdelingstabel. De vrijheidsgraden zijn gelijk aan (#rijen-1) * (#kolommen-1) = (2-1) * (3-1) = 2 en het probleem vertelde ons dat we een alfaniveau van 0,05 moesten gebruiken. Dus, volgens de Chi-kwadraatverdelingstabel is de kritische waarde van de test 5,991 .

Omdat onze teststatistiek lager is dan onze kritische waarde, slagen we er niet in de nulhypothese te verwerpen. Dit betekent dat we niet voldoende bewijs hebben om te zeggen dat er een verband bestaat tussen geslacht en politieke partijvoorkeuren.

Chi-kwadraattest voor de goede pasvorm

We gebruiken een chikwadraat- goodness-of-fit-test als we willen testen of een categorische variabele al dan niet een hypothetische verdeling volgt.

Voorbeeld: Een winkeleigenaar zegt dat 30% van al zijn weekendklanten op vrijdag komt, 50% op zaterdag en 20% op zondag. Een onafhankelijke onderzoeker bezoekt de winkel in een willekeurig weekend en vindt 91 klanten op vrijdag, 104 op zaterdag en 65 op zondag. Met een significantieniveau van 0,10 voeren we een chikwadraattest uit om de goede pasvorm te controleren en te bepalen of de gegevens consistent zijn met de bewering van de winkeleigenaar.

In dit geval blijkt de teststatistiek 10.616 te zijn.

Vervolgens kunnen we de kritische testwaarde vinden in de Chi-kwadraatverdelingstabel. De vrijheidsgraden zijn gelijk aan (#outcomes-1) = 3-1 = 2 en het probleem vertelt ons dat we een alfaniveau van 0,10 moeten gebruiken. Volgens de Chi-kwadraatverdelingstabel is de kritische waarde van de test dus 4,605 .

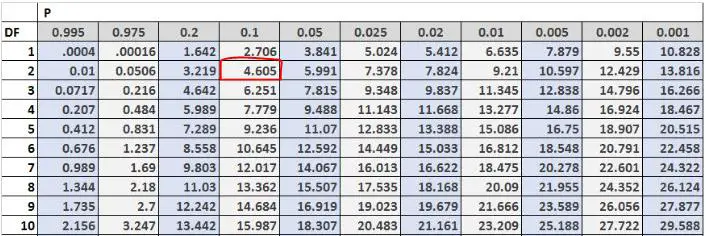
Omdat onze teststatistiek groter is dan onze kritische waarde, verwerpen we de nulhypothese. Dit betekent dat we voldoende bewijs hebben om te zeggen dat de werkelijke verdeling van klanten die in het weekend naar deze winkel komen niet gelijk is aan 30% op vrijdag, 50% op zaterdag en 20% op zondag.

Chikwadraattest voor homogeniteit

We gebruiken een Chi-kwadraattoets voor homogeniteit als we formeel willen testen of er al dan niet een verschil is in verhoudingen tussen meerdere groepen.

Voorbeeld: Een basketbaltrainingscentrum wil kijken of twee nieuwe trainingsprogramma’s het aandeel spelers dat slaagt voor een moeilijke schietproef verbeteren. 172 spelers worden willekeurig toegewezen aan programma 1, 173 aan programma 2 en 215 aan het huidige programma. Na een maand gebruik te hebben gemaakt van de trainingsprogramma’s, doen de spelers vervolgens een schietproef. De onderstaande tabel toont het aantal spelers dat slaagt voor de schiettest, op basis van het programma dat ze gebruikten.

Met een significantieniveau van 0,05 voeren we een chikwadraattoets uit om te bepalen of het slagingspercentage voor elk trainingsprogramma hetzelfde is.

Het blijkt dat de teststatistiek voor deze Chi-kwadraattest 4,208 is.

Vervolgens kunnen we de kritische testwaarde vinden in de Chi-kwadraatverdelingstabel. De vrijheidsgraden zijn gelijk aan (#rijen-1) * (#kolommen-1) = (2-1) * (3-1) = 2 en het probleem vertelde ons dat we een alfaniveau van 0,05 moesten gebruiken. Dus, volgens de Chi-kwadraatverdelingstabel is de kritische waarde van de test 5,991 .

Omdat onze teststatistiek lager is dan onze kritische waarde, slagen we er niet in de nulhypothese te verwerpen. Dit betekent dat we niet voldoende bewijs hebben om te zeggen dat de drie trainingsprogramma’s verschillende resultaten opleveren.