Een boxplot met uitschieters lezen (met voorbeeld)

Een boxplot is een type plot dat de vijfcijferige samenvatting van een dataset weergeeft, waaronder:

• De minimumwaarde
• Het eerste kwartiel (het 25e percentiel)
• De gemiddelde waarde
• Het derde kwartiel (het 75e percentiel)
• De maximale waarde

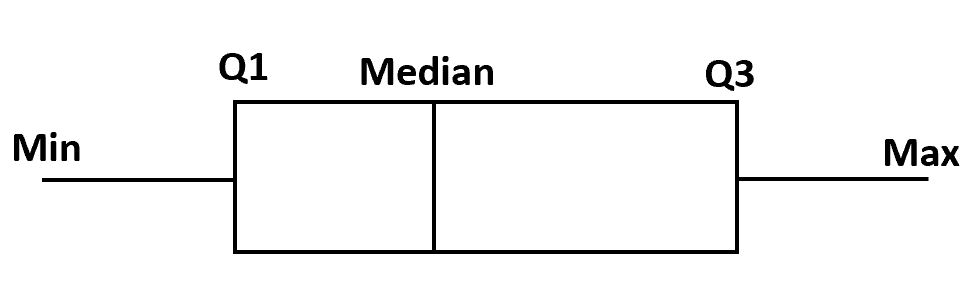
Om een boxplot te maken, tekenen we eerst een box van het eerste tot en met het derde kwartiel.

Vervolgens tekenen we een verticale lijn op de mediaan.

Ten slotte tekenen we ‘snorharen’ van de kwartielen tot aan de minimale en maximale waarde.

In de meeste statistische software wordt een waarneming gedefinieerd als een uitbijter als deze aan een van de volgende twee vereisten voldoet:

• De waarneming is 1,5 keer de interkwartielafstand onder het eerste kwartiel (Q1)
• De waarneming is 1,5 keer de interkwartielafstand boven het derde kwartiel (Q3).

Als er een uitschieter bestaat in een dataset, wordt deze gewoonlijk gelabeld met een klein puntje buiten het snorhaarbereik in de boxplot:

Wanneer dit gebeurt, worden aan de ‘minimum’- en ‘maximum’-waarden in de boxplot eenvoudigweg de waarden Q1 – 1,5*IQR en Q3 + 1,5*IQR toegewezen.

Het volgende voorbeeld laat zien hoe boxplots met en zonder uitbijters moeten worden geïnterpreteerd.

Voorbeeld: een boxplot met uitschieters interpreteren

Stel dat we de volgende twee boxplots maken om de verdeling van de punten gescoord door basketbalspelers van twee verschillende teams te visualiseren:

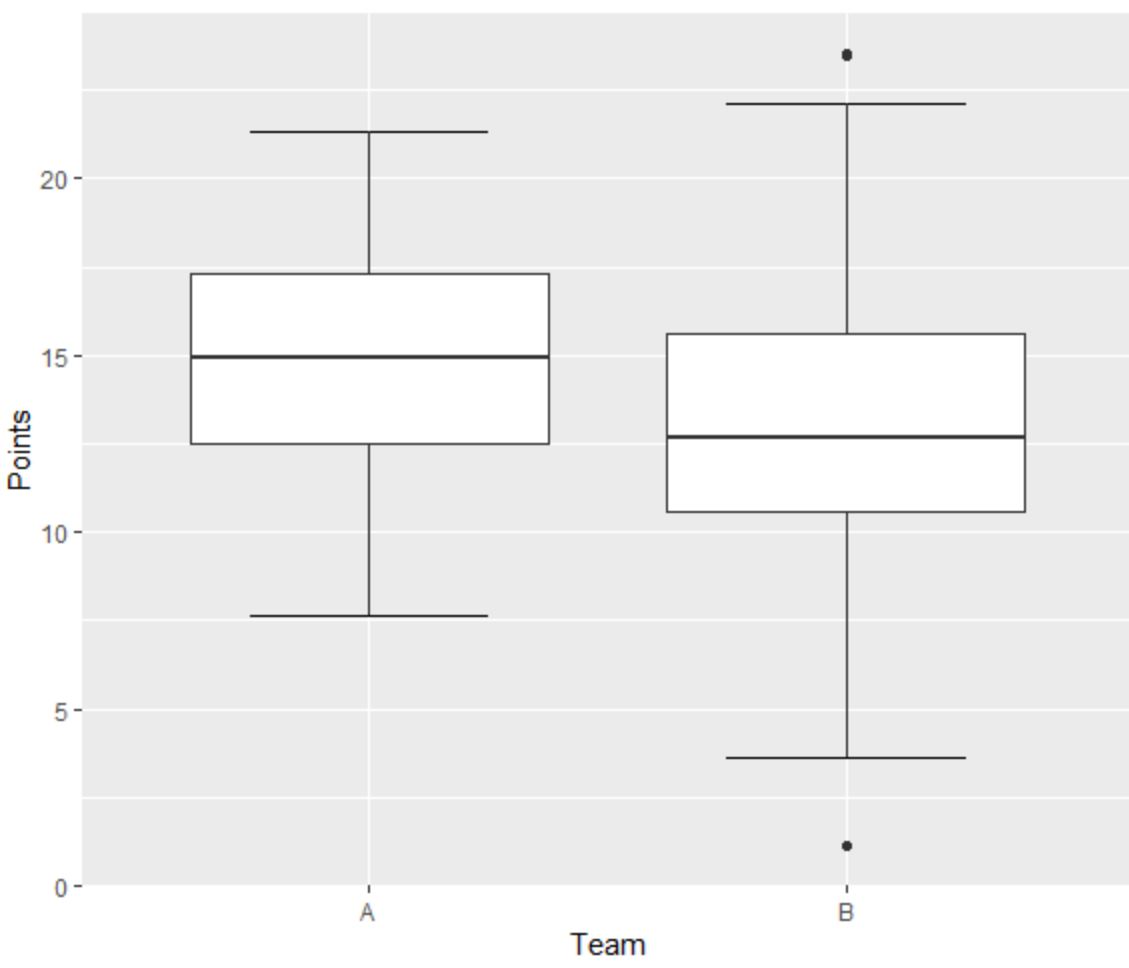
De linkerboxplot voor team A heeft geen uitschieters, aangezien er geen kleine puntjes buiten de minimum- of maximumwhisker liggen.

De rechter boxplot voor team B heeft echter één uitbijter boven de „maximale“ waarde en één uitbijter onder de „minimale“ waarde.

Hier is het huidige vijfcijferige overzicht van de verdeling van de variabele “Punten” voor Team B:

• Minimumwaarde: 1.1
• Eerste kwartiel: 10,5
• Mediaan: 12,7
• Derde kwartiel: 15,6
• Maximale waarde: 23,5

Zo berekent u de limieten van potentiële uitschieters:

Interkwartielschaal : Derde kwartiel – Eerste kwartiel = 15,6 – 10,5 = 5,1

Ondergrens : Q1 – 1,5*IQR = 10,5 – 1,5*5,1 = 2,85

Bovengrens : Q3 + 1,5*IQR = 15,6 + 1,5*5,1 = 23,25

De snorharen voor de minimum- en maximumwaarden in de boxplot zijn geplaatst op 2,85 en 23,25 .

Waarnemingen met waarden van 1,1 en 23,5 kwalificeren dus beide als uitschieters in de boxplot omdat ze buiten de onder- en bovengrens vallen.

Bonus : hier is de exacte code die we hebben gebruikt om deze twee boxplots in de programmeertaal R te maken:

 library (ggplot2)

#make this example reproducible 
set. seeds (2)

#create data frame
df <- data. frame (Team = factor(rep(c("A", "B"), each = 200)), 
                 Points = c(rnorm(200, mean = 15, sd = 3), 
                           rnorm(200, mean = 12, sd = 4))) 

#create box plots
ggplot(df, aes(x = Team, y = Points)) +
  stat_boxplot(geom = " errorbar ", width = 0.5) +  
  geom_boxplot() 

#calculate summary statistics for each team
tapply(df$Points, df$Team, summary)

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over boxplots:

Boxplots vergelijken
Hoe asymmetrie in boxplots te identificeren
Hoe het interkwartielbereik van een boxplot te vinden