Hoe de root mean square error (rmse) te interpreteren

Regressieanalyse is een techniek die we kunnen gebruiken om de relatie tussen een of meer voorspellende variabelen en eenresponsvariabele te begrijpen.

Een manier om te evalueren hoe goed een regressiemodel bij een dataset past, is door de gemiddelde kwadratische fout te berekenen, een metriek die ons de gemiddelde afstand vertelt tussen de voorspelde waarden van het model en de werkelijke waarden van de dataset.

Hoe lager de RMSE, hoe beter een bepaald model in een dataset kan ‘passen’.

De formule voor het vinden van de gemiddelde kwadratische fout, vaak afgekort als RMSE , is:

RMSE = √ Σ(P _ik – O _ik ) ² / n

Goud:

• Σ is een mooi symbool dat ‘som’ betekent
• _Pi is de voorspelde waarde voor de ^i- de waarneming in de dataset
• O _i is de waargenomen waarde voor de ^i- de waarneming in de dataset
• n is de steekproefomvang

In het volgende voorbeeld ziet u hoe u de RMSE voor een bepaald regressiemodel interpreteert.

Voorbeeld: Hoe RMSE te interpreteren voor een regressiemodel

Stel dat we een regressiemodel willen bouwen dat ‚gestudeerde uren‘ gebruikt om het ‚examencijfer‘ van studenten voor een bepaald toelatingsexamen voor een universiteit te voorspellen.

Van 15 studenten verzamelen wij de volgende gegevens:

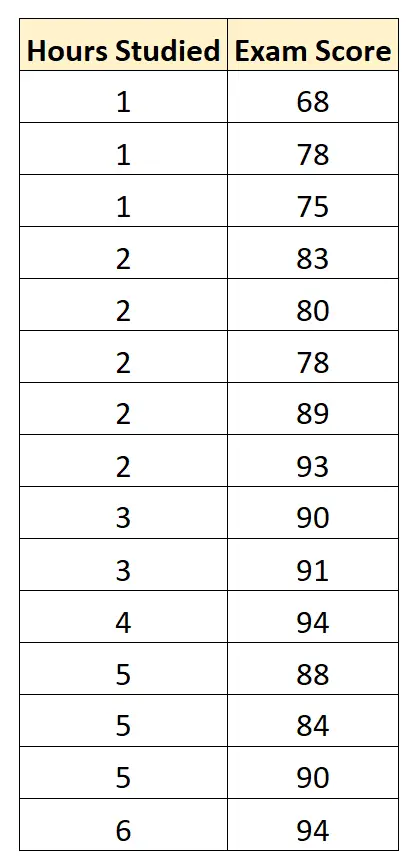
Vervolgens gebruiken we statistische software (zoals Excel, SPSS, R, Python), enz. om het volgende passende regressiemodel te vinden:

Examenscore = 75,95 + 3,08* (uren gestudeerd)

We kunnen deze vergelijking vervolgens gebruiken om de examenscore van elke student te voorspellen, op basis van het aantal uren dat hij of zij heeft gestudeerd:

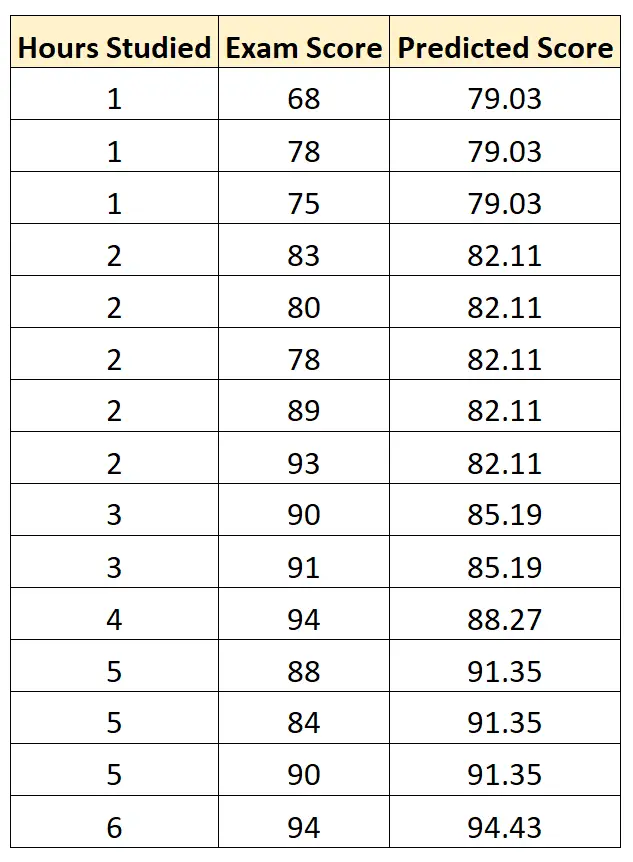
Vervolgens kunnen we het kwadratische verschil berekenen tussen elke voorspelde examenscore en de werkelijke examenscore. We kunnen dan de wortel nemen van het gemiddelde van deze verschillen:

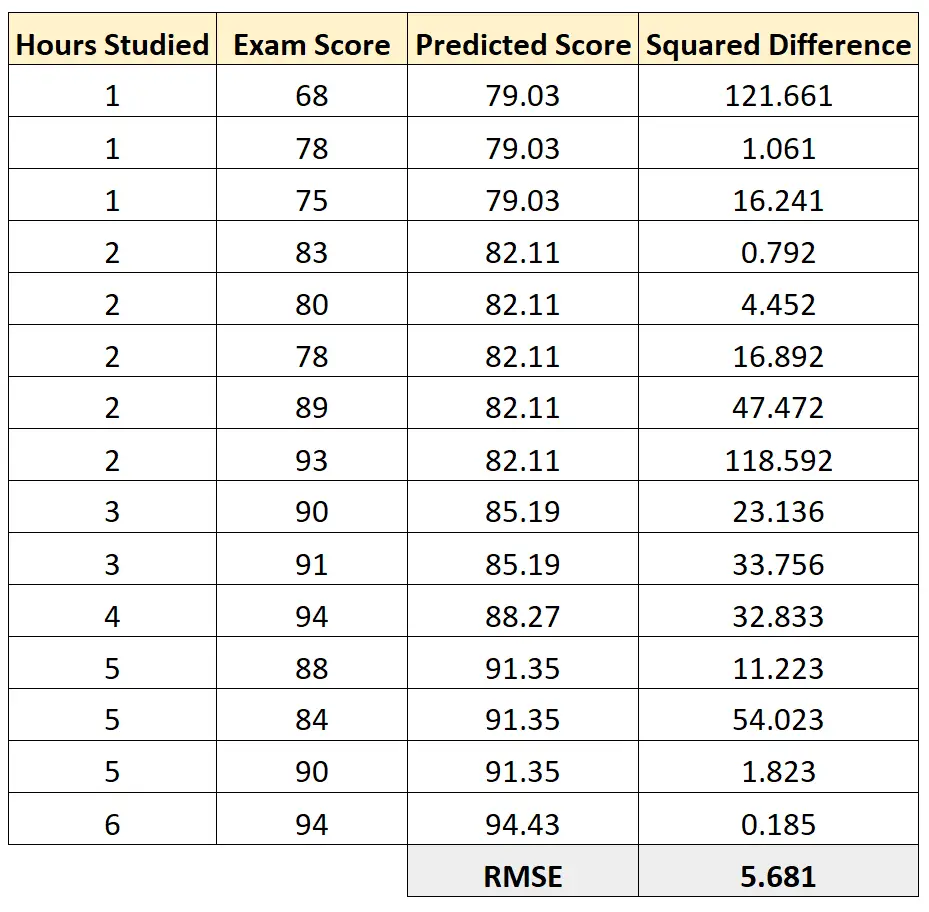
De RMSE van dit regressiemodel blijkt 5,681 te zijn.

Bedenk dat de residuen van een regressiemodel de verschillen zijn tussen de waargenomen gegevenswaarden en de voorspelde waarden van het model.

Residueel = (P _ik – O _ik )

Goud

• _Pi is de voorspelde waarde voor de ^i- de waarneming in de dataset
• O _i is de waargenomen waarde voor de ^i- de waarneming in de dataset

En onthoud dat de RMSE van een regressiemodel als volgt wordt berekend:

RMSE = √ Σ(P _ik – O _ik ) ² / n

Dit betekent dat de RMSE de vierkantswortel vertegenwoordigt van de variantie van de residuen.

Dit is een nuttige waarde om te weten, omdat het ons een idee geeft van de gemiddelde afstand tussen waargenomen datawaarden en voorspelde datawaarden.

Dit staat in contrast met de R-kwadraat van het model, die ons vertelt hoeveel van de variantie in de responsvariabele kan worden verklaard door de voorspellende variabele(n) van het model.

Vergelijking van RMSE-waarden van verschillende modellen

De RMSE is vooral nuttig voor het vergelijken van de fit van verschillende regressiemodellen.

Stel dat we bijvoorbeeld een regressiemodel willen bouwen om de examenscores van studenten te voorspellen en dat we uit verschillende potentiële modellen het best mogelijke model willen vinden.

Stel dat we drie verschillende regressiemodellen passen en de bijbehorende RMSE-waarden vinden:

• RMSE van model 1: 14,5
• RMSE van model 2: 16,7
• RMSE van model 3: 9,8

Model 3 heeft de laagste RMSE, wat ons vertelt dat het de dataset het beste onder de drie potentiële modellen kan passen.

Aanvullende bronnen

RMSE-calculator
Hoe RMSE in Excel te berekenen
Hoe RMSE in R te berekenen
Hoe RMSE in Python te berekenen