Hoe u handmatig een p-waarde uit een t-test kunt berekenen

Een van de meest gebruikte tests in de statistiek is de t-test , die vaak wordt gebruikt om te bepalen of het gemiddelde van een populatie gelijk is aan een bepaalde waarde.

Laten we bijvoorbeeld zeggen dat we willen weten of de gemiddelde hoogte van een bepaalde plantensoort gelijk is aan 15 inch. Om dit te testen, kunnen we een willekeurige steekproef van twintig planten nemen , het steekproefgemiddelde en de standaarddeviatie van de steekproef bepalen en een t-test uitvoeren om te bepalen of de gemiddelde hoogte daadwerkelijk 45 cm bedraagt.

De nul- en alternatieve hypothesen van de test zijn als volgt:

H ₀ : µ = 15

_Ha : µ ≠ 15

De formule voor de teststatistiek is:

t = ( X -μ) / (s/ √n )

waarbij x het steekproefgemiddelde is, μ het hypothetische gemiddelde is (in ons voorbeeld zou dit 15 zijn), s de standaarddeviatie van de steekproef is en n de steekproefomvang is.

Zodra we de waarde van t kennen, kunnen we statistische software of een online rekenmachine gebruiken om de overeenkomstige p-waarde te vinden. Als de p-waarde onder een bepaald alfaniveau ligt (veel voorkomende keuzes zijn 0,01, 0,05 en 0,10), dan kunnen we de nulhypothese verwerpen en concluderen dat de gemiddelde planthoogte op 15 inch niet gelijk is .

Het is echter ook mogelijk om de p-waarde van de test handmatig te schatten met behulp van een t-verdelingstabel . In dit artikel leggen wij uit hoe je dit doet.

Voorbeeld: handmatige berekening van de p-waarde uit een t-toets

Probleem : Bob wil weten of de gemiddelde hoogte van een bepaalde plantensoort gelijk is aan 45 centimeter. Om dit te testen, verzamelt hij een willekeurig monster van twintig planten en ontdekt dat het steekproefgemiddelde 14 inch is en de standaarddeviatie van het monster 3 inch. Voer een t-test uit met een alfaniveau van 0,05 om te bepalen of de werkelijke gemiddelde populatielengte feitelijk 15 inch is.

Oplossing:

Stap 1: Formuleer de nul- en alternatieve hypothesen.

H ₀ : µ = 15

_Ha : µ ≠ 15

Stap 2: Zoek de teststatistiek.

t = ( x -μ) / (s/ √n ) = (14-15) / (3/ √20 ) = -1,49

Stap 3: Zoek de p-waarde voor de teststatistiek.

Om de p-waarde handmatig te vinden, moeten we de t-verdelingstabel gebruiken met n-1 vrijheidsgraden. In ons voorbeeld is onze steekproefomvang n = 20, dus n-1 = 19.

In de onderstaande t-verdelingstabel moeten we naar de rij kijken die overeenkomt met „19“ aan de linkerkant en proberen de absolute waarde van onze teststatistiek 1.49 te vinden.

Merk op dat 1.49 niet in de tabel voorkomt, maar tussen de twee waarden 1.328 en 1.729 valt.

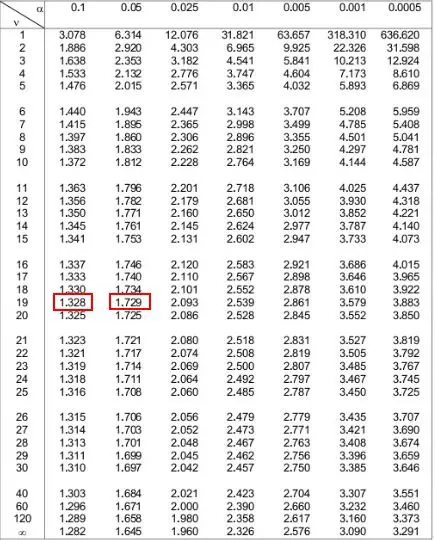
Vervolgens kunnen we kijken naar de twee alfaniveaus bovenaan de tabel die overeenkomen met deze twee getallen. We zien dat ze 0,1 en 0,05 zijn.

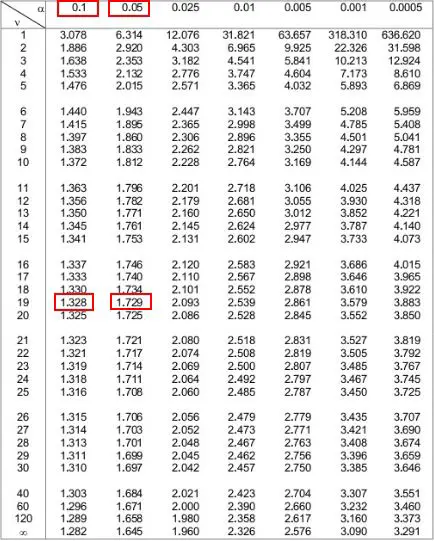
Dit betekent dat de p-waarde voor een eenzijdige toets tussen 0,1 en 0,05 ligt. Laten we het .075 noemen. Omdat onze t-toets tweezijdig is, moeten we deze waarde met 2 vermenigvuldigen. Onze geschatte p-waarde is dus 0,075 * 2 = 0,15 .

Stap 4: Trek een conclusie.

Omdat deze p-waarde niet lager is dan het gekozen alfaniveau van 0,05, kunnen we de nulhypothese niet verwerpen. We hebben dus niet genoeg bewijs om te zeggen dat de werkelijke gemiddelde hoogte van deze plantensoort iets anders is dan 15 inch.

Controleer de resultaten met een rekenmachine

We kunnen onze t -teststatistiek en vrijheidsgraden in een online p-waardecalculator pluggen om te zien hoe dicht onze geschatte p-waarde bij de werkelijke p-waarde lag:

De werkelijke p-waarde is 0,15264 , wat vrij dicht in de buurt ligt van onze geschatte p-waarde van 0,15 .

Conclusie

We hebben in dit artikel gezien dat het mogelijk is om de p-waarde van een t-toets handmatig te schatten met behulp van de t-verdelingstabel. In de meeste scenario’s hoeft u de p-waarde echter nooit met de hand te berekenen en kunt u statistische software zoals R en Excel of een online rekenmachine gebruiken om de exacte p-waarde van de test te vinden.

In de meeste gevallen, vooral bij rigoureuze statistische onderzoeken en experimenten, zul je een rekenmachine willen gebruiken om de exacte p-waarde van een t-toets te vinden om zo nauwkeurig mogelijk te zijn, maar het is goed om te weten dat je de waarde altijd handmatig kunt schatten. p-waarde van een t-toets als dat absoluut nodig is.