Hoe u een mann-whitney u-test uitvoert in excel

Een Mann-Whitney U-test (ook wel een Wilcoxon-rangsomtest genoemd) wordt gebruikt om de verschillen tussen twee steekproeven te vergelijken wanneer de steekproefverdeling niet normaal verdeeld is en de steekproefomvang klein is (n <30).

Het wordt beschouwd als het niet-parametrische equivalent van de t-test met twee steekproeven .

In deze tutorial wordt uitgelegd hoe u een Mann-Whitney U-test uitvoert in Excel.

Voorbeeld: Mann-Whitney U-test in Excel

Onderzoekers willen weten of brandstofbehandeling een verandering in het gemiddelde mpg van een auto veroorzaakt. Om dit te testen voeren ze een experiment uit waarbij ze het mpg meten van 12 auto’s met brandstofbehandeling en 12 auto’s zonder behandeling.

Omdat de steekproefomvang klein is en ze vermoeden dat de steekproefverdeling niet normaal verdeeld is, besloten ze een Mann-Whitney U-test uit te voeren om te bepalen of er een statistisch significant verschil in mpg tussen de twee groepen bestaat.

Voer de volgende stappen uit om een Mann-Whitney U-test in Excel uit te voeren.

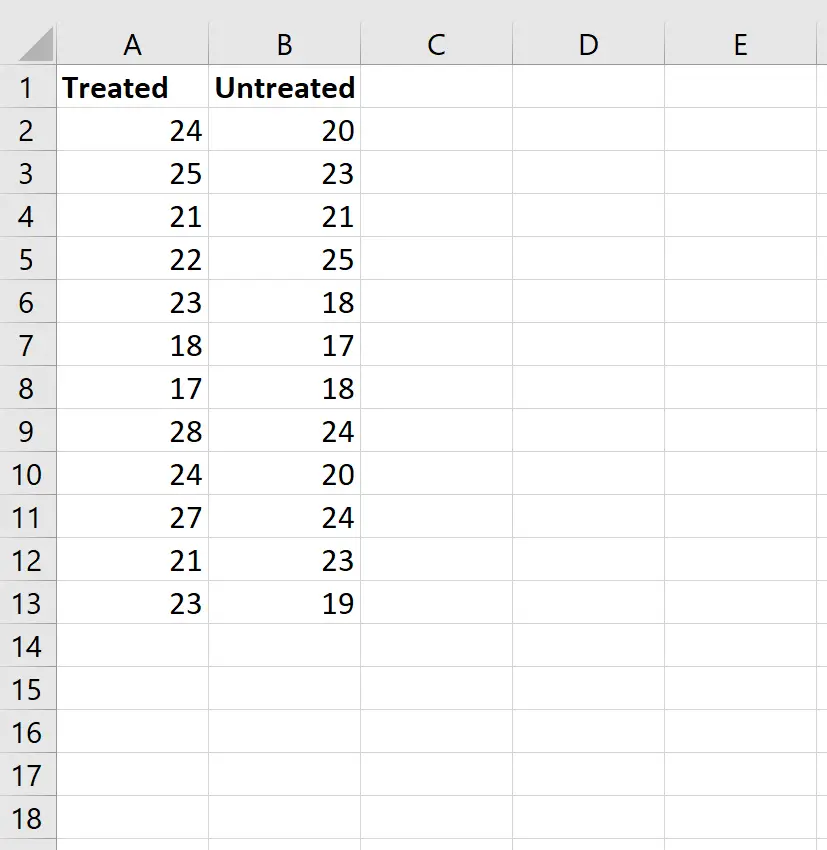
Stap 1: Voer de gegevens in.

Voer de gegevens als volgt in:

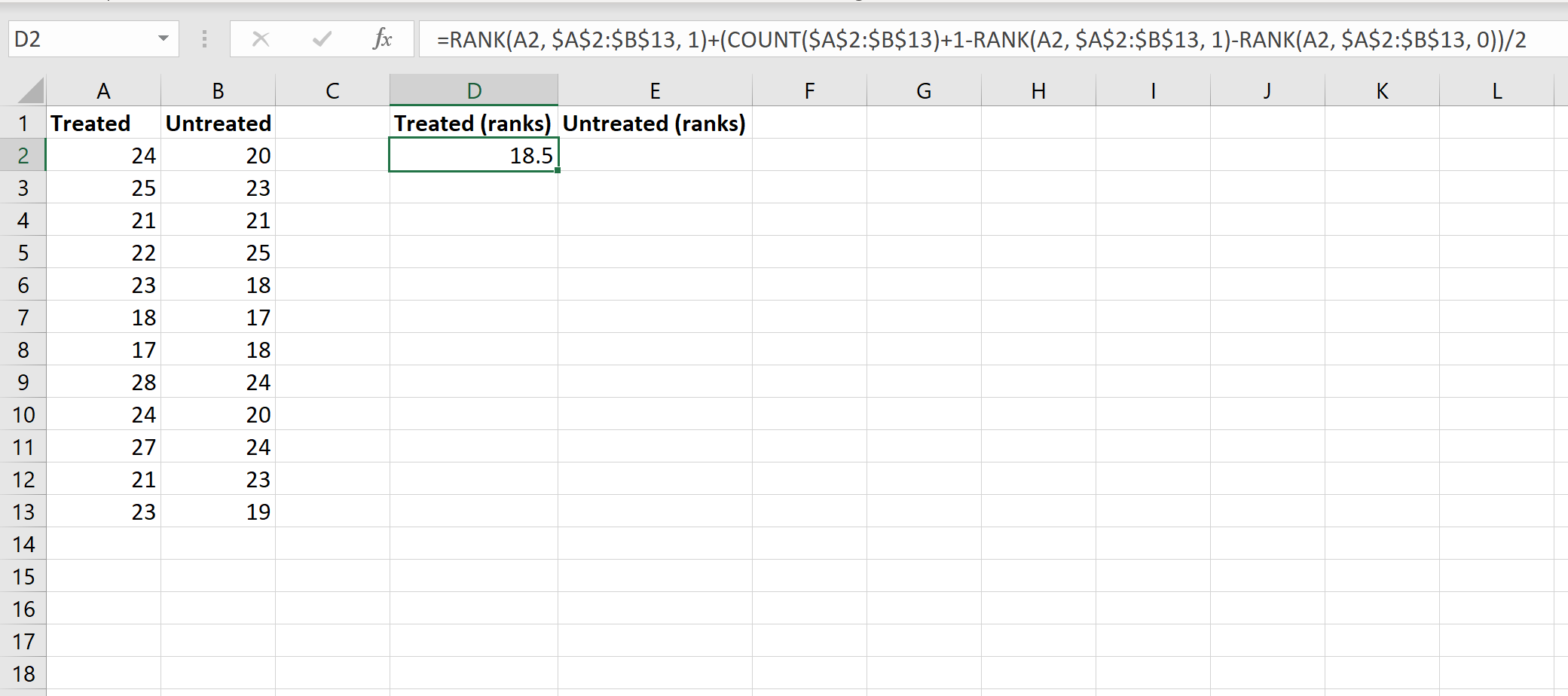
Stap 2: Bereken de ranglijst voor beide groepen.

Vervolgens berekenen we de ranglijst voor elke groep. De volgende afbeelding toont de formule die moet worden gebruikt om de rangorde van de eerste waarde in de groep Verwerkt te berekenen:

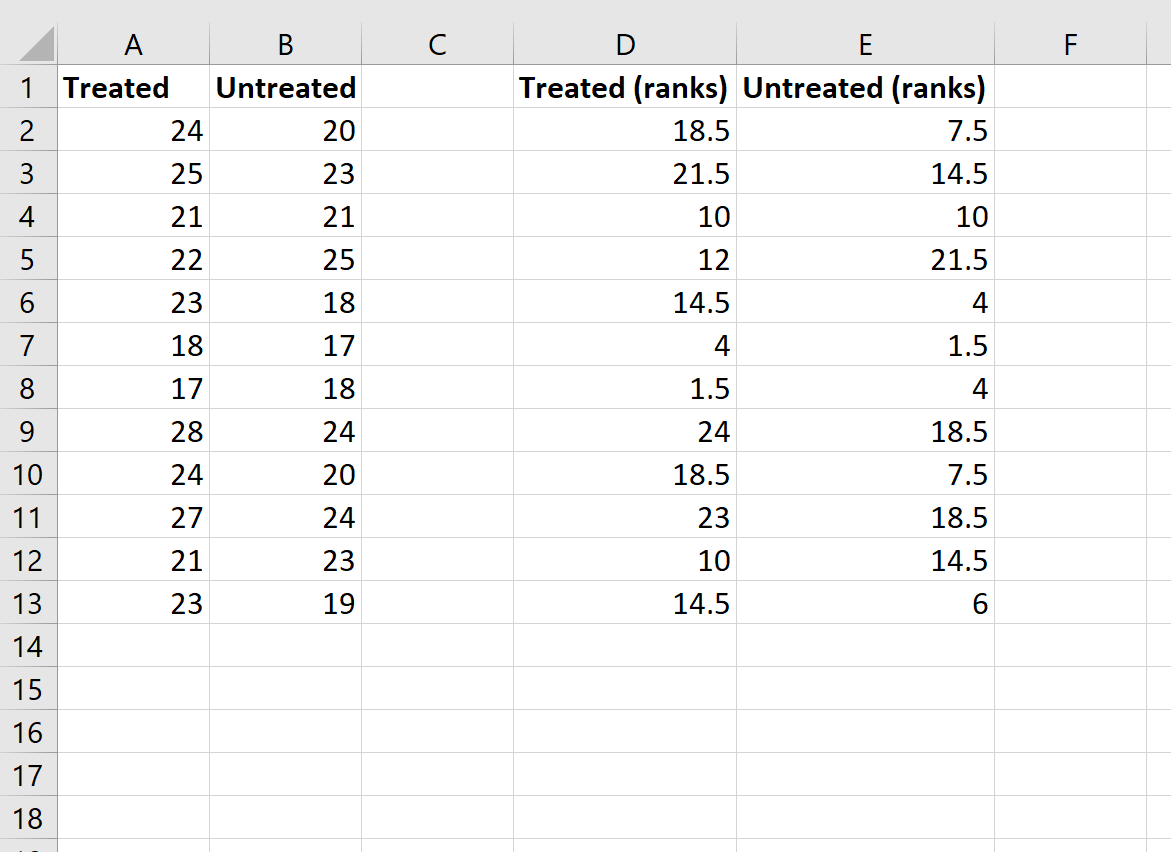
Hoewel deze formule behoorlijk ingewikkeld is, hoeft u deze maar één keer in te voeren. Vervolgens kunt u de formule eenvoudig naar alle andere cellen slepen om de rijen te vullen:

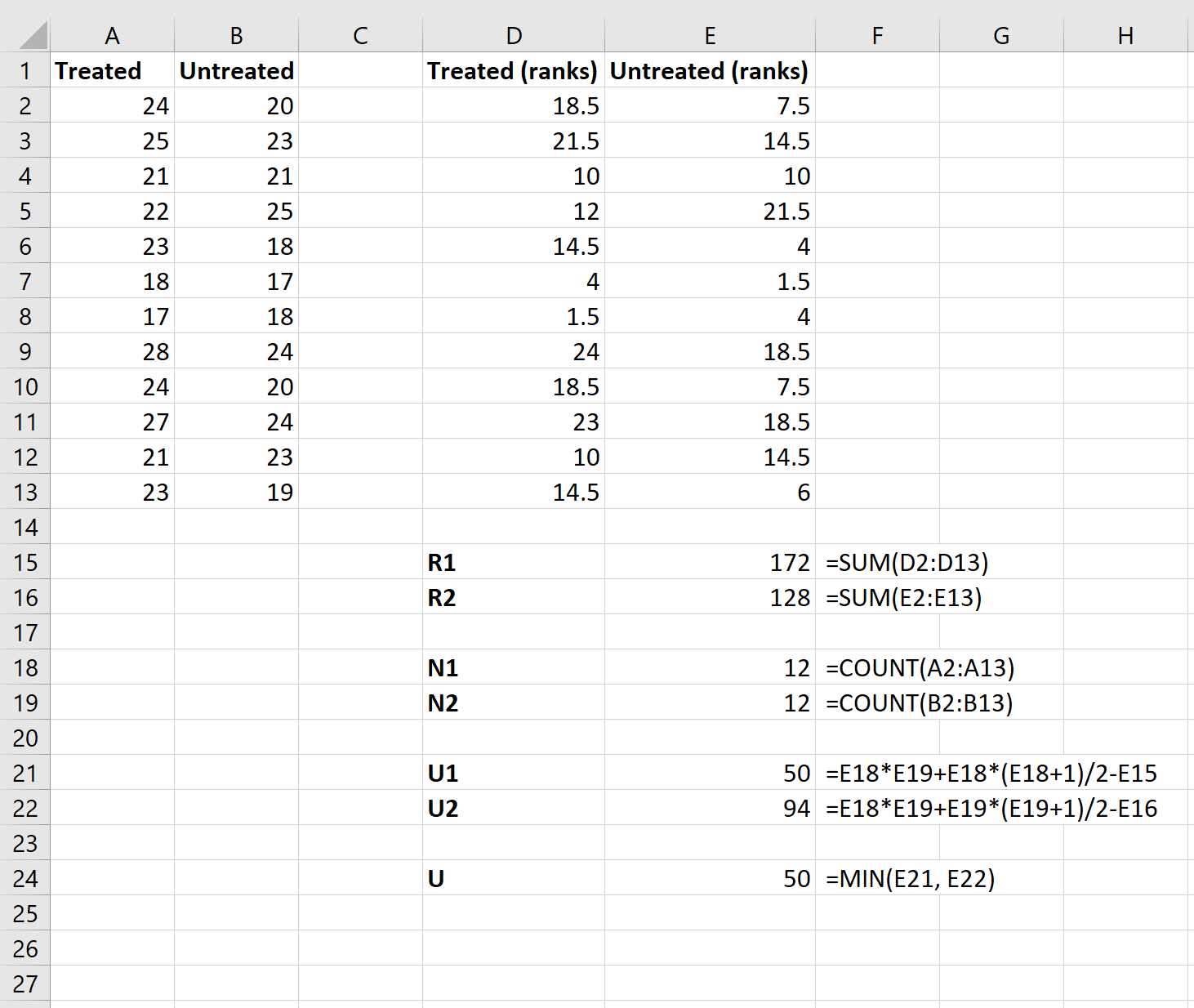
Stap 3: Bereken de waarden die nodig zijn voor de teststatistiek.

Vervolgens zullen we de volgende formules gebruiken om de som van de rangschikkingen voor elke groep, de steekproefomvang voor elke groep, de U-teststatistiek voor elke groep en de algehele U-teststatistiek te berekenen:

Stap 4: Bereken de z-teststatistiek en de bijbehorende p-waarde.

Ten slotte zullen we de volgende formules gebruiken om de z-teststatistiek en de bijbehorende p-waarde te berekenen om te bepalen of we de nulhypothese al dan niet moeten verwerpen:

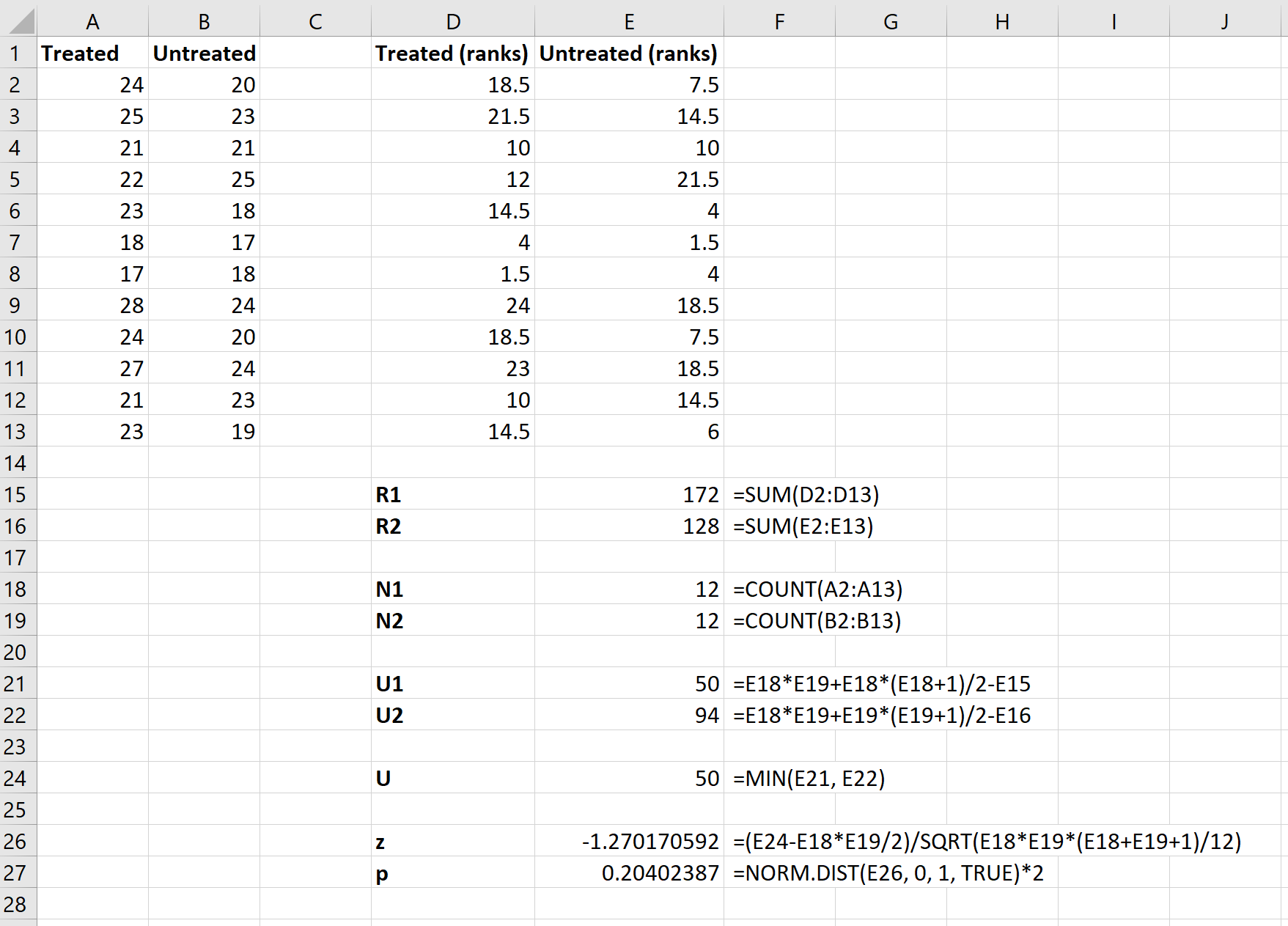
De nulhypothese van de test stelt dat beide groepen dezelfde gemiddelde mpg hebben. Omdat de p-waarde van de test ( 0,20402387 ) niet lager is dan ons significantieniveau van 0,05, slagen we er niet in de nulhypothese te verwerpen.

We hebben niet genoeg bewijs om te zeggen dat het werkelijke gemiddelde mpg tussen de twee groepen verschillend is.