Hoofdcomponentenanalyse in r: stapsgewijs voorbeeld
Principal Component Analysis, vaak afgekort PCA, is een machine learning-techniek zonder toezicht die probeert de belangrijkste componenten te vinden – lineaire combinaties van de oorspronkelijke voorspellers – die een groot deel van de variatie in een dataset verklaren.
Het doel van PCA is om het grootste deel van de variabiliteit in een dataset te verklaren met minder variabelen dan de oorspronkelijke dataset.
Voor een gegeven dataset met p -variabelen zouden we de spreidingsdiagrammen van elke paarsgewijze combinatie van variabelen kunnen onderzoeken, maar het aantal spreidingsdiagrammen kan zeer snel groot worden.
Voor p- voorspellers bestaan er p(p-1)/2-puntenwolken.
Voor een dataset met p = 15 voorspellers zouden er dus 105 verschillende spreidingsdiagrammen zijn!
Gelukkig biedt PCA een manier om een laagdimensionale weergave van een dataset te vinden die zoveel mogelijk van de variatie in de gegevens vastlegt.
Als we het grootste deel van de variatie in slechts twee dimensies kunnen vastleggen, kunnen we alle waarnemingen uit de oorspronkelijke dataset op een eenvoudig spreidingsdiagram projecteren.
De manier waarop we de belangrijkste componenten vinden is als volgt:
Gegeven een dataset met p- voorspellers : _
- Zm = ΣΦ jm _ _
- Z 1 is de lineaire combinatie van voorspellers die zoveel mogelijk variantie vastlegt.
- Z 2 is de volgende lineaire combinatie van voorspellers die de meeste variantie vastlegt terwijl deze orthogonaal (dat wil zeggen niet gecorreleerd) is met Z 1 .
- Z 3 is dan de volgende lineaire combinatie van voorspellers die de meeste variantie vastlegt terwijl deze orthogonaal is ten opzichte van Z 2 .
- Enzovoort.
In de praktijk gebruiken we de volgende stappen om de lineaire combinaties van de oorspronkelijke voorspellers te berekenen:
1. Schaal elk van de variabelen zodanig dat ze een gemiddelde van 0 en een standaarddeviatie van 1 hebben.
2. Bereken de covariantiematrix voor de geschaalde variabelen.
3. Bereken de eigenwaarden van de covariantiematrix.
Met behulp van lineaire algebra kunnen we aantonen dat de eigenvector die overeenkomt met de grootste eigenwaarde de eerste hoofdcomponent is. Met andere woorden: deze specifieke combinatie van voorspellers verklaart de grootste variantie in de gegevens.
De eigenvector die overeenkomt met de op een na grootste eigenwaarde is de tweede hoofdcomponent, enzovoort.
Deze zelfstudie biedt een stapsgewijs voorbeeld van hoe u dit proces in R kunt uitvoeren.
Stap 1: Gegevens laden
We laden eerst het Tidyverse- pakket, dat verschillende handige functies bevat voor het visualiseren en manipuleren van gegevens:
library (tidyverse)
Voor dit voorbeeld gebruiken we de in R ingebouwde dataset USArrests , die het aantal arrestaties per 100.000 inwoners in elke Amerikaanse staat in 1973 bevat voor moord , mishandeling en verkrachting .
Het omvat ook het percentage van de bevolking van elke staat dat in stedelijke gebieden woont, UrbanPop .
De volgende code laat zien hoe u de eerste rijen van de gegevensset laadt en weergeeft:
#load data data ("USArrests") #view first six rows of data head(USArrests) Murder Assault UrbanPop Rape Alabama 13.2 236 58 21.2 Alaska 10.0 263 48 44.5 Arizona 8.1 294 80 31.0 Arkansas 8.8 190 50 19.5 California 9.0 276 91 40.6 Colorado 7.9 204 78 38.7
Stap 2: Bereken de belangrijkste componenten
Na het laden van de gegevens kunnen we de ingebouwde functie pcomp() van R gebruiken om de belangrijkste componenten van de gegevensset te berekenen.
Zorg ervoor dat u scale = TRUE specificeert, zodat elk van de variabelen in de gegevensset wordt geschaald zodat het een gemiddelde van 0 en een standaarddeviatie van 1 heeft voordat u de hoofdcomponenten berekent.
Merk ook op dat de eigenvectoren in R standaard in de negatieve richting wijzen, dus we zullen vermenigvuldigen met -1 om de tekens om te keren.
#calculate main components results <- prcomp(USArrests, scale = TRUE ) #reverse the signs results$rotation <- -1*results$rotation #display main components results$rotation PC1 PC2 PC3 PC4 Murder 0.5358995 -0.4181809 0.3412327 -0.64922780 Assault 0.5831836 -0.1879856 0.2681484 0.74340748 UrbanPop 0.2781909 0.8728062 0.3780158 -0.13387773 Rape 0.5434321 0.1673186 -0.8177779 -0.08902432
We kunnen zien dat de eerste hoofdcomponent (PC1) hoge waarden heeft voor moord, mishandeling en verkrachting, wat aangeeft dat deze hoofdcomponent de grootste variatie in deze variabelen beschrijft.
We kunnen ook zien dat de tweede hoofdcomponent (PC2) een hoge waarde heeft voor UrbanPop, wat aangeeft dat deze hoofdcomponent de stedelijke bevolking benadrukt.
Houd er rekening mee dat de hoofdcomponentscores voor elke status worden opgeslagen in results$x . We zullen deze scores ook met -1 vermenigvuldigen om de tekens om te keren:
#reverse the signs of the scores results$x <- -1*results$x #display the first six scores head(results$x) PC1 PC2 PC3 PC4 Alabama 0.9756604 -1.1220012 0.43980366 -0.154696581 Alaska 1.9305379 -1.0624269 -2.01950027 0.434175454 Arizona 1.7454429 0.7384595 -0.05423025 0.826264240 Arkansas -0.1399989 -1.1085423 -0.11342217 0.180973554 California 2.4986128 1.5274267 -0.59254100 0.338559240 Colorado 1.4993407 0.9776297 -1.08400162 -0.001450164
Stap 3: Visualiseer de resultaten met een biplot
Vervolgens kunnen we een biplot maken – een plot die elk van de waarnemingen in de dataset projecteert op een spreidingsdiagram dat de eerste en tweede hoofdcomponent als assen gebruikt:
Merk op dat schaal = 0 ervoor zorgt dat de pijlen in de grafiek worden geschaald om de belastingen weer te geven.
biplot(results, scale = 0 )
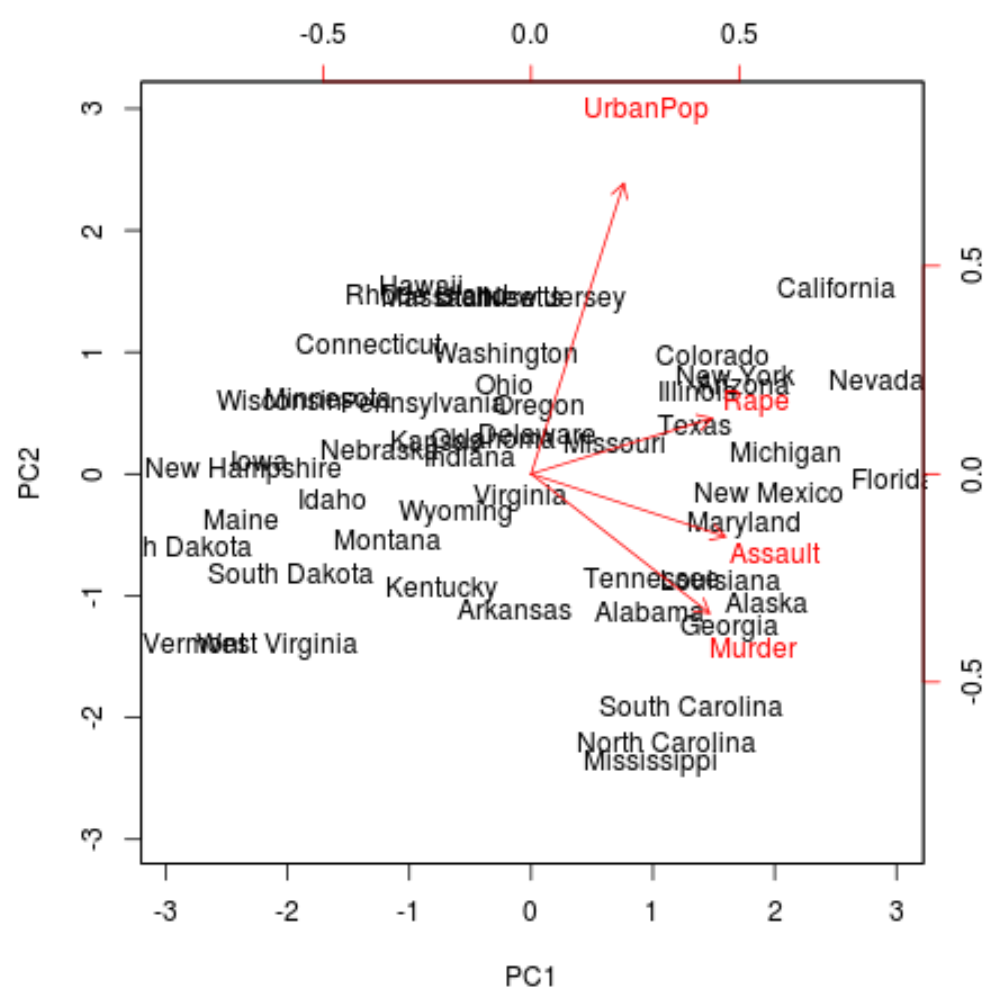
Vanuit de plot kunnen we elk van de 50 toestanden zien weergegeven in een eenvoudige tweedimensionale ruimte.
Staten die in de grafiek dicht bij elkaar liggen, hebben vergelijkbare gegevenspatronen met betrekking tot de variabelen in de oorspronkelijke gegevensset.
We kunnen ook zien dat sommige staten sterker betrokken zijn bij bepaalde misdaden dan andere. Georgië is bijvoorbeeld de staat die het dichtst bij de moordvariabele in het plot ligt.
Als we kijken naar de staten met de hoogste moordcijfers in de oorspronkelijke dataset, kunnen we zien dat Georgië bovenaan de lijst staat:
#display states with highest murder rates in original dataset head(USArrests[ order (-USArrests$Murder),]) Murder Assault UrbanPop Rape Georgia 17.4 211 60 25.8 Mississippi 16.1 259 44 17.1 Florida 15.4 335 80 31.9 Louisiana 15.4 249 66 22.2 South Carolina 14.4 279 48 22.5 Alabama 13.2 236 58 21.2
Stap 4: Zoek de variantie die door elke hoofdcomponent wordt verklaard
We kunnen de volgende code gebruiken om de totale variantie in de originele dataset te berekenen, uitgelegd door elke hoofdcomponent:
#calculate total variance explained by each principal component results$sdev^2 / sum (results$sdev^2) [1] 0.62006039 0.24744129 0.08914080 0.04335752
Uit de resultaten kunnen we het volgende opmaken:
- De eerste hoofdcomponent verklaart 62% van de totale variantie in de dataset.
- De tweede hoofdcomponent verklaart 24,7% van de totale variantie in de dataset.
- De derde hoofdcomponent verklaart 8,9% van de totale variantie in de dataset.
- De vierde hoofdcomponent verklaart 4,3% van de totale variantie in de dataset.
De eerste twee hoofdcomponenten verklaren dus het grootste deel van de totale variantie in de gegevens.
Dit is een goed teken omdat de vorige biplot elk van de waarnemingen uit de originele gegevens projecteerde op een spreidingsdiagram dat alleen rekening hield met de eerste twee hoofdcomponenten.
Het is dus geldig om de patronen in de biplot te onderzoeken om toestanden te identificeren die op elkaar lijken.
We kunnen ook een scree plot maken – een grafiek die de totale variantie weergeeft die door elke hoofdcomponent wordt verklaard – om de PCA-resultaten te visualiseren:
#calculate total variance explained by each principal component var_explained = results$sdev^2 / sum (results$sdev^2) #create scree plot qplot(c(1:4), var_explained) + geom_line() + xlab(" Principal Component ") + ylab(" Variance Explained ") + ggtitle(" Scree Plot ") + ylim(0, 1)
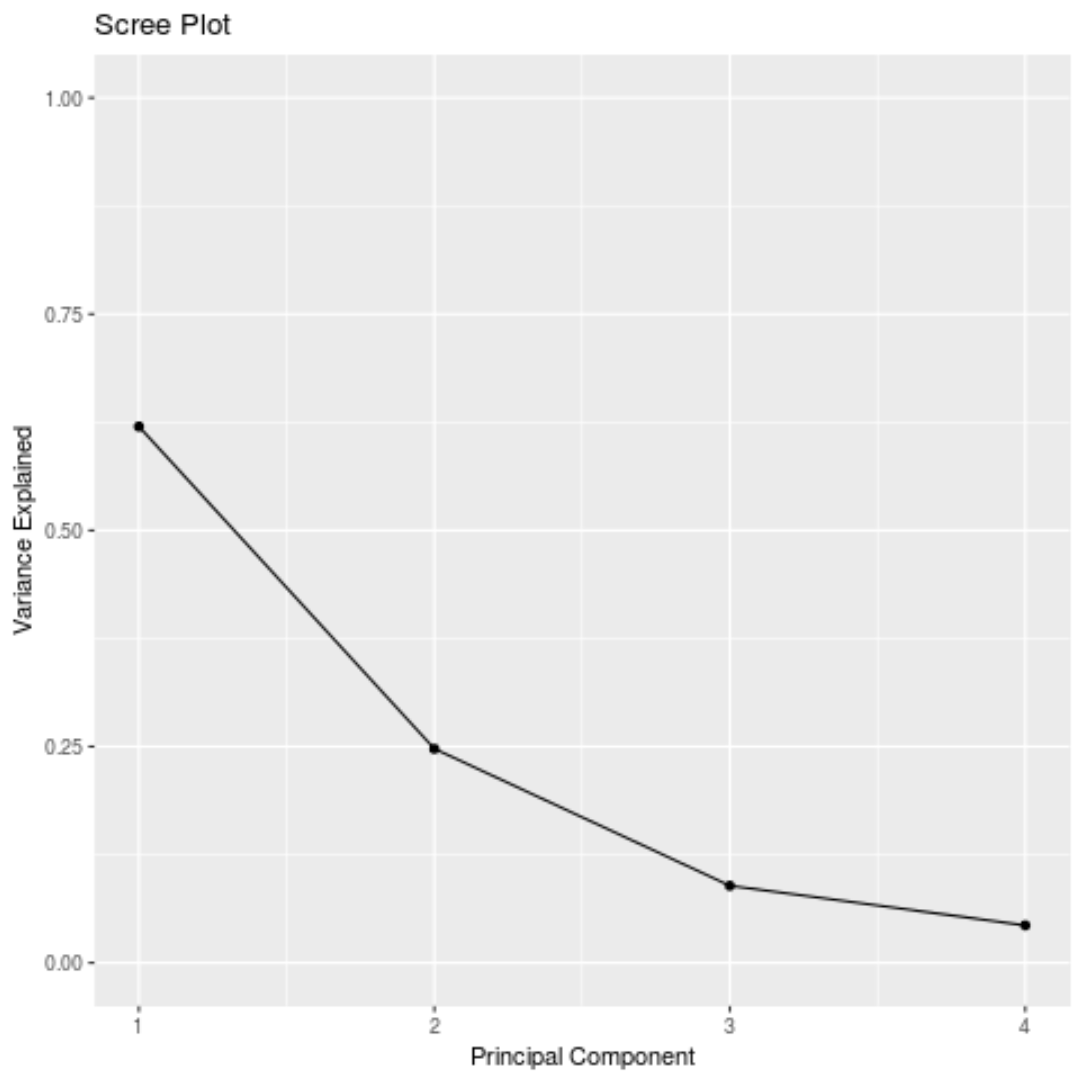
Hoofdcomponentenanalyse in de praktijk
In de praktijk wordt PCA het vaakst gebruikt om twee redenen:
1. Verkennende data-analyse – We gebruiken PCA wanneer we voor het eerst een dataset verkennen en willen begrijpen welke observaties in de data het meest op elkaar lijken.
2. Regressie van hoofdcomponenten – We kunnen PCA ook gebruiken om hoofdcomponenten te berekenen die vervolgens kunnen worden gebruikt bij regressie van hoofdcomponenten . Dit type regressie wordt vaak gebruikt als er multicollineariteit bestaat tussen de voorspellers in een dataset.
De volledige R-code die in deze tutorial wordt gebruikt, vindt u hier .