Hoofdcomponentanalyse uitvoeren in sas

Principal Component Analysis (PCA) is een machine learning-techniekzonder toezicht die tot doel heeft de belangrijkste componenten – lineaire combinaties van voorspellende variabelen – te vinden die een groot deel van de variatie in een dataset verklaren.

De eenvoudigste manier om PCA in SAS uit te voeren is door de PROC PRINCOMP -instructie te gebruiken, die de volgende basissyntaxis gebruikt:

 proc princomp data =my_data out =out_data outstat =stats;
    var var1 var2 var3;
run ;

Dit is wat elke instructie doet:

• data : de naam van de gegevensset die voor de PCA moet worden gebruikt
• out : De naam van de te maken gegevensset die alle originele gegevens bevat plus de scores van de hoofdcomponenten
• outstat : Specificeert dat er een gegevensset moet worden gemaakt met gemiddelden, standaarddeviaties, correlatiecoëfficiënten, eigenwaarden en eigenvectoren.
• var : de variabelen die moeten worden gebruikt voor PCA uit de invoergegevensset.

In het volgende stapsgewijze voorbeeld ziet u hoe u de PROC PRINCOMP- instructie in de praktijk kunt gebruiken om analyse van hoofdcomponenten in SAS uit te voeren.

Stap 1: Maak een dataset

Stel dat we de volgende dataset hebben met daarin verschillende informatie over 20 basketbalspelers:

 /*create dataset*/
data my_data;
    input points assists rebounds;
    datalines ;
22 8 4
29 7 3
10 4 12
5 5 15
35 6 2
8 3 10
10 4 8
8 4 3
2 5 17
4 5 19
9 9 4
7 6 4
31 5 3
4 6 13
5 7 8
8 8 4
10 4 8
20 4 6
25 8 8
18 8 3
;
run ;

/*view dataset*/
proc print data =my_data; 

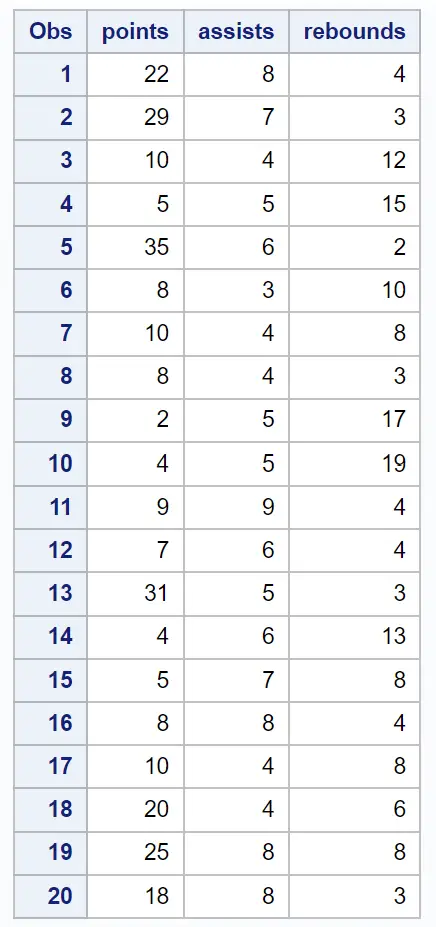
Stap 2: Voer een hoofdcomponentenanalyse uit

We kunnen de PROC PRINCOMP- instructie gebruiken om hoofdcomponentenanalyse uit te voeren met behulp van de points , assists en bounces variabelen van de dataset:

 /*perform principal components analysis*/
proc princomp data =my_data out =out_data outstat =stats;
    var points assists rebounds;
run ;

Het eerste deel van de uitvoer toont verschillende beschrijvende statistieken, waaronder de gemiddelde en standaardafwijkingen van elke invoervariabele, een correlatiematrix en de waarden van de eigenwaarden en eigenvectoren:

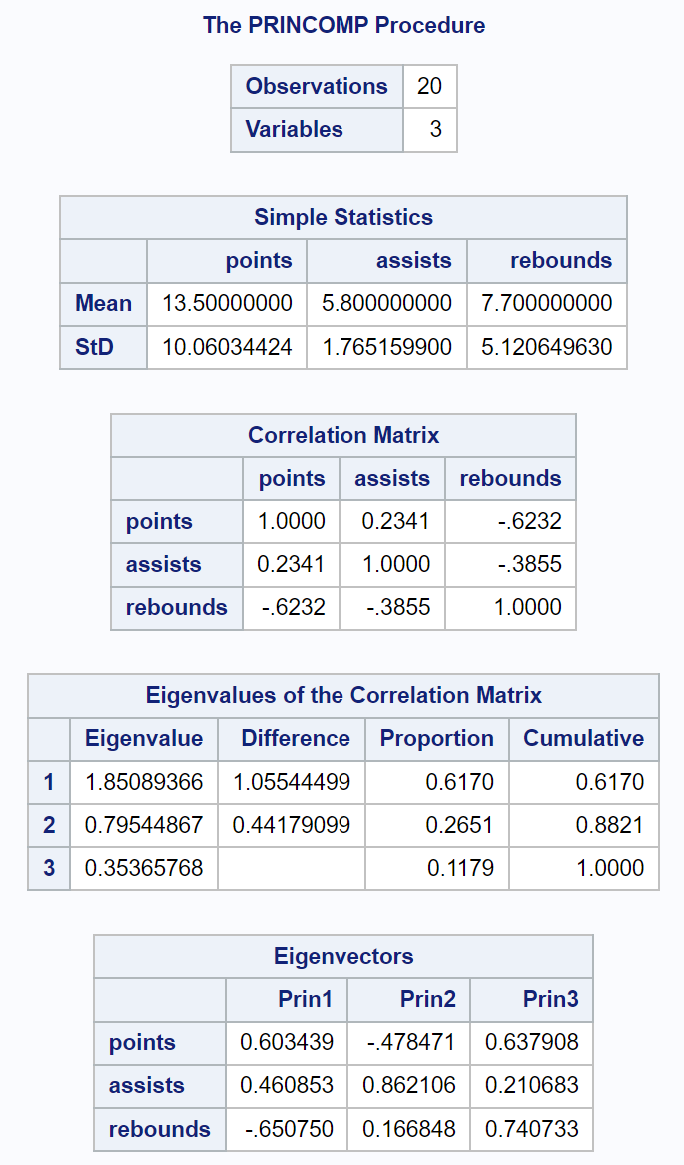
Het volgende deel van de uitvoer toont een screeplot en een verklaarde variantiegrafiek:

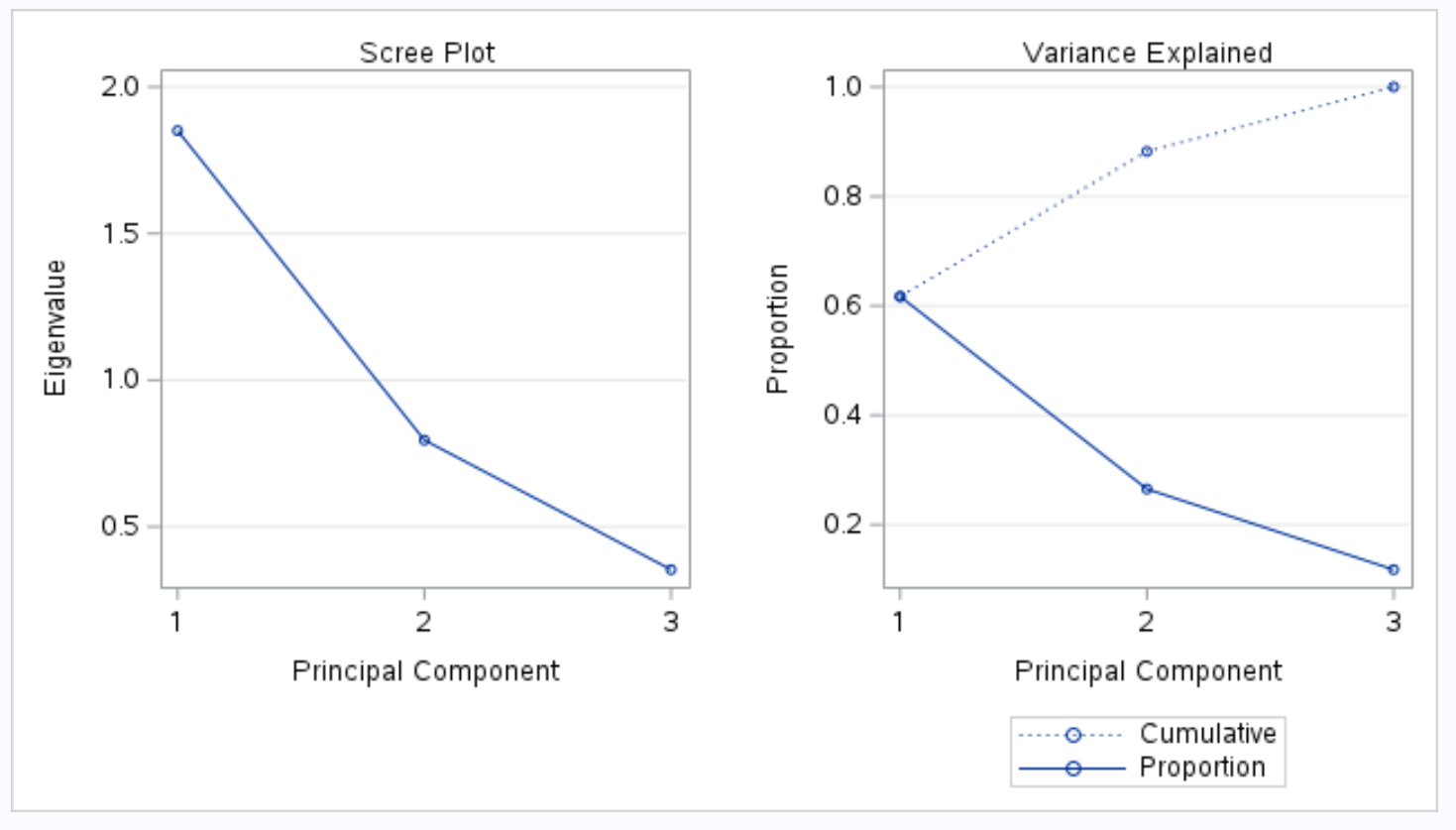
Wanneer we PCA uitvoeren, willen we vaak begrijpen welk percentage van de totale variatie in de dataset kan worden verklaard door elke hoofdcomponent.

De resulterende tabel met de titel Correlatiematrix Eigenwaarden stelt ons in staat precies te zien welk percentage van de totale variatie wordt verklaard door elke hoofdcomponent:

• De eerste hoofdcomponent verklaart 61,7% van de totale variatie in de dataset.
• De tweede hoofdcomponent verklaart 26,51% van de totale variatie in de dataset.
• De derde hoofdcomponent verklaart 11,79% van de totale variatie in de dataset.

Houd er rekening mee dat alle percentages optellen tot 100%.

De plot met de titel Variance Explored stelt ons vervolgens in staat deze waarden te visualiseren.

Op de x-as wordt de hoofdcomponent weergegeven en op de y-as het percentage van de totale variantie dat door elke afzonderlijke hoofdcomponent wordt verklaard.

Stap 3: Maak een biplot om de resultaten te visualiseren

Om de resultaten van PCA voor een bepaalde dataset te visualiseren, kunnen we een biplot maken. Dit is een plot die elke waarneming in een dataset weergeeft op een vlak dat wordt gevormd door de eerste twee hoofdcomponenten.

We kunnen de volgende syntaxis in SAS gebruiken om een biplot te maken:

 /*create dataset with column called obs to represent row numbers of original data*/
data biplot_data;
   set out_data;
   obs=_n_;
run ;

/*create biplot using values from first two principal components*/
proc sgplot data =biplot_data;
    scatter x =Prin1 y =Prin2 / datalabel =obs;
run ; 

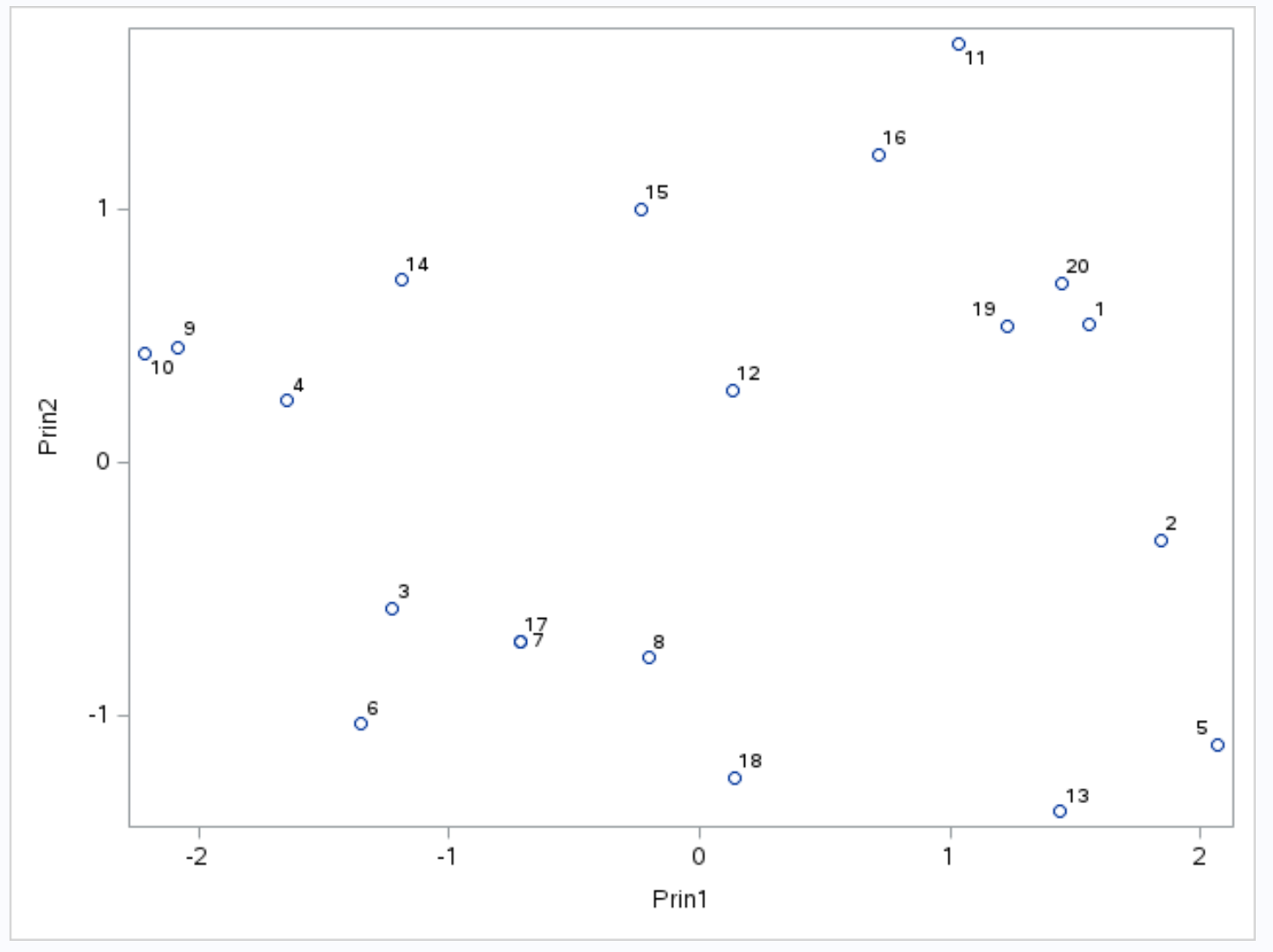
Op de x-as wordt de eerste hoofdcomponent weergegeven, op de y-as de tweede hoofdcomponent, en individuele waarnemingen uit de dataset worden in de grafiek weergegeven als kleine cirkels.

De waarnemingen die naast elkaar in de grafiek staan, hebben vergelijkbare waarden voor de drie variabelen punten , assists en rebounds .

Helemaal links in de grafiek kunnen we bijvoorbeeld zien dat waarnemingen #9 en #10 extreem dicht bij elkaar liggen.

Als we naar de originele dataset verwijzen, kunnen we de volgende waarden voor deze waarnemingen zien:

• Observatie nr. 9 : 2 punten, 5 assists, 17 rebounds
• Observatie #10 : 4 punten, 5 assists, 19 rebounds

De waarden zijn voor elk van de drie variabelen vergelijkbaar, wat verklaart waarom deze waarnemingen op de biplot zo dicht bij elkaar liggen.

We zagen ook in de resultatentabel met de titel Correlatiematrix Eigenwaarden dat de eerste twee hoofdcomponenten 88,21% van de totale variatie in de dataset voor hun rekening nemen.

Omdat dit percentage erg hoog is, is het geldig om te analyseren welke waarnemingen in de biplot dicht bij elkaar liggen, omdat de twee belangrijkste componenten waaruit de biplot bestaat, bijna alle variatie in de dataset voor hun rekening nemen.

Aanvullende bronnen

In de volgende zelfstudies wordt uitgelegd hoe u andere veelvoorkomende taken in SAS kunt uitvoeren:

Hoe u eenvoudige lineaire regressie uitvoert in SAS
Hoe u meerdere lineaire regressie uitvoert in SAS
Hoe logistische regressie uit te voeren in SAS