Hoofdcomponentregressie in r (stap voor stap)

Gegeven een reeks p- voorspellingsvariabelen en een responsvariabele, gebruikt meervoudige lineaire regressie een methode die bekend staat als de kleinste kwadraten om de resterende som van kwadraten (RSS) te minimaliseren:

RSS = Σ(y _i – ŷ _i ) ²

Goud:

• Σ : Een Grieks symbool dat som betekent
• y _i : de werkelijke responswaarde voor de ^i-de waarneming
• ŷ _i : De voorspelde responswaarde op basis van het meervoudige lineaire regressiemodel

Wanneer voorspellende variabelen echter sterk gecorreleerd zijn, kan multicollineariteit een probleem worden. Dit kan schattingen van modelcoëfficiënten onbetrouwbaar maken en een hoge variantie vertonen.

Eén manier om dit probleem te vermijden is het gebruik van regressie van hoofdcomponenten , waarbij M lineaire combinaties (zogenaamde „hoofdcomponenten“) van de oorspronkelijke p- voorspellers worden gevonden en vervolgens de kleinste kwadraten worden gebruikt om een lineair regressiemodel te passen met behulp van de hoofdcomponenten als voorspellers.

Deze zelfstudie biedt een stapsgewijs voorbeeld van het uitvoeren van regressie van hoofdcomponenten in R.

Stap 1: Laad de benodigde pakketten

De eenvoudigste manier om regressie van hoofdcomponenten in R uit te voeren, is door functies in het pls- pakket te gebruiken.

 #install pls package (if not already installed)
install.packages(" pls ")

load pls package
library(pls)

Stap 2: Pas het PCR-model aan

Voor dit voorbeeld gebruiken we de ingebouwde R-dataset genaamd mtcars , die gegevens over verschillende soorten auto’s bevat:

 #view first six rows of mtcars dataset
head(mtcars)

                   mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3,460 20.22 1 0 3 1

Voor dit voorbeeld passen we een PCR-model (Principal Components Regressie) toe met hp als responsvariabele en de volgende variabelen als voorspellende variabelen:

• mpg
• weergave
• shit
• gewicht
• qsec

De volgende code laat zien hoe u het PCR-model aan deze gegevens kunt aanpassen. Let op de volgende argumenten:

• scale=TRUE : Dit vertelt R dat elk van de voorspellende variabelen moet worden geschaald om een gemiddelde van 0 en een standaarddeviatie van 1 te hebben. Dit zorgt ervoor dat geen enkele voorspellende variabele teveel invloed heeft in het model als deze in verschillende eenheden wordt gemeten. .
• validation=”CV” : Dit vertelt R om k-voudige kruisvalidatie te gebruiken om de modelprestaties te evalueren. Merk op dat hierbij standaard k=10 vouwen worden gebruikt. Houd er ook rekening mee dat u in plaats daarvan „LOOCV“ kunt opgeven om Leave-One-Out-kruisvalidatie uit te voeren.

 #make this example reproducible
set.seed(1)

#fit PCR model
model <- pcr(hp~mpg+disp+drat+wt+qsec, data=mtcars, scale= TRUE , validation=" CV ")

Stap 3: Kies het aantal hoofdcomponenten

Nadat we het model hebben aangepast, moeten we bepalen hoeveel hoofdcomponenten de moeite waard zijn om te behouden.

Om dit te doen, hoeft u alleen maar naar de testroot mean square error (test RMSE) te kijken, berekend door k-cross-validatie:

 #view summary of model fitting
summary(model)

Data: 
	Y dimension: 32 1
Fit method: svdpc
Number of components considered: 5

VALIDATION: RMSEP
Cross-validated using 10 random segments.
       (Intercept) 1 comp 2 comps 3 comps 4 comps 5 comps
CV 69.66 44.56 35.64 35.83 36.23 36.67
adjCV 69.66 44.44 35.27 35.43 35.80 36.20

TRAINING: % variance explained
    1 comp 2 comps 3 comps 4 comps 5 comps
X 69.83 89.35 95.88 98.96 100.00
hp 62.38 81.31 81.96 81.98 82.03

Er zijn twee interessante tabellen in het resultaat:

1. VALIDATIE: RMSEP

Deze tabel vertelt ons de RMSE-test berekend door k-voudige kruisvalidatie. We kunnen het volgende zien:

• Als we alleen de originele term in het model gebruiken, is de RMSE van de test 69.66 .
• Als we de eerste hoofdcomponent toevoegen, daalt de RMSE-test naar 44,56.
• Als we de tweede hoofdcomponent toevoegen, daalt de RMSE-test naar 35,64.

We kunnen zien dat het toevoegen van extra hoofdcomponenten feitelijk resulteert in een toename van de RMSE van de test. Het lijkt er dus op dat het optimaal zou zijn om in het uiteindelijke model slechts twee hoofdcomponenten te gebruiken.

2. TRAINING: % variantie uitgelegd

Deze tabel vertelt ons het variantiepercentage in de responsvariabele, verklaard door de hoofdcomponenten. We kunnen het volgende zien:

• Met alleen de eerste hoofdcomponent kunnen we 69,83% van de variatie in de responsvariabele verklaren.
• Door de tweede hoofdcomponent toe te voegen, kunnen we 89,35% van de variatie in de responsvariabele verklaren.

Merk op dat we nog steeds meer variantie kunnen verklaren door meer hoofdcomponenten te gebruiken, maar we kunnen zien dat het toevoegen van meer dan twee hoofdcomponenten het percentage verklaarde variantie feitelijk niet veel verhoogt.

We kunnen de RMSE-test (samen met de MSE- en R-kwadraattest) ook visualiseren als een functie van het aantal hoofdcomponenten met behulp van de validatieplot()- functie.

 #visualize cross-validation plots
validationplot(model)
validationplot(model, val.type="MSEP")
validationplot(model, val.type="R2") 

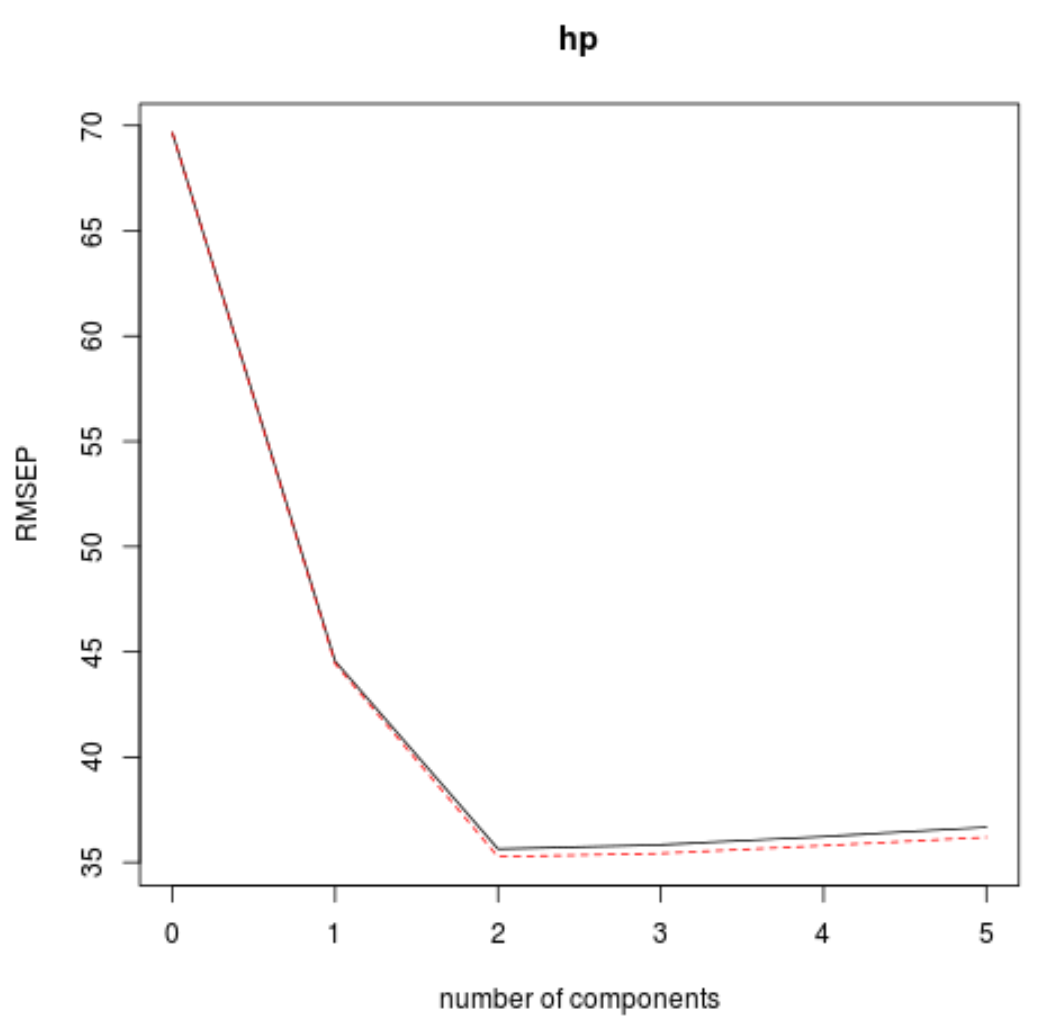
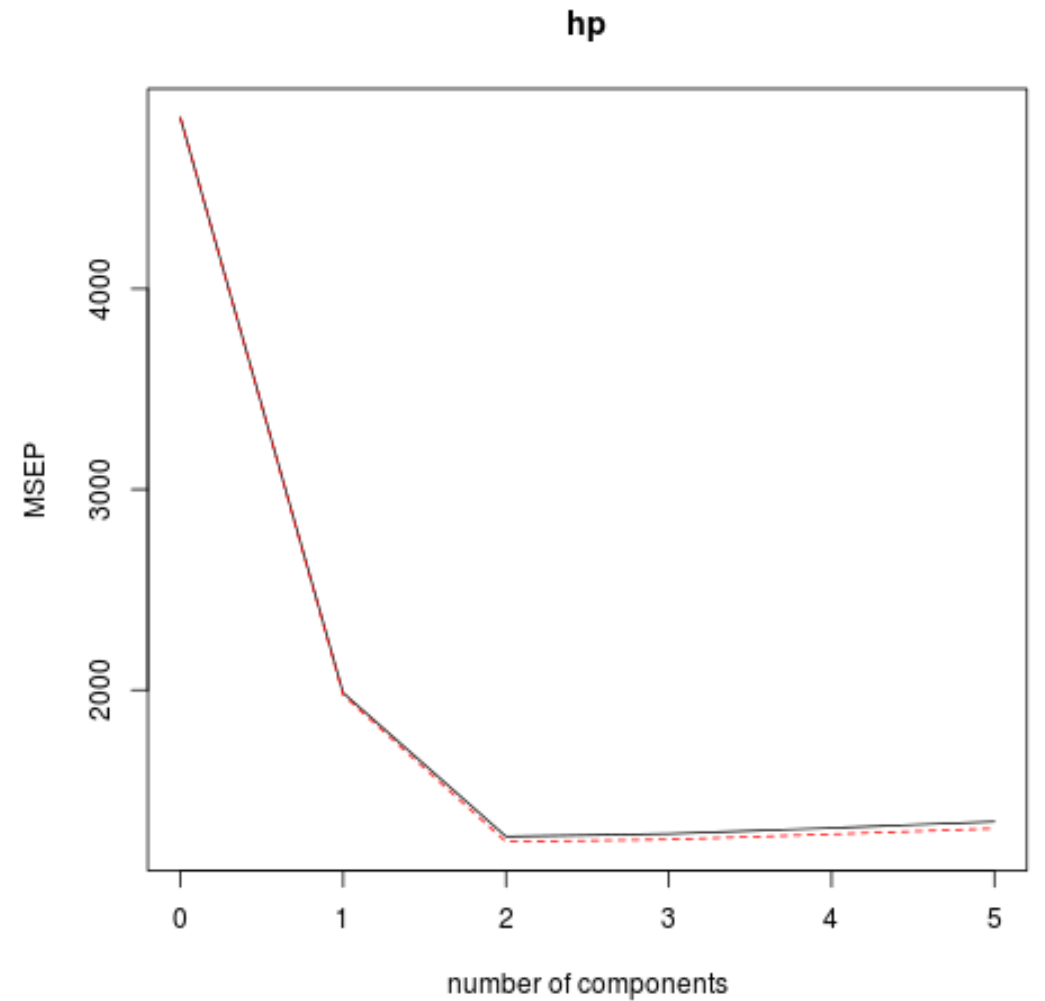
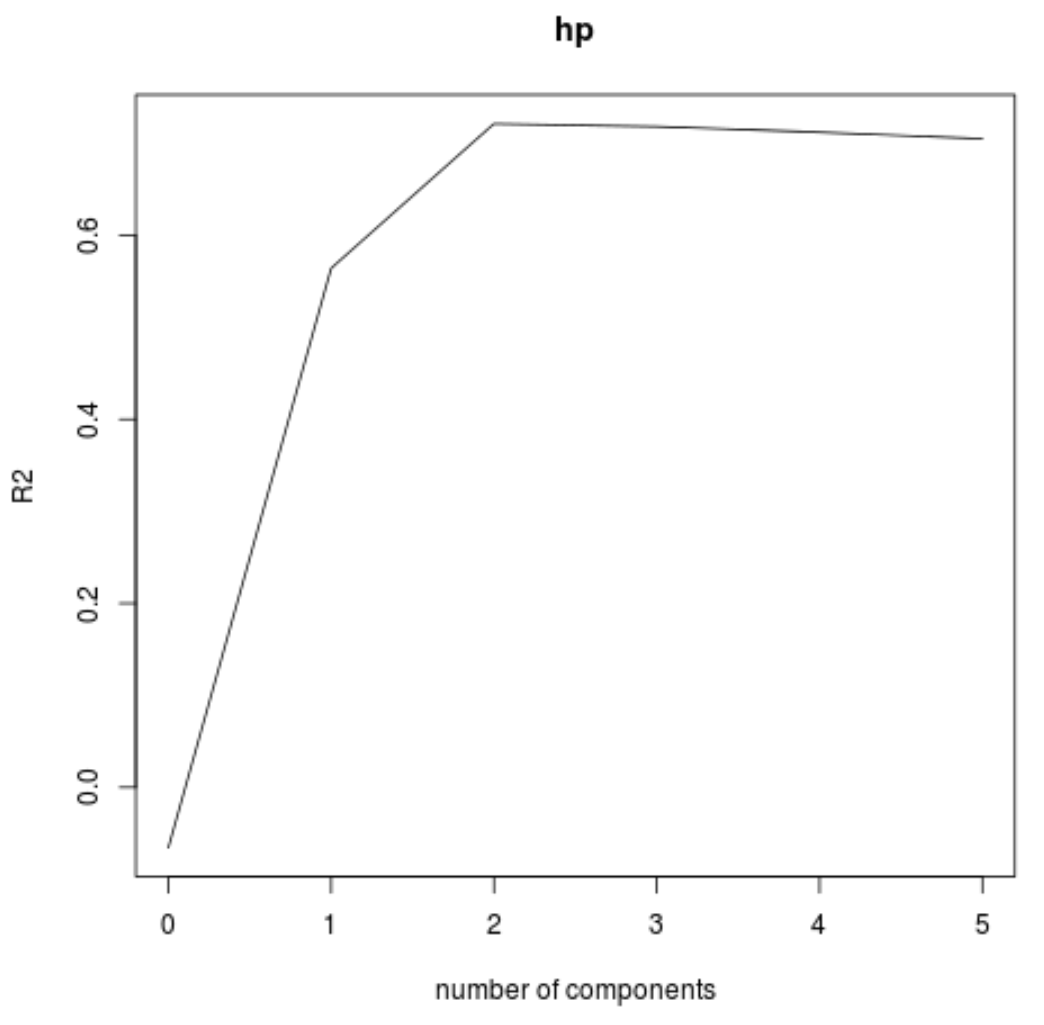
In elke grafiek kunnen we zien dat de modelfit verbetert door twee hoofdcomponenten toe te voegen, maar dat deze de neiging heeft te verslechteren als we meer hoofdcomponenten toevoegen.

Het optimale model omvat dus alleen de eerste twee hoofdcomponenten.

Stap 4: Gebruik het definitieve model om voorspellingen te doen

We kunnen het laatste PCR-model met twee hoofdcomponenten gebruiken om voorspellingen te doen over nieuwe waarnemingen.

De volgende code laat zien hoe u de oorspronkelijke gegevensset kunt opsplitsen in een trainings- en testset en hoe u het PCR-model met twee hoofdcomponenten kunt gebruiken om voorspellingen te doen over de testset.

 #define training and testing sets
train <- mtcars[1:25, c("hp", "mpg", "disp", "drat", "wt", "qsec")]
y_test <- mtcars[26: nrow (mtcars), c("hp")]
test <- mtcars[26: nrow (mtcars), c("mpg", "disp", "drat", "wt", "qsec")]
    
#use model to make predictions on a test set
model <- pcr(hp~mpg+disp+drat+wt+qsec, data=train, scale= TRUE , validation=" CV ")
pcr_pred <- predict(model, test, ncomp= 2 )

#calculate RMSE
sqrt ( mean ((pcr_pred - y_test)^2))

[1] 56.86549

We zien dat de RMSE van de test 56.86549 blijkt te zijn. Dit is de gemiddelde afwijking tussen de voorspelde pk- waarde en de waargenomen pk- waarde voor de waarnemingen van de testset.

Het volledige gebruik van de R-code in dit voorbeeld vindt u hier .