Hypergeometrische distributie

Von Dr.benjamin anderson August 6, 2023 Waarschijnlijkheid Keine Kommentare

In dit artikel leggen we uit wat de hypergeometrische verdeling is en hoe bij dit type verdeling een kans wordt berekend. U vindt online de formule voor de hypergeometrische verdeling, wat de kenmerken ervan zijn, evenals een rekenmachine om de waarschijnlijkheid van de hypergeometrische verdeling te berekenen.

Wat is de hypergeometrische verdeling?

De hypergeometrische verdeling is een waarschijnlijkheidsverdeling die het aantal succesvolle gevallen beschrijft in een willekeurige extractie zonder vervanging van n elementen uit een populatie.

Dat wil zeggen dat de hypergeometrische verdeling wordt gebruikt om de waarschijnlijkheid te berekenen van het verkrijgen van x successen bij het extraheren van n elementen uit een populatie zonder een van deze te vervangen.

De hypergeometrische verdeling heeft drie parameters:

N : is het aantal elementen in de populatie (N = 0, 1, 2,…).
K : is het maximale aantal succesgevallen (K = 0, 1, 2,…,N). Omdat bij een hypergeometrische verdeling een element alleen als een „succes“ of een „mislukking“ kan worden beschouwd, is NK het maximale aantal faalgevallen.
n : is het aantal niet-vervangingsophaalacties dat wordt uitgevoerd.

$X \sim HG(N,K,n)$

Een discrete willekeurige variabele X die een hypergeometrische verdeling heeft met parameters N=8, K=5 en n=3, wordt bijvoorbeeld als volgt gedefinieerd:

$X \sim HG(8,5,3)$

Hypergeometrische distributieformule

De formule voor de hypergeometrische verdeling is het product van het combinatorische getal van K gedeeld door x door het combinatorische getal van NK gedeeld door nx gedeeld door het combinatorische getal van N gedeeld door n .

Waarbij N de populatiegrootte is, K het totaal aantal gunstige gevallen, n het aantal extracties zonder vervanging en x het aantal gunstige gevallen waarvoor de kans van voorkomen moet worden berekend.

👉 U kunt de onderstaande rekenmachine gebruiken om de waarschijnlijkheid te berekenen van een gebeurtenis van een variabele die de hypergeometrische verdeling volgt.

Voorbeeld van hypergeometrische distributie

Nadat we de definitie en formule van hypergeometrische verdeling hebben gezien, zullen we nu stap voor stap een voorbeeld oplossen, zodat u weet hoe u de waarschijnlijkheid van een hypergeometrische verdeling kunt berekenen.

In een zak stoppen we 20 blauwe ballen en 30 rode ballen, dat wil zeggen dat er in totaal 50 ballen in de zak zitten. Als we 12 ballen trekken zonder er één te vervangen, bereken dan de kans dat we 4 blauwe ballen trekken.

Het eerste dat we moeten doen om de oefening op te lossen, is het identificeren van de parameters van de hypergeometrische verdeling. In dit geval is het totale aantal elementen in de populatie 50 ( N =50), het maximale aantal gunstige gevallen is 20 ( K =20) en worden er 12 ballen getrokken ( n =12).

$\left.\begin{array}{c}N=50\\[2ex]K=20\\[2ex]n=12\end{array}\right\} \longrightarrow \ X\sim HG(50,20,12)$

We willen de waarschijnlijkheid berekenen dat we 4 blauwe ballen trekken ( x = 4), dus passen we de hypergeometrische verdelingsformule toe, vervangen we de variabelen door hun overeenkomstige waarden en voeren we de berekening uit:

$P\bigl[X=x\bigr]=\cfrac{\begin{pmatrix}K\\x\end{pmatrix}\begin{pmatrix}N-K\\n-x\end{pmatrix}}{\begin{pmatrix}N\\n\end{pmatrix}}$

$\begin{aligned}P\bigl[X=4\bigr]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}50-20\\12-4\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}30\\8\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=0,2336 \end{aligned}$

Hypergeometrische distributiecalculator

Voer de parameters van de hypergeometrische verdeling in de volgende online calculator in om de waarschijnlijkheid van het optreden van de gewenste gebeurtenis te berekenen.

Onthoud dat N de populatiegrootte is, K het totale aantal gunstige gevallen, n de steekproefomvang is en x de waarde is waarvoor we de waarschijnlijkheid willen vinden dat dit gebeurt.

Kenmerken van de hypergeometrische distributie

De hypergeometrische verdeling heeft de volgende eigenschappen:

De verwachte waarde van een hypergeometrische verdeling is gelijk aan het aantal elementen in de steekproef vermenigvuldigd met het totale aantal gunstige gevallen gedeeld door het aantal elementen in de populatie.

$E[X]=\cfrac{n\cdot K}{N}$

De modus van een hypergeometrische verdeling is de waarde naar beneden afgerond vanaf het product van n+1 maal K+1 gedeeld door N+2 .

$\displaystyle M=\Bigg\lfloor \frac{(n+1)(K+1)}{N+2}\Bigg\rfloor$

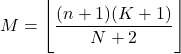
De variantie van een hypergeometrische verdeling kan worden verkregen met behulp van de volgende uitdrukking:

$\displaystyle Var[X]=\cfrac{nK}{N}\left(\frac{N-K}{N}\right)\left(\frac{N-n}{N-1}\right)$

De momentgenererende functie van een hypergeometrische verdeling is als volgt:

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K-n+1; e^{t}) } }{{N \choose n}}$

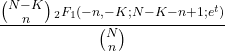
De karakteristieke functie van de hypergeometrische verdeling is als volgt:

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K - n + 1; e^{it}) }}{{N \choose n}}$

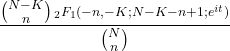
De waarschijnlijkheid van het optreden van een bepaald aantal gebeurtenissen kan worden berekend op basis van de waarschijnlijkheid van het vorige getal met behulp van de recursieve voor de hypergeometrische verdeling:

$P[X=x+1]=\cfrac{(K-x)(n-x)}{(x+1)(N-K-n+x-1)}\cdot P[X=x]$

Hypergeometrische distributie en binomiale distributie

Het verschil tussen de hypergeometrische verdeling en de binomiale verdeling is de vervanging. Hypergeometrische verdeling wordt gebruikt wanneer opzoekingen niet worden vervangen, maar bij binomiale verdelingen worden ophaalacties wel vervangen.

Als we bijvoorbeeld willekeurig vijf kaarten in een kaartspel trekken en we willen de waarschijnlijkheid berekenen dat we een bepaalde kaart krijgen, moeten we, als we niet elke kaart die we trekken vervangen, de hypergeometrische verdeling gebruiken om de berekening uit te voeren. Maar als we bij het verwijderen van een kaart deze terugleggen voordat we de volgende extractie uitvoeren, dan moeten we de binominale verdeling gebruiken om de waarschijnlijkheid te berekenen.

Wanneer het getal N groot is, de verhouding n/N klein is en het aantal gewenste gunstige gevallen zeer klein is, kunnen we de hypergeometrische verdeling gebruiken als benadering van de binomiale verdeling. Ik raad het echter niet aan omdat het resultaat niet zo betrouwbaar zal zijn en bovendien is het gemakkelijker om kansen te berekenen met de binominale wet dan met de hypergeometrische wet.

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder