Hoe hypergeometrische distributie in excel te gebruiken

Dehypergeometrische verdeling beschrijft de waarschijnlijkheid dat k objecten met een bepaald kenmerk worden gekozen in n trekkingen zonder vervanging, uit een eindige populatie van grootte N die K objecten met dit kenmerk bevat.

Als een willekeurige variabele X een hypergeometrische verdeling volgt, kan de kans op het kiezen van k objecten met een bepaald kenmerk worden gevonden met de volgende formule:

P(X=k) = _K C _k ( _NK C _nk ) / _N C _n

Goud:

• N: populatieomvang
• K: aantal objecten in de populatie met een bepaald kenmerk
• n: steekproefomvang
• k: aantal objecten in het monster met een bepaalde functionaliteit
• _K C _k : aantal combinaties van K dingen die k tegelijk worden genomen

Om de kansen te berekenen die verband houden met de hypergeometrische verdeling in Excel, kunnen we de volgende formule gebruiken:

 =HYPGEOM.DIST(sample_s, number_sample, population_s, number_pop, cumulative)

Goud:

• sample_s : aantal successen in de steekproef
• number_sample : steekproefomvang
• populatie_s : aantal successen in de populatie
• number_pop : populatiegrootte
• cumulatief : Of de cumulatieve verdelingsfunctie moet worden berekend

De volgende voorbeelden laten zien hoe u deze formule in de praktijk kunt gebruiken.

Voorbeeld 1: Kaarten kiezen uit een stapel

Er zijn 4 Koninginnen in een standaard kaartspel van 52 kaarten. Stel dat we willekeurig een kaart uit een stapel kiezen en vervolgens, zonder vervanging, willekeurig een andere kaart uit de stapel kiezen. Wat is de kans dat beide kaarten koninginnen zijn?

We kunnen de volgende formule in Excel gebruiken om de kans te berekenen dat kaarten koninginnen zijn:

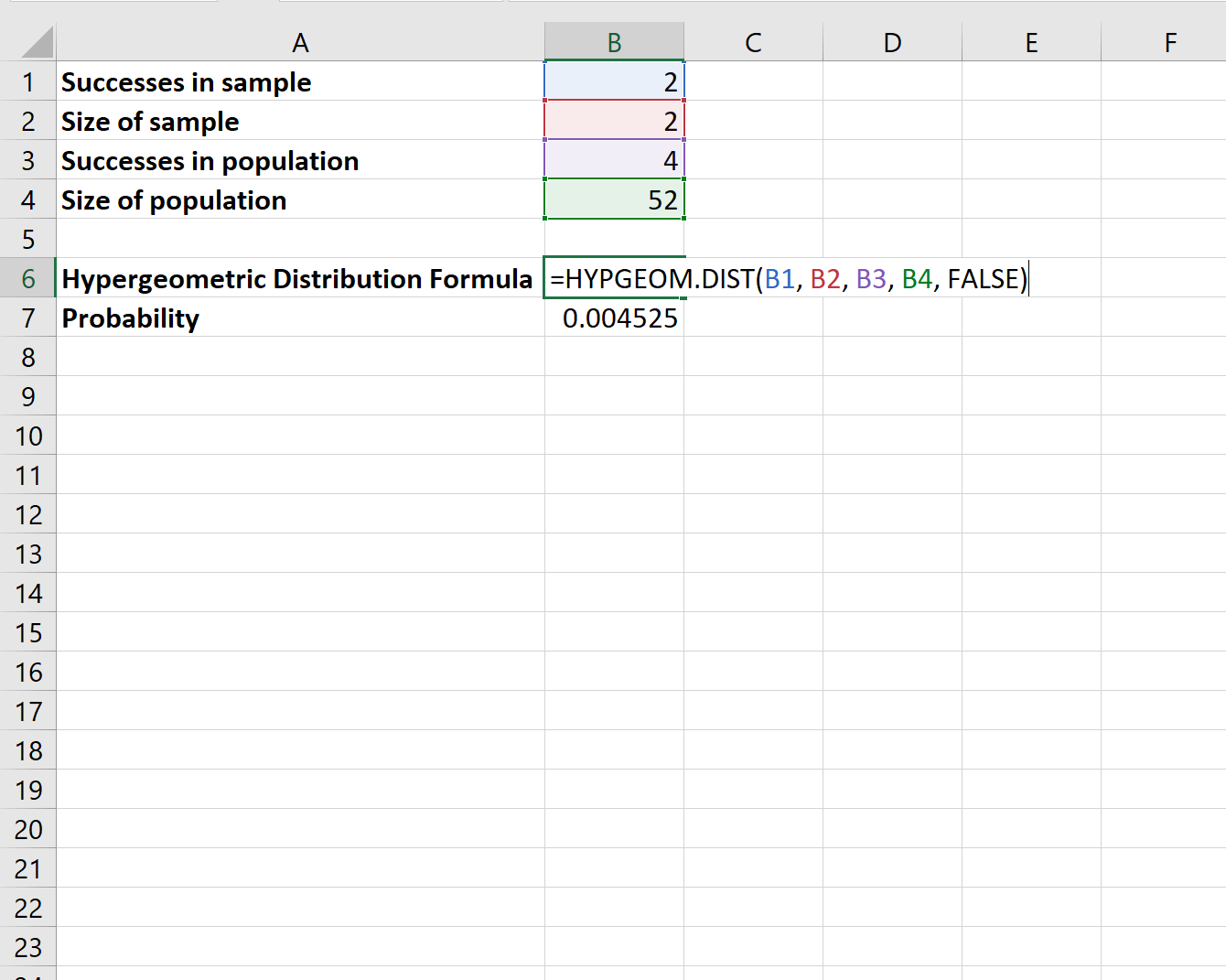
De kans dat beide kaarten Koninginnen zijn, is . 00452 .

Voorbeeld 2: ballen verzamelen uit een urn

In een urn zitten 3 rode ballen en 5 groene ballen. Je kiest willekeurig 4 ballen. Hoe groot is de kans dat je precies 2 rode ballen kiest?

We kunnen de volgende formule in Excel gebruiken om deze waarschijnlijkheid te vinden:

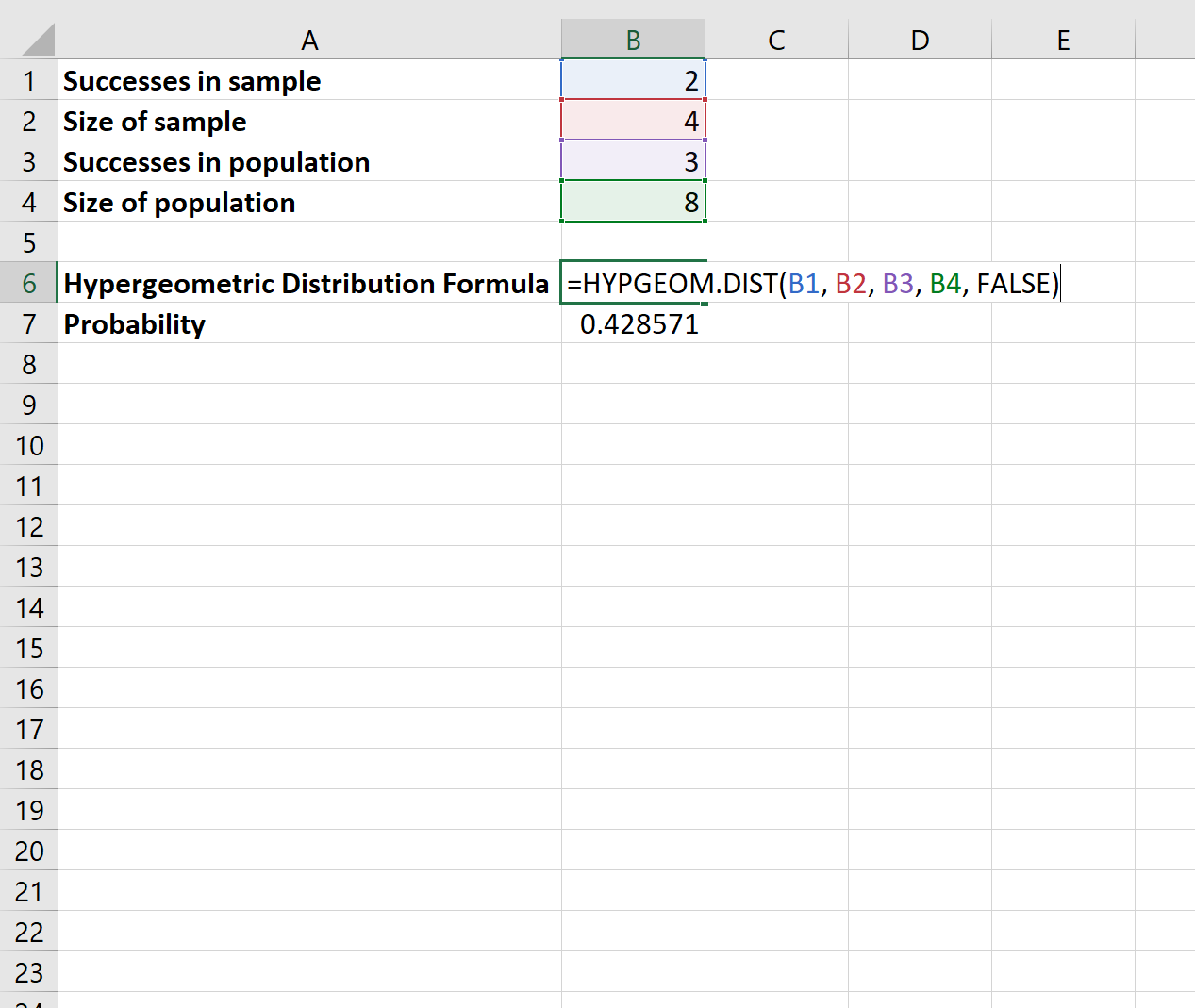
De kans dat je precies 2 rode ballen kiest is . 428571 .

Voorbeeld 3: Knikkers uit een mandje kiezen

In een mandje zitten 7 paarse knikkers en 3 roze knikkers. Je kiest willekeurig 6 knikkers. Hoe groot is de kans dat je precies 3 roze knikkers kiest?

We kunnen de volgende formule in Excel gebruiken om deze waarschijnlijkheid te vinden:

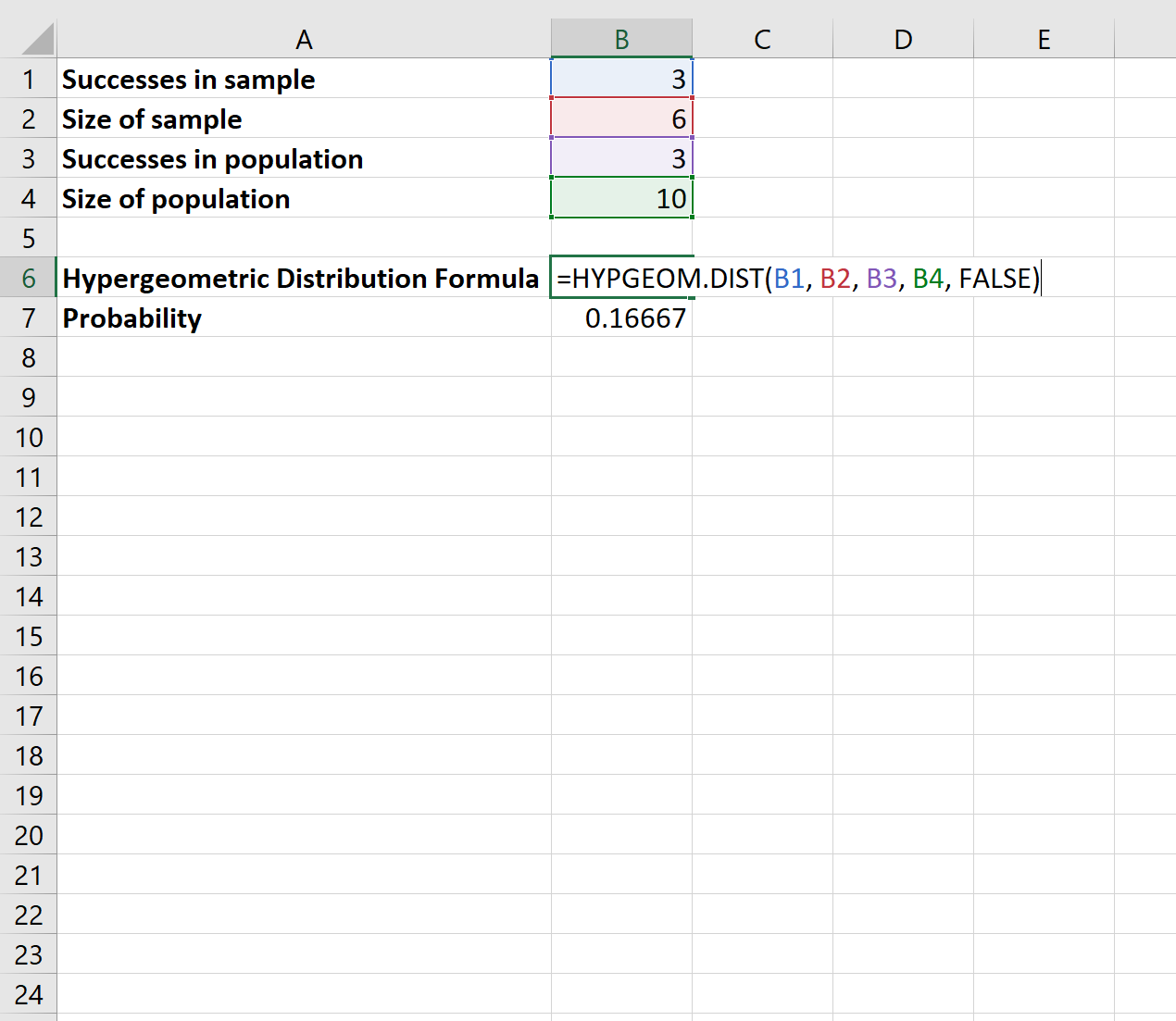
De kans dat je precies 3 roze knikkers kiest is . 16667 .

Aanvullende bronnen

Een inleiding tot de hypergeometrische distributie
Online hypergeometrische distributiecalculator