Hypothesetesten voor het gemiddelde

Von Dr.benjamin anderson August 3, 2023 Statistieken Keine Kommentare

In dit artikel wordt uitgelegd wat het testen van hypothesen voor het gemiddelde in de statistiek is. Zo vindt u de hypothesetestformule voor het gemiddelde en bovendien een oefening die stap voor stap wordt opgelost.

Wat is het testen van hypothesen voor het gemiddelde?

Hypothesetesten voor het gemiddelde zijn een statistische methode die wordt gebruikt om de nulhypothese van een populatiegemiddelde te verwerpen of te verwerpen.

Meer specifiek omvat het testen van hypothesen voor het gemiddelde het berekenen van de teststatistiek en het vergelijken ervan met de kritische waarde om de nulhypothese al dan niet te verwerpen.

Opgemerkt moet worden dat hypothesetests verschillende namen hebben; in de statistiek worden ze ook wel hypothesecontrasten, hypothesetests of significantietests genoemd.

Hypothesetestformule voor gemiddelde

Vervolgens zullen we zien hoe de hypotheseteststatistiek voor het gemiddelde wordt berekend. De formule varieert echter enigszins, afhankelijk van of de variantie bekend is of niet, dus we zullen eerst zien hoe dit wordt gedaan wanneer de variantie bekend is en vervolgens wanneer de variantie onbekend is.

Met bekende afwijking

De testhypotheseformule voor het gemiddelde met bekende variantie is:

$\displaystyle Z=\frac{\overline{x}-\mu}{\displaystyle \frac{\sigma}{\sqrt{n}}}$

Goud:

$Z$

is de hypotheseteststatistiek voor het gemiddelde.
$\overline{x}$

is het steekproefgemiddelde.
$\mu$

is de gemiddelde voorgestelde waarde.
$\sigma$

is de standaarddeviatie van de populatie.
$n$

is de steekproefomvang.

Zodra de hypotheseteststatistiek voor het gemiddelde is berekend, moet het resultaat worden geïnterpreteerd om de nulhypothese te verwerpen of te verwerpen:

Als de hypothesetest voor het gemiddelde tweezijdig is, wordt de nulhypothese verworpen als de absolute waarde van de statistiek groter is dan de kritische waarde Z _α/2 .
Als de hypothesetest voor het gemiddelde overeenkomt met de rechterstaart, wordt de nulhypothese verworpen als de statistiek groter is dan de kritische waarde Z _α .
Als de hypothesetest voor het gemiddelde overeenkomt met de linkerstaart, wordt de nulhypothese verworpen als de statistiek kleiner is dan de kritische waarde -Z _α .

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}$

In dit geval worden de kritische waarden verkregen uit de gestandaardiseerde normale verdelingstabel .

Met onbekende variantie

De testhypotheseformule voor het gemiddelde met onbekende variantie is:

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

Goud:

$t$

is de hypotheseteststatistiek voor het gemiddelde, dat wordt gedefinieerd door een Student’s t-verdeling .
$\overline{x}$

is het steekproefgemiddelde.
$\mu$

is de gemiddelde voorgestelde waarde.
$s$

is de standaardafwijking van het monster.
$n$

is de steekproefomvang.

Net als voorheen moet het berekende resultaat van de teststatistiek worden geïnterpreteerd met de kritische waarde om de nulhypothese al dan niet te verwerpen:

Als de hypothesetest voor het gemiddelde tweezijdig is, wordt de nulhypothese verworpen als de absolute waarde van de statistiek groter is dan de kritische waarde t _α/2|n-1 .
Als de hypothesetest voor het gemiddelde overeenkomt met de rechterstaart, wordt de nulhypothese verworpen als de statistiek groter is dan de kritische waarde t _α|n-1 .
Als de hypothesetest voor het gemiddelde overeenkomt met de linkerstaart, wordt de nulhypothese verworpen als de statistiek kleiner is dan de kritische waarde -t _α|n-1 .

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}$

Wanneer de variantie onbekend is, worden de kritische testwaarden verkregen uit de verdelingstabel van de student.

Voorbeeld uit de praktijk van het testen van hypothesen voor het gemiddelde

Om het concept van het testen van hypothesen voor het populatiegemiddelde volledig te begrijpen, kunt u hieronder een praktijkvoorbeeld van dit soort hypothesetesten bekijken.

Een technologiebedrijf beweert dat de batterij van de laptop die het verkoopt 6 uur meegaat. We controleren of deze hypothese onwaar is door een hypothesetoets uit te voeren met een significantieniveau α = 0,05. Om dit te doen, wordt besloten om 20 eenheden aan te schaffen en de levensduur van de batterij van elke computer te observeren (waarden worden uitgedrukt in uren):

5,2 5,9 7,1 4,2 6,5
8,5 4,6 6,8 6,9 5,8
5,1 6,5 7,0 5,3 6,2
5,7 6,6 7,5 5,1 6,1

In dit geval zijn de nul- en alternatieve hypothesen van de hypothesetest over het gemiddelde als volgt:

$\begin{cases}H_0: \mu=6\\[2ex] H_1:\mu\neq 6 \end{cases}$

Om de teststatistiek te bepalen, moeten we eerst het steekproefgemiddelde en de steekproefstandaarddeviatie berekenen:

$\overline{x}=6,13 \qquad s=1,05$

Omdat we de populatievariantie niet kennen, moeten we, om de teststatistiek te verkrijgen, de hypothesetestformule toepassen voor het gemiddelde met onbekende variantie:

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

$\displaystyle t=\frac{6,13-6}{\displaystyle \frac{1,05}{\sqrt{20}}}$

$\displaystyle t=0,68$

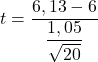
Nu moeten we de kritische waarde van de hypothesetest vinden, dus zoeken we in de Student’s t-verdelingstabel naar de overeenkomstige waarde. De vrijheidsgraden van Student’s t zijn één minder dan de steekproefomvang (20-1=19) en aan de andere kant is de overeenkomstige waarschijnlijkheid de helft van het significantieniveau (0,05/2= 0,025), aangezien het een tweezijdige benadering is. hypothese testen.

$\alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 19}=2,093\end{array}$

Concluderend: aangezien dit een tweezijdige hypothesetest is en de absolute waarde van de teststatistiek kleiner is dan de kritische waarde, wordt de nulhypothese niet verworpen, maar wordt de alternatieve hypothese verworpen.

$0,68<2,093 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Se rechaza } H_1$

Hypothesetesten voor verschil in gemiddelden

De verschil-in-gemiddelden-hypothesetest wordt gebruikt om de nulhypothese dat de gemiddelden van twee populaties hetzelfde zijn, te verwerpen of te accepteren.

De nulhypothese van een hypothesetest voor het verschil tussen twee gemiddelden is dus altijd de volgende:

$H_0: \mu_1=\mu_2$

Hoewel de alternatieve hypothese een van de volgende drie kan zijn:

$\begin{array}{l}H_1:\mu_1\neq \mu_2\\[2ex]H_1:\mu_1>\mu_2\\[2ex]H_1:\mu_1<\mu_2\end{array}$

Vervolgens is de formule om de hypotheseteststatistiek voor het verschil in gemiddelden te berekenen wanneer de variantie bekend is :

$\displaystyle Z=\frac{\displaystyle \overline{x_1}-\overline{x_2}}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

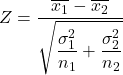
Goud:

$Z$

is de hypotheseteststatistiek voor het verschil tussen twee gemiddelden met bekende variantie, die een standaard normale verdeling volgt.
$\overline{x_1}$

is het gemiddelde van monster 1.
$\overline{x_2}$

is het gemiddelde van monster 2.
$\sigma_1^2$

is de variantie van populatie 1.
$\sigma_2^2$

is de variantie van populatie 2.
$n_1$

is steekproefomvang 1.
$n_2$

is steekproefomvang 2.

Aan de andere kant is de formule voor het berekenen van de hypotheseteststatistiek voor het verschil in gemiddelden wanneer de variantie onbekend is als volgt:

$\displaystyle t=\frac{\displaystyle \overline{x_1}-\overline{x_2}}{\displaystyle\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

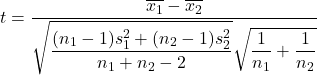
Goud:

$t$

is de hypotheseteststatistiek voor het verschil tussen twee gemiddelden met onbekende variantie, die de Student’s t-verdeling volgt.
$\overline{x_1}$

is het gemiddelde van monster 1.
$\overline{x_2}$

is het gemiddelde van monster 2.
$s_1^2$

is de variantie van monster 1.
$s_2^2$

is de variantie van monster 2.
$n_1$

is steekproefomvang 1.
$n_2$

is steekproefomvang 2.

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder

Wat is het testen van hypothesen voor het gemiddelde?

Hypothesetestformule voor gemiddelde

Met bekende afwijking

Met onbekende variantie

Voorbeeld uit de praktijk van het testen van hypothesen voor het gemiddelde

Hypothesetesten voor verschil in gemiddelden

Über den Autor

Dr.benjamin anderson

Einen Kommentar hinzufügen