Hypothese testen op proportie
In dit artikel wordt uitgelegd wat de proportie van het testen van hypothesen in de statistiek is. Je vindt daarom de formule voor de hypothesetest voor de verhouding en daarnaast een stapsgewijze oefening om volledig te begrijpen hoe het werkt.
Wat is het testen van hypothesen voor proportie?
Het testen van proportiehypothesen is een statistische methode die wordt gebruikt om te bepalen of de nulhypothese van een populatieaandeel al dan niet moet worden verworpen.
Afhankelijk van de waarde van de hypotheseteststatistiek voor de proportie en het significantieniveau wordt de nulhypothese dus verworpen of geaccepteerd.
Merk op dat het testen van hypothesen ook hypothesecontrasten, hypothesetesten of significantietesten kan worden genoemd.
Hypothesetestformule voor verhoudingen
De hypotheseteststatistiek voor de proportie is gelijk aan het verschil in de steekproefproportie minus de voorgestelde waarde van de proportie gedeeld door de standaarddeviatie van de proportie.
De testhypotheseformule voor de verhouding is daarom:

Goud:
-

is de hypotheseteststatistiek voor de proportie.
-

is de steekproefaandeel.
-

is de waarde van het voorgestelde aandeel.
-

is de steekproefomvang.
-

is de standaardafwijking van de verhouding.
Houd er rekening mee dat het niet voldoende is om de hypotheseteststatistiek voor het aandeel te berekenen, maar dat het resultaat vervolgens moet worden geïnterpreteerd:
- Als de hypothesetest voor de proportie tweezijdig is, wordt de nulhypothese verworpen als de absolute waarde van de statistiek groter is dan de kritische waarde Z α/2 .
- Als de hypothesetest voor de verhouding overeenkomt met de rechterstaart, wordt de nulhypothese verworpen als de statistiek groter is dan de kritische waarde Z α .
- Als de hypothesetest voor het aandeel overeenkomt met de linkerstaart, wordt de nulhypothese verworpen als de statistiek kleiner is dan de kritische waarde -Z α .
![Rendered by QuickLaTeX.com \begin{array}{l}H_1: p\neq p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: p> p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: p< p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-7d5bd583532769e3014286e8ffd94c9f_l3.png)
Houd er rekening mee dat kritische waarden eenvoudig kunnen worden verkregen uit de normale verdelingstabel.
Voorbeeld van het testen van hypothesen op evenredigheid
Zodra we de definitie van het testen van hypothesen op proportie zien en wat de formule ervan is, zullen we een voorbeeld oplossen om het concept beter te begrijpen.
- Volgens de fabrikant is een medicijn tegen een specifieke ziekte voor 70% effectief. In het laboratorium testen we de effectiviteit van dit medicijn, omdat onderzoekers denken dat de verhouding anders is. Hiervoor wordt het medicijn getest op een steekproef van 1.000 patiënten en worden 641 mensen genezen. Voer een hypothesetest uit op het populatieaandeel met een significantieniveau van 5% om de hypothese van de onderzoekers al dan niet te verwerpen.
In dit geval zijn de nulhypothese en de alternatieve hypothese van de hypothesetest voor het populatieaandeel:
![Rendered by QuickLaTeX.com \begin{cases}H_0: p=0,70\\[2ex] H_1:p\neq 0,70 \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-f7da8281eeecc022e2ec7daea6a9756e_l3.png)
Het percentage mensen in de steekproef dat door het medicijn is genezen, is:
![]()
We berekenen de hypotheseteststatistiek voor de verhouding door de bovenstaande formule toe te passen:
![Rendered by QuickLaTeX.com \begin{aligned} \displaystyle Z&=\frac{\widehat{p}-p}{\displaystyle\sqrt{\frac{p(1-p)}{n}}}\\[2ex]Z&=\frac{0,641-0,70}{\displaystyle\sqrt{\frac{0,70\cdot (1-0,70)}{1000}}} \\[2ex] Z&=-4,07\end{aligned}}](https://statorials.org/wp-content/ql-cache/quicklatex.com-e689388b0a73e91c1e3d8812c2c4c42a_l3.png)
Aan de andere kant, aangezien het significantieniveau 0,05 is en dit een tweezijdige hypothesetest is, is de kritische waarde van de test 1,96.
![]()
Concluderend is de absolute waarde van de teststatistiek groter dan de kritische waarde, dus verwerpen we de nulhypothese en accepteren we de alternatieve hypothese.
Hypothesetesten voor twee steekproefverhoudingen
Hypothesetesten voor de verhoudingen van twee steekproeven worden gebruikt om de nulhypothese dat de verhoudingen van twee verschillende populaties gelijk zijn, te verwerpen of te accepteren.
De nulhypothese van een hypothesetest voor verhoudingen van twee steekproeven is dus altijd:
![]()
Hoewel de alternatieve hypothese een van de volgende drie opties kan zijn:
*** QuickLaTeX cannot compile formula:
\begin{array}{l}H_1:p_1\neq p_2\\[2ex]H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio of the two samples is calculated as follows:[latex]p=\cfrac {x_1+x_2}{n_1+n_2}
*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ...H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio
Please use \mathaccent for accents in math mode.
leading text: ...\[2ex]H_1:p_1 The combined ratio of the two
Please use \mathaccent for accents in math mode.
leading text: ...combined of the two samples is calculated
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
En de formule om de hypotheseteststatistiek voor twee steekproefverhoudingen te berekenen is:
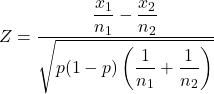
Goud:
-

is de hypotheseteststatistiek voor verhoudingen van twee steekproeven.
-
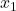
is het aantal resultaten in monster 1.
-
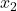
is het aantal resultaten in monster 2.
-

is steekproefomvang 1.
-

is steekproefomvang 2.
-

is het gecombineerde aandeel van de twee monsters.
Hypothesetesten voor k-monsterverhoudingen
Bij een hypothesetest over de verhoudingen van k steekproeven is het doel om te bepalen of alle verhoudingen van de verschillende populaties gelijk zijn of, integendeel, of er verschillende verhoudingen zijn. Daarom zijn de nulhypothese en de alternatieve hypothese in dit geval:
![Rendered by QuickLaTeX.com \begin{cases}H_0: \text{Todas las proporciones son iguales}\\[2ex] H_1: \text{No todas las proporciones son iguales} \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-77d7e13b427dd927953473a6bfbe9a55_l3.png)
In dit geval wordt het gecombineerde aandeel van alle monsters als volgt berekend:
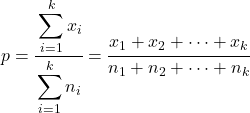
De formule voor het vinden van de hypotheseteststatistiek voor k-steekproefverhoudingen is:
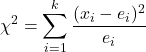
![]()
Goud:
-

is de hypotheseteststatistiek voor k steekproefverhoudingen. In dit geval volgt de statistiek een chikwadraatverdeling.
-

is het aantal resultaten in monster i.
-

is de steekproefomvang i.
-

is het gecombineerde aandeel van alle monsters.
-

is het aantal hits dat wordt verwacht van voorbeeld i. Het wordt berekend door het gecombineerde aandeel te vermenigvuldigen

op steekproefomvang

.