Hypothesetesten voor variantie

Von Dr.benjamin anderson August 3, 2023 Statistieken Keine Kommentare

In dit artikel wordt uitgelegd wat het testen van hypothesen op variantie is. Je vindt dus de formule voor het testen van variantiehypothesen en bovendien een oefening die stap voor stap wordt opgelost.

Wat is hypothesetesten voor variantie?

Hypothesetesten op variantie is een statistische methode die wordt gebruikt om te bepalen of de nulhypothese van een populatievariantie al dan niet moet worden verworpen. Met andere woorden, het testen van variantiehypothesen wordt gebruikt om de hypothese over de waarde van de variantie van een populatie te verwerpen of te accepteren.

Specifiek wordt, afhankelijk van de waarde van de hypotheseteststatistiek voor variantie en het gekozen significantieniveau, de nulhypothese verworpen of geaccepteerd.

Houd er rekening mee dat het testen van hypothesen vele namen heeft. Het kan ook hypothesecontrasten, hypothesetesten of significantietesten worden genoemd.

Hypothesetestformule voor variantie

De hypothesetoetsingsstatistiek voor variantie is gelijk aan het verschil tussen de steekproefgrootte minus één keer de steekproefvariantie en gedeeld door de voorgestelde waarde van de populatievariantie. De hypotheseteststatistiek voor variantie heeft een chikwadraatverdeling .

De formule voor het berekenen van de hypotheseteststatistiek voor variantie is dus als volgt:

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

Goud:

$\chi^2$

is de hypotheseteststatistiek voor variantie, die een chikwadraatverdeling heeft.
$n$

is de steekproefomvang.
$s^2$

is de steekproefvariantie.
$\sigma^2$

is de voorgestelde populatievariantie.

Om het resultaat van de statistiek te interpreteren, moet de verkregen waarde worden vergeleken met de kritische waarde van de test.

Als de variantietest van de hypothese tweezijdig is, wordt de nulhypothese verworpen als de statistiek groter is dan de kritische waarde.
$\chi_{1-\alpha/2|n-1}^2$

of als de kritische waarde kleiner is dan

$\chi_{\alpha/2|n-1}$

.
Als de hypothesetest voor de variantie overeenkomt met de rechterstaart, wordt de nulhypothese verworpen als de statistiek groter is dan de kritische waarde
$\chi_{1-\alpha|n-1}^2$

.
Als de hypothesetest voor variantie overeenkomt met de linkerstaart, wordt de nulhypothese verworpen als de statistiek kleiner is dan de kritische waarde
$\chi_{\alpha|n-1}$

.

$\begin{array}{l}H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha/2|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si }\chi^2<\chi^2_{\alpha/2|n-1}\text{ se rechaza } H_0 \\[3ex]H_1: \sigma^2> \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2< \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2<\chi^2_{\alpha|n-1}\text{ se rechaza } H_0\end{array}$

De kritische hypothesetestwaarden voor variantie worden verkregen uit de chikwadraatverdelingstabel. Merk op dat de vrijheidsgraden voor de Chi-kwadraatverdeling de steekproefgrootte minus 1 zijn.

Voorbeeld uit de praktijk van het testen van hypothesen op variantie

Nadat we de definitie van het testen van variantiehypothesen hebben gezien en wat de formule ervan is, zullen we een concreet voorbeeld zien om de assimilatie van het concept te voltooien.

Een fabriek beschikt over een machine die met hoge precisie onderdelen voor een auto produceert. Er wordt echter vermoed dat het bedrijf zich heeft teruggetrokken en nu onderdelen produceert met een tussenruimte groter dan 8 mm ² . Om deze hypothese te weerleggen wordt een monster van 25 stuks geanalyseerd en de steekproefvariantie bedraagt 9,1 mm ² . Kan de initiële hypothese worden verworpen met een significantieniveau α=0,05?

De nulhypothese en alternatieve hypothese voor deze variantiehypothesetest zijn als volgt:

$\begin{cases}H_0: \sigma^2=8 \\[2ex] H_1:\sigma^2>8 \end{cases}“ title=“Rendered by QuickLaTeX.com“ height=“65″ width=“101″ style=“vertical-align: 0px;“> Om te bepalen of de nulhypothese al dan niet kan worden verworpen, berekenen we de hypotheseteststatistiek voor de variantie met behulp van de formule die we hierboven hebben gezien: <p class=$ $\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

$\chi^2=\cfrac{(25-1)\cdot 9,1}{8}$

$\chi^2=27,3$

We zoeken nu naar de kritische waarde die overeenkomt met de rechterstaart voor 24 vrijheidsgraden en een significantieniveau α=0,05 in de Chi-kwadraatverdelingstabel:

$\begin{array}{c}\chi^2_{1-\alpha|n-1}=\ \color{orange}\bm{?}\color{black}\\[2ex]\chi^2_{0,95|24}=36,415\end{array}$

De berekende statistiek is dus kleiner dan de kritische waarde van de test en daarom wordt de nulhypothese van de variantiehypothesetest niet verworpen, maar wordt eerder de alternatieve hypothese verworpen.

$27,3<36,415 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{No se rechaza } H_0$

➤ Zie: Hypothesetesten voor het populatiegemiddelde
➤ Zie: Hypothesetesten voor populatieaandeel

Hypothesetesten voor de variantie van twee populaties

Variantiehypothesetesten met twee populaties worden gebruikt om de hypothese dat de varianties van twee verschillende populaties gelijk zijn, te verwerpen of te accepteren.

De nulhypothese van een hypothesetest over de variantie van twee populaties is dus altijd de volgende:

$H_0: \sigma^2_1=\sigma^2_2$

En de alternatieve hypothese kan een van de volgende drie opties zijn:

$\begin{array}{l}H_1:\sigma^2_1\neq \sigma^2_2\\[2ex]H_1:\sigma^2_1>\sigma^2_2\\[2ex]H_1:\sigma^2_1<\sigma^2_2\end{array}$

In dit geval is de formule voor het berekenen van de hypotheseteststatistiek voor de variantie van twee populaties:

$F=\cfrac{s_1^2}{s_2^2}$

Goud:

$F$

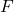
is de hypotheseteststatistiek voor de variantie van twee populaties, die een F-verdeling volgt.
$\sigma_1^2$

is de variantie van populatie 1.
$\sigma_2^2$

is de variantie van populatie 2.
$s_1^2$

is de variantie van monster 1.
$s_2^2$

is de variantie van monster 2.
$n_1$

is steekproefomvang 1.
$n_2$

is steekproefomvang 2.

Omdat de Snedecor F-verdeling niet symmetrisch is, wordt de nulhypothese verworpen op basis van de volgende criteria:

[latex]\begin{array}{l}H_1: \sigma_1^2\neq \sigma_2^2 \ \color{oranje}\bm{\longrightarrow}\color{zwart} \ \text{Si } F>F_{ 1-\alpha/2|n_1-1|n_2-1}\text{ zie } H_0\\[3ex]H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow }\color{zwart} \ \text{If }F \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{If } F>F_{1-\alpha|n_1-1|n_2-1}\text{ zie rechaza } H_0\\[3ex]H_1: \sigma_1^2< \sigma_2^2 \ \color{oranje}\bm{\longrightarrow}\color{zwart} \ \text{Si } F

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder