Instrumentele variabelen: definitie en voorbeelden

Vaak proberen we in de statistiek het effect van de ene variabele op de andere te schatten. We willen bijvoorbeeld graag weten:

• Welke invloed heeft de tijd die je besteedt aan studeren op de examenscores?
• Hoe beïnvloedt een bepaald medicijn de bloeddruk?
• Hoe beïnvloedt stress de hartslag?

In elk scenario willen we begrijpen of een voorspellende variabele al dan niet een responsvariabele beïnvloedt. Er zijn echter vaak andere variabelen die de relatie tussen de twee variabelen beïnvloeden.

Stel dat we bijvoorbeeld een bepaald medicijn gebruiken als voorspellende variabele en bloeddruk als responsvariabele. We zijn alleen geïnteresseerd in het effect van het medicijn op de bloeddruk:

Andere variabelen, zoals de tijd die aan lichaamsbeweging wordt besteed, het algemene dieet en het stressniveau, hebben echter ook invloed op de bloeddruk:

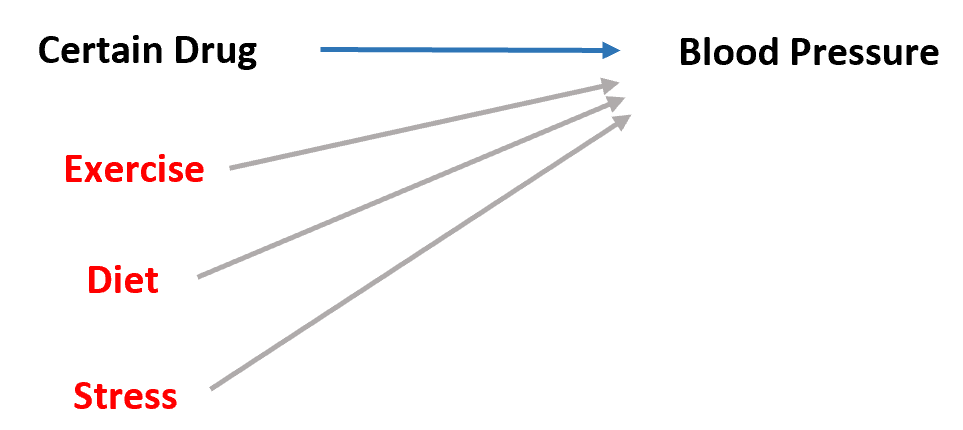
Als we dus eeneenvoudige lineaire regressie uitvoeren met het medicijn als voorspellende variabele en de bloeddruk als responsvariabele, kunnen we er niet zeker van zijn dat de regressiecoëfficiënten het effect van het medicijn op de bloeddruk nauwkeurig zullen weergeven, omdat externe factoren (lichaamsbeweging, dieet, stress, enz.) kunnen ook een rol spelen.

Een mogelijke manier om dit probleem te omzeilen is het gebruik van een instrumentele variabele .

Wat is een instrumentele variabele?

Een instrumentele variabele is een derde variabele die in de regressieanalyse wordt geïntroduceerd en die gecorreleerd is met de voorspellende variabele, maar niet gecorreleerd is met de responsvariabele. Met behulp van deze variabele wordt het mogelijk om het werkelijke causale effect te schatten dat een voorspellende variabele heeft op een responsvariabele.

Stel dat we bijvoorbeeld het effect van een bepaald medicijn op de bloeddruk willen schatten:

Een voorbeeld van een instrumentele variabele die we in deze regressieanalyse kunnen gebruiken, is de nabijheid van een individu tot een apotheek.

Deze „nabijheids“-variabele zou waarschijnlijk sterk gecorreleerd zijn met het feit of het individu de medicatie in kwestie al dan niet inneemt, aangezien een individu het überhaupt niet zou kunnen verkrijgen als hij niet in de buurt van een apotheek woont.

De variabele ‘nabijheid’ mag echter geen enkele correlatie hebben met de bloeddruk. De enige associatie die het zou hebben met de bloeddruk is via de voorspellende variabele.

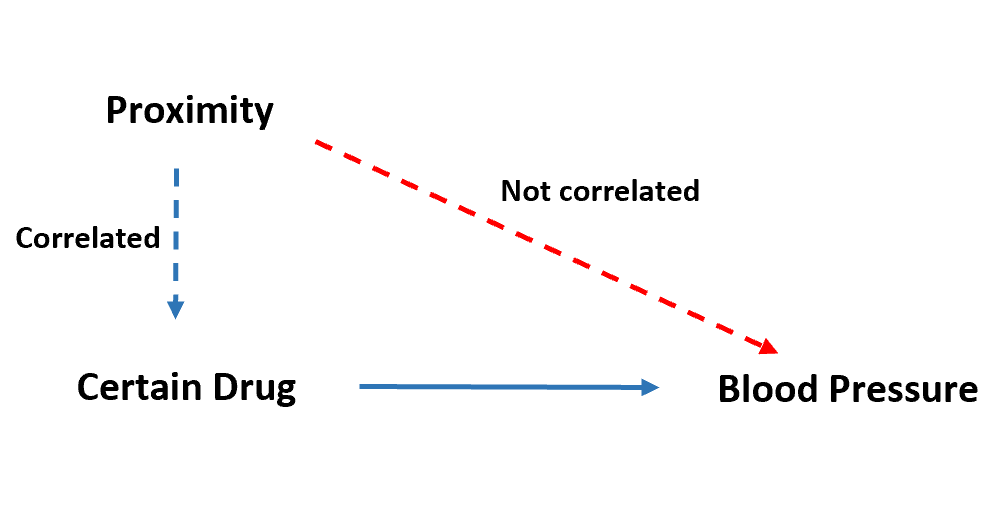
De manier waarop we een instrumentele variabele feitelijk gebruiken, is door instrumentele variabelenregressie uit te voeren, ook wel tweetraps kleinste kwadratenregressie genoemd.

Instrumentele variabelenregressie

Bij instrumentele variabelenregressie (of regressie in twee fasen met de kleinste kwadraten) wordt de volgende benadering gebruikt om het effect van een voorspellende variabele op een responsvariabele te schatten:

Stap 1: Pas een regressiemodel toe met de instrumentele variabele als voorspellende variabele.

In ons specifieke voorbeeld zouden we eerst het volgende regressiemodel passen:

Bepaalde medicijnen = B ₀ + B ₁ (nabijheid)

We zouden dan de voorspelde waarden voor bepaalde medicijnen (cd) overhouden, die we cd _hat zullen noemen.

Stap 2: Pas een tweede regressiemodel toe met behulp van de voorspelde waarden voor cd _hat .

Vervolgens passen we het volgende regressiemodel toe:

Bloeddruk = B ₀ + B ₁ (cd- _hoed )

Als de regressiecoëfficiënt van cd _hat statistisch significant blijkt te zijn, kunnen we zeggen dat er een causaal effect van het medicijn op de bloeddruk is.

De reden dat we dit kunnen zeggen is omdat we alleen de term ’nabijheid‘ hebben gebruikt om CD _Hat te creëren en we weten dat nabijheid niet gecorreleerd mag zijn met de bloeddruk; elke significante correlatie in de tweede fase van regressie kan worden toegeschreven aan een bepaald medicijn.

Voorzorgsmaatregelen met betrekking tot het gebruik van instrumentele variabelen

Een instrumentele variabele mag alleen worden gebruikt als deze aan de volgende criteria voldoet:

• Het is sterk gecorreleerd met de voorspellende variabele.
• Het is niet gecorreleerd met de responsvariabele.
• Het is niet gecorreleerd met andere variabelen die uit het model zijn uitgesloten (nabijheid is bijvoorbeeld niet gecorreleerd met lichaamsbeweging, voeding of stress).

Als een instrumentele variabele niet aan dit criterium voldoet, mag deze niet in het regressiemodel worden gebruikt, omdat deze waarschijnlijk onbetrouwbare en vertekende resultaten zal opleveren.