Interkwartielbereik (of interkwartielbereik)

In dit artikel wordt uitgelegd wat de interkwartielafstand, ook wel de interkwartielafstand genoemd, is. U zult ook kunnen zien hoe de interkwartielafstand wordt berekend aan de hand van een concreet voorbeeld. Je leert waar de interkwartielafstand voor is en wat het verschil is met het interval. Bovendien kunt u het interkwartielbereik van elke dataset berekenen met een online rekenmachine.

Wat is het interkwartielbereik (of interkwartielbereik)?

Het interkwartielbereik, ook wel interkwartielbereik genoemd, is een maatstaf voor de statistische spreiding die het verschil tussen het derde en eerste kwartiel aangeeft. Om het interkwartielbereik van een statistische dataset te berekenen, moet u daarom eerst het derde en eerste kwartiel vinden en deze vervolgens aftrekken.

In het kort wordt het interkwartielbereik uitgedrukt door het acroniem IQR.

Een van de meest voordelige kenmerken van de interkwartielafstand is dat het een robuuste statistiek is, dat wil zeggen dat het een hoge robuustheid heeft ten opzichte van uitschieters. Omdat bij de berekening van het interkwartielbereik geen rekening wordt gehouden met extreme waarden, zal de waarde ervan zeer weinig variëren als er nieuwe uitschieters verschijnen.

Uiteraard zijn er naast het interkwartielbereik nog andere spreidingsmaten; de bekendste maatstaven zijn het bereik, de variantie, de standaard (of standaard) deviatie, de gemiddelde afwijking en de variatiecoëfficiënt.

Hoe het interkwartielbereik (of interkwartielbereik) te berekenen

Om in de statistiek het interkwartielbereik (of interkwartielbereik) van een dataset te berekenen, moet je eerst het eerste en derde kwartiel van de dataset vinden en vervolgens de aftrekking van het derde kwartiel minus het eerste kwartiel berekenen.

Daarom is de formule voor het berekenen van de interkwartielafstand of interkwartielafstand:

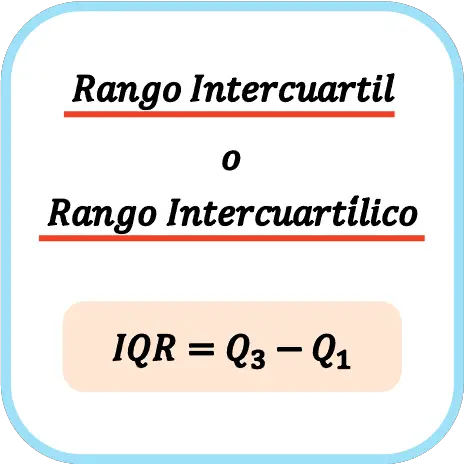
👉 U kunt de onderstaande rekenmachine gebruiken om het interkwartielbereik voor elke dataset te berekenen.

Daarom is het essentieel dat u weet hoe de kwartielen van een statistische steekproef worden berekend. Daarom raad ik u aan voordat u verdergaat het volgende artikel te raadplegen en vervolgens verder te gaan met de uitleg.

Voorbeeld van interkwartiel (of interkwartiel) bereik

Gegeven de definitie en formule voor de interkwartielafstand (of interkwartielafstand), vindt u hieronder een opgeloste oefening, zodat u precies kunt zien hoe dit type spreidingsmaatstaf wordt berekend.

• Wij willen statistisch analyseren of het een goed idee is om in een bedrijf te investeren. Om dit te doen, hebben we gegevens verzameld over de aandelenkoers van dit bedrijf gedurende de afgelopen 15 maanden. In de volgende tabel ziet u de waargenomen gegevens, gerangschikt van laag naar hoog. Bereken het interkwartielbereik voor deze dataset.

Zoals we in de vorige sectie hebben gezien, moeten we, om de interkwartielafstand (of interkwartielafstand) van de steekproef te verkrijgen, eerst het eerste en derde kwartiel berekenen.

Het eerste kwartiel is de mediaan van de eerste helft van de waarden, wat overeenkomt met € 8,95/aandeel.

Aan de andere kant is het derde kwartiel de tussenwaarde van de tweede helft van de waarden, dus € 9,83/aandeel.

Om het interkwartielbereik te vinden, past u eenvoudigweg de formule toe en trekt u het derde kwartiel min het eerste kwartiel af.

Interkwartiel (of interkwartiel) bereikcalculator

Voer een statistische gegevensset in de volgende rekenmachine in om het interkwartielbereik of interkwartielbereik te berekenen. Gegevens moeten worden gescheiden door een spatie en moeten worden ingevoerd met de punt als decimaal scheidingsteken.

Verschil tussen interkwartielbereik en bereik

In de statistieken zijn het verschil tussen het interkwartielbereik (of interkwartielbereik) en het interval de waarden die worden gebruikt om de berekening uit te voeren. Het interkwartielbereik is het verschil tussen het derde en eerste kwartiel, terwijl het bereik het verschil is tussen de extreme waarden van de steekproef.

Het interkwartielbereik meet dus de spreiding van een monster met behulp van de centrale gegevens, terwijl het interval de spreiding van het monster kwantificeert met behulp van de extreme gegevens.

Daarom wordt het statistische bereik veel meer beïnvloed door uitbijters , omdat deze meestal het minimum of maximum van de dataset vertegenwoordigen. Een van de voordelen van het interkwartielbereik over het interval is dus dat het een grotere robuustheid heeft.

Waar wordt het interkwartielbereik voor gebruikt?

In de eerste plaats wordt het interkwartielbereik (of interkwartielbereik) gebruikt om de distributie van een dataset te meten . volledig Hoewel het analyseren van de spreiding van een steekproef het berekenen van meer statistische metingen vereist, geeft het interkwartielbereik een idee van hoe verspreid de steekproef is, althans de centrale waarden.

De interpretatie van de interkwartielafstand is daarom relatief eenvoudig. Hoe hoger de waarde van het interkwartielbereik, hoe meer verspreid de middelste gegevens in de steekproef zijn, en hoe kleiner het interkwartielbereik, hoe dichter de middelste gegevens bij elkaar liggen.

Bovendien is het interkwartielbereik ook nuttig voor het maken van een box-and-whisker-plot, een veelgebruikt diagram voor het analyseren van aandelenkoersgedrag op de aandelenmarkt.