Wordt de interkwartielafstand (iqr) beïnvloed door uitschieters?

In de statistiek willen we vaak weten hoe breed waarden ‘verspreid’ zijn in een verdeling.

Een populaire manier om de spreiding te meten is het interkwartielbereik , dat wordt berekend als het verschil tussen het eerste kwartiel en het derde kwartiel van een dataset. Kwartielen zijn eenvoudigweg waarden die een dataset in vier gelijke delen verdelen.

Voorbeeld: Berekening van het interkwartielbereik

Het volgende voorbeeld laat zien hoe u het interkwartielbereik voor een bepaalde gegevensset kunt berekenen:

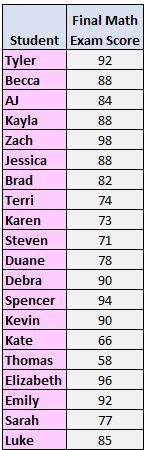
Stap 1: Rangschik de waarden van klein naar groot.

58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

2. Zoek de mediaan.

58, 66, 71, 73, 74, 77 , 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

In dit geval ligt de mediaan tussen 85 en 88.

3. De mediaan verdeelt de dataset in twee helften. De mediaan van de onderste helft is het onderste kwartiel en de mediaan van de bovenste helft is het bovenste kwartiel:

58, 66, 71, 73, 74 , 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

4. Bereken het interkwartielbereik.

In dit geval is het eerste kwartiel het gemiddelde van de middelste twee waarden in de onderste helft van de dataset (75,5) en het derde kwartiel het gemiddelde van de middelste twee waarden in de bovenste helft van de set gegevens (91).

Het interkwartielbereik is dus 91 – 75,5 = 15,5

Het interkwartielbereik wordt niet beïnvloed door uitschieters

Een van de redenen waarom mensen de voorkeur geven aan het gebruik van de interkwartielafstand (IQR) bij het berekenen van de ‘spreiding’ van een dataset, is dat deze robuust is voor uitschieters. Omdat de IQR simpelweg het middelste bereik van 50% van de gegevenswaarden is, wordt deze niet beïnvloed door extreme uitschieters .

Om dit aan te tonen, kunt u de volgende dataset overwegen:

[1, 4, 8, 11, 13, 17, 17, 20]

Hier volgen de verschillende propagatiestatistieken voor deze dataset:

• Interkwartielbereik: 11
• Bereik: 19
• Standaardafwijking: 6,26
• Verschil: 39,23

Beschouw nu dezelfde dataset, maar met een extreme uitschieter toegevoegd:

[1, 4, 8, 11, 13, 17, 17, 20, 150 ]

Hier volgen de verschillende propagatiestatistieken voor deze dataset:

• Interkwartielafstand: 12,5
• Bereik: 149
• Standaardafwijking: 43,96
• Spreiding: 1.932,84

Merk op dat de interkwartielafstand slechts licht verandert, van 11 naar 12,5. Alle andere spreidingsmaatstaven veranderen echter dramatisch.

Dit toont aan dat het interkwartielbereik niet wordt beïnvloed door uitschieters zoals andere spreidingsmaatstaven. Om deze reden is het een betrouwbare manier om de verdeling van de middelste 50% van de waarden in elke verdeling te meten.

Verder lezen:

Verspreidingsmetingen
Interkwartielafstandscalculator