Interpolatie of extrapolatie: wat is het verschil?

Twee termen die studenten vaak verwarren in de statistiek zijn interpolatie en extrapolatie .

Hier is het verschil:

Interpolatie verwijst naar het voorspellen van waarden die binnen een bereik van datapunten vallen.

Extrapolatie verwijst naar het voorspellen van waarden die buiten een bereik van datapunten vallen.

Het volgende voorbeeld illustreert het verschil tussen de twee termen.

Voorbeeld: interpolatie en extrapolatie

Stel dat we de volgende dataset hebben:

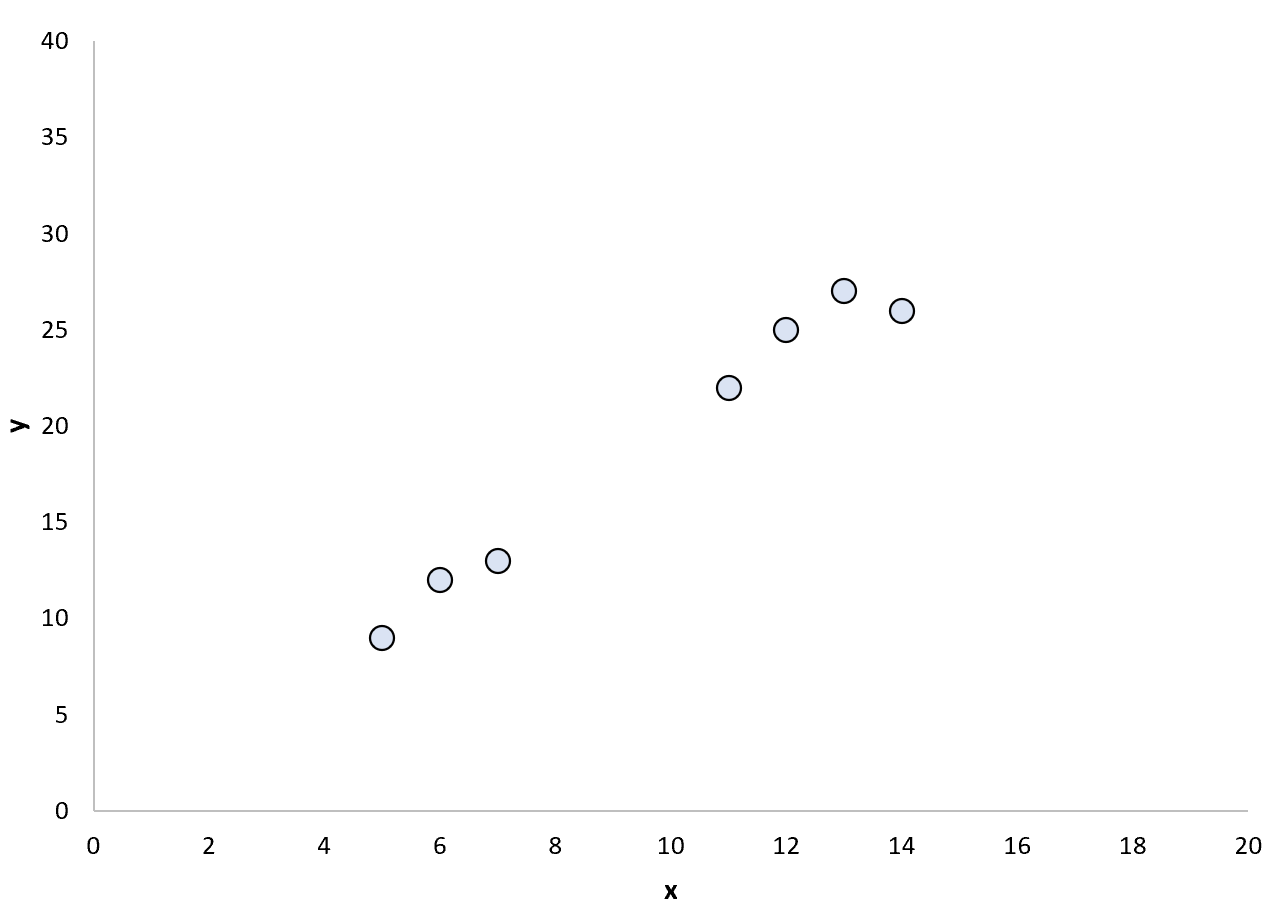
We kunnen besluiten om een eenvoudig lineair regressiemodel op deze punten toe te passen:

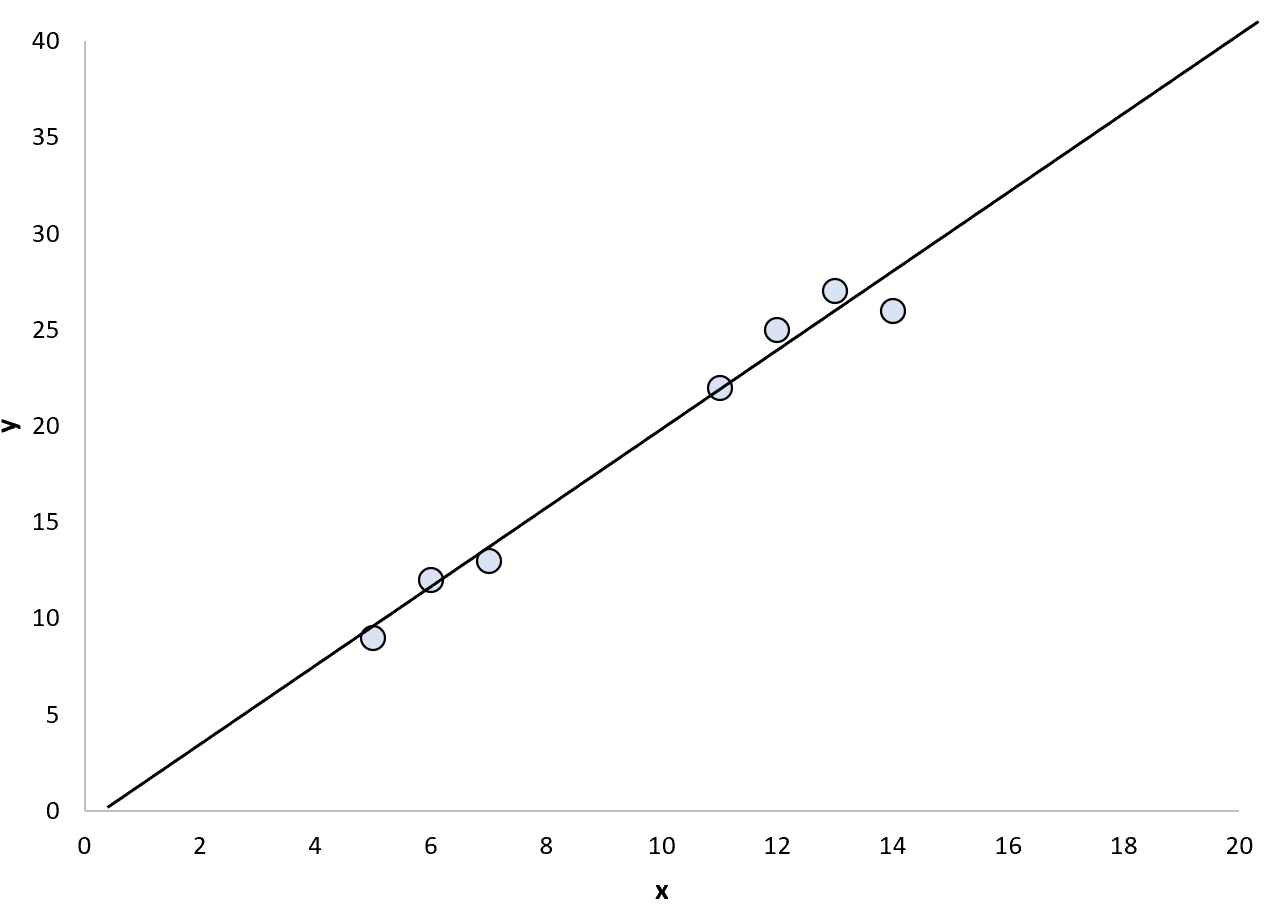
We zouden dan het gepaste regressiemodel kunnen gebruiken om puntwaarden zowel binnen als buiten het bereik van datapunten te voorspellen.

Wanneer we het gepaste regressiemodel gebruiken om de puntwaarden binnen het bestaande bereik van datapunten te voorspellen, wordt dit interpolatie genoemd.

Omgekeerd, wanneer we het gepaste regressiemodel gebruiken om puntwaarden buiten het bestaande bereik te voorspellen, wordt dit extrapolatie genoemd:

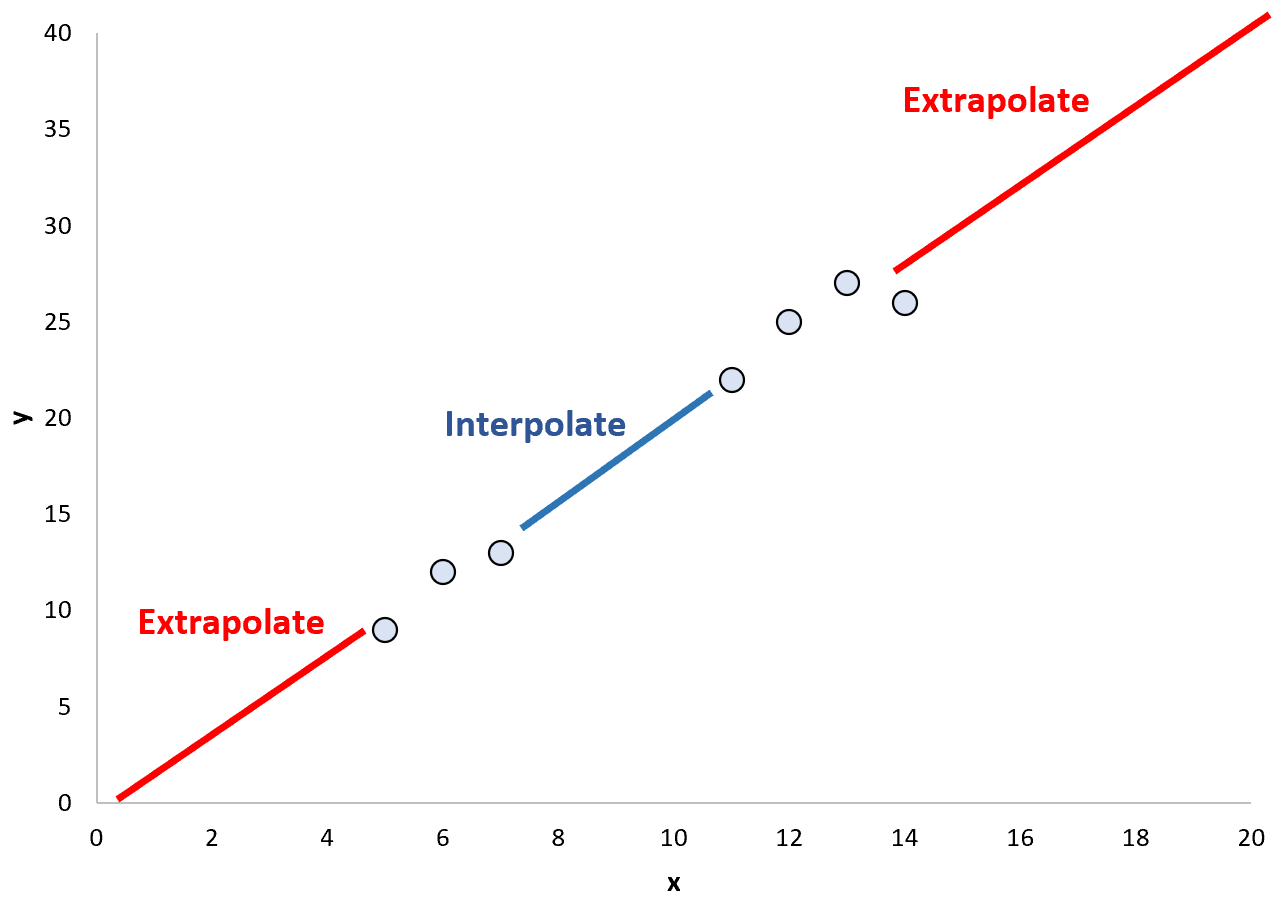
Het potentiële gevaar van extrapolatie

Wanneer we extrapoleren, gaan we ervan uit dat hetzelfde patroon dat binnen het huidige bereik van gegevenspunten bestaat, ook buiten het bereik bestaat.

Dit kan echter een gevaarlijke veronderstelling zijn, omdat het mogelijk is dat het patroon dat buiten het huidige bereik van gegevenspunten bestaat, heel anders is:

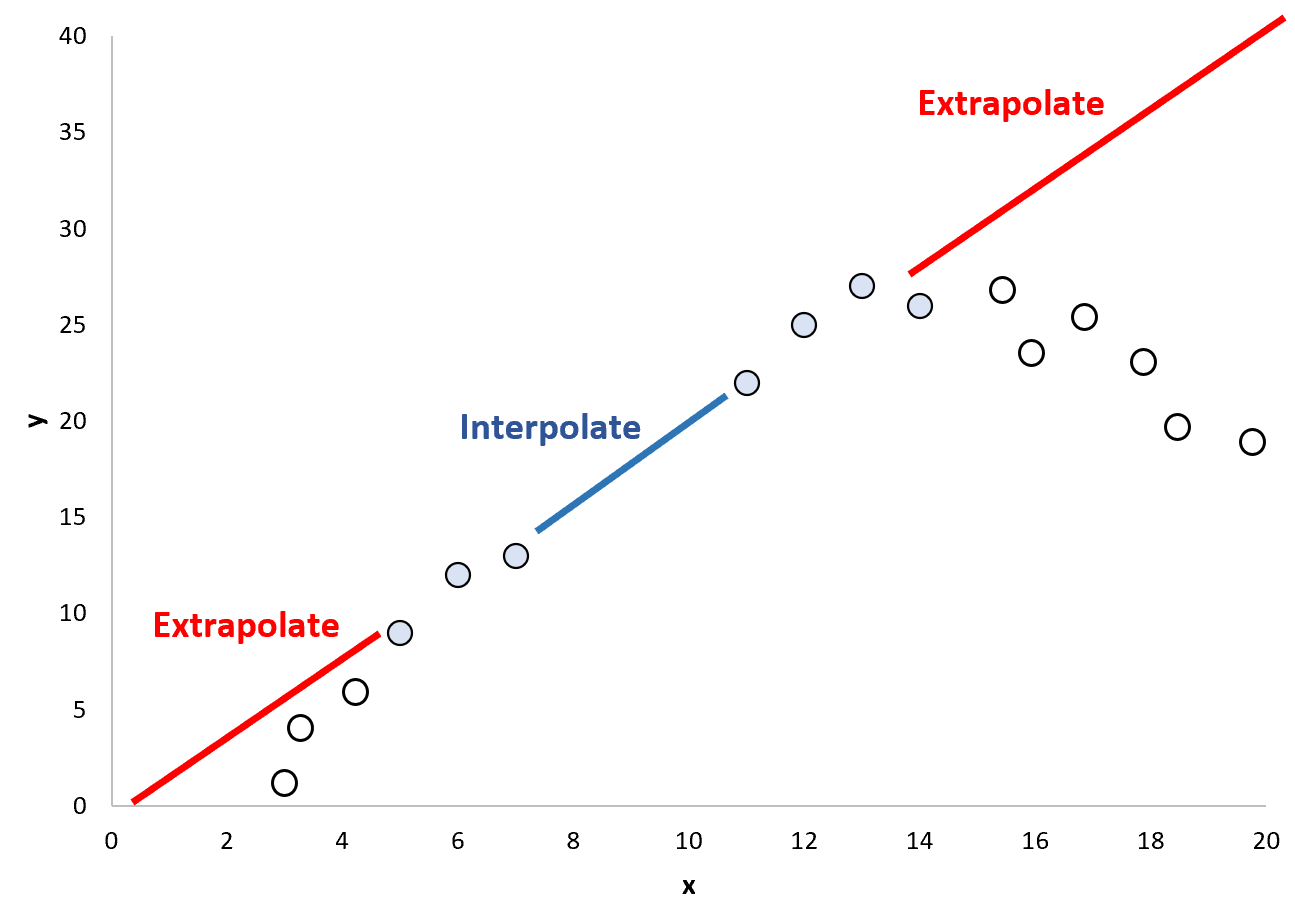
Om deze reden kan het gevaarlijk zijn om extrapolatie te gebruiken om datapuntwaarden te voorspellen die buiten het bereik van waarden vallen die zijn gebruikt om het regressiemodel te maken.

In de praktijk is het vaak zinvol om extrapolatie te gebruiken om puntwaarden te voorspellen die iets buiten het bereik van bestaande waarden vallen, maar hoe verder je van het bereik af gaat, hoe waarschijnlijker het is dat het verschil tussen de voorspelde waarde en de werkelijke waarde waarde is belangrijk. .

Wanneer extrapolatie gebruiken?

Vaak is er domeinspecifieke expertise nodig om te bepalen of extrapolatie een redelijk idee is of niet.

Stel bijvoorbeeld dat een marketingafdeling van een bedrijf een eenvoudig lineair regressiemodel toepast, waarbij de advertentie-uitgaven als voorspellende variabele en de totale omzet als responsvariabele worden gebruikt.

In dit scenario kan het redelijk zijn om aan te nemen dat een gestage stijging van de advertentie-uitgaven zal resulteren in een voorspelbare stijging van de totale inkomsten:

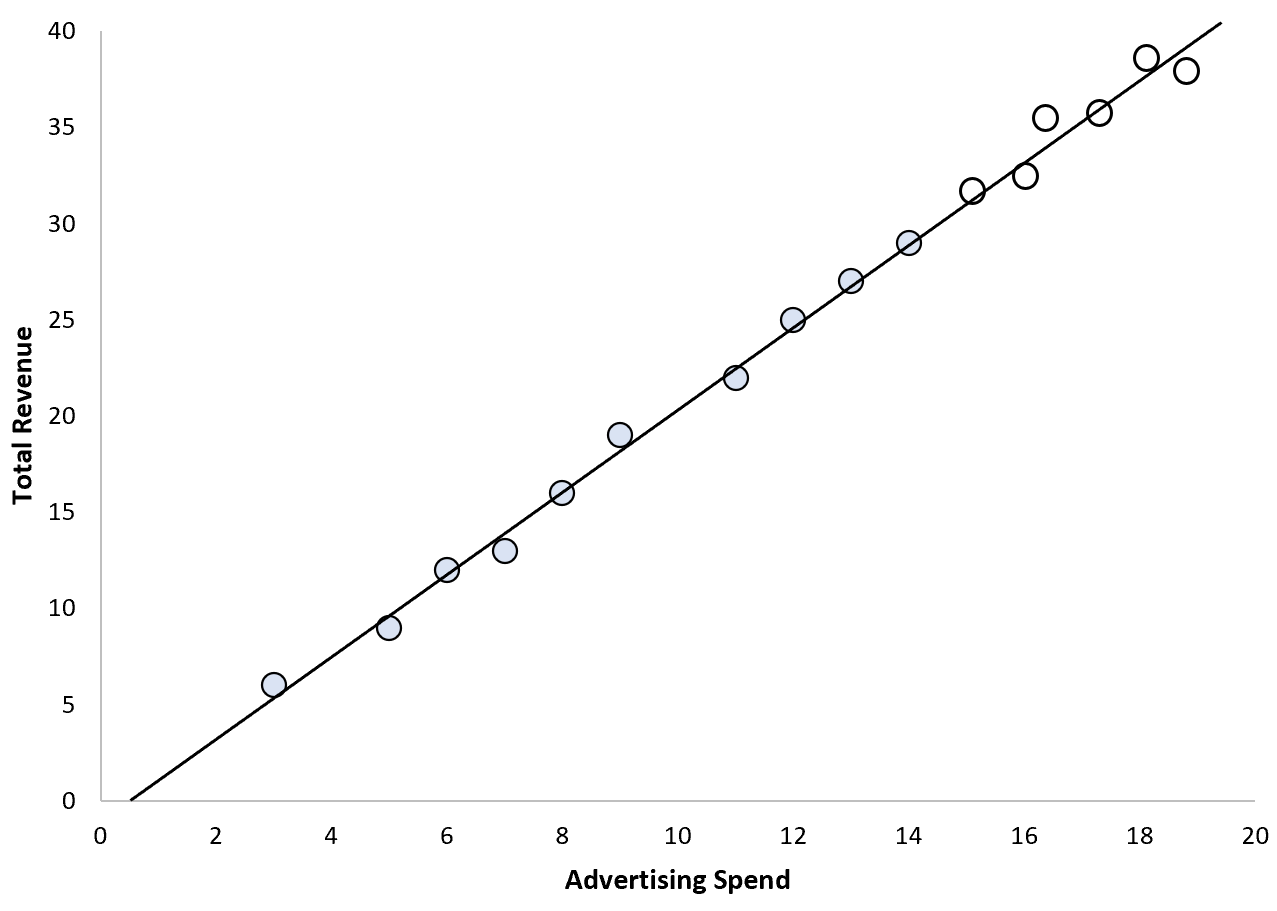
In dit scenario kunnen we er vrij zeker van zijn dat we waarden kunnen extrapoleren.

Neem echter een scenario waarin een bioloog totale kunstmest wil gebruiken om de plantengroei te voorspellen.

Ze besluit misschien om een eenvoudig lineair regressiemodel op de gegevenspunten toe te passen, maar aangezien er een bovengrens is aan de planthoogte, heeft het waarschijnlijk geen zin om extrapolatie te gebruiken om de puntwaarden te voorspellen. buiten het waardebereik. waarden gebruikt om in het model te passen:

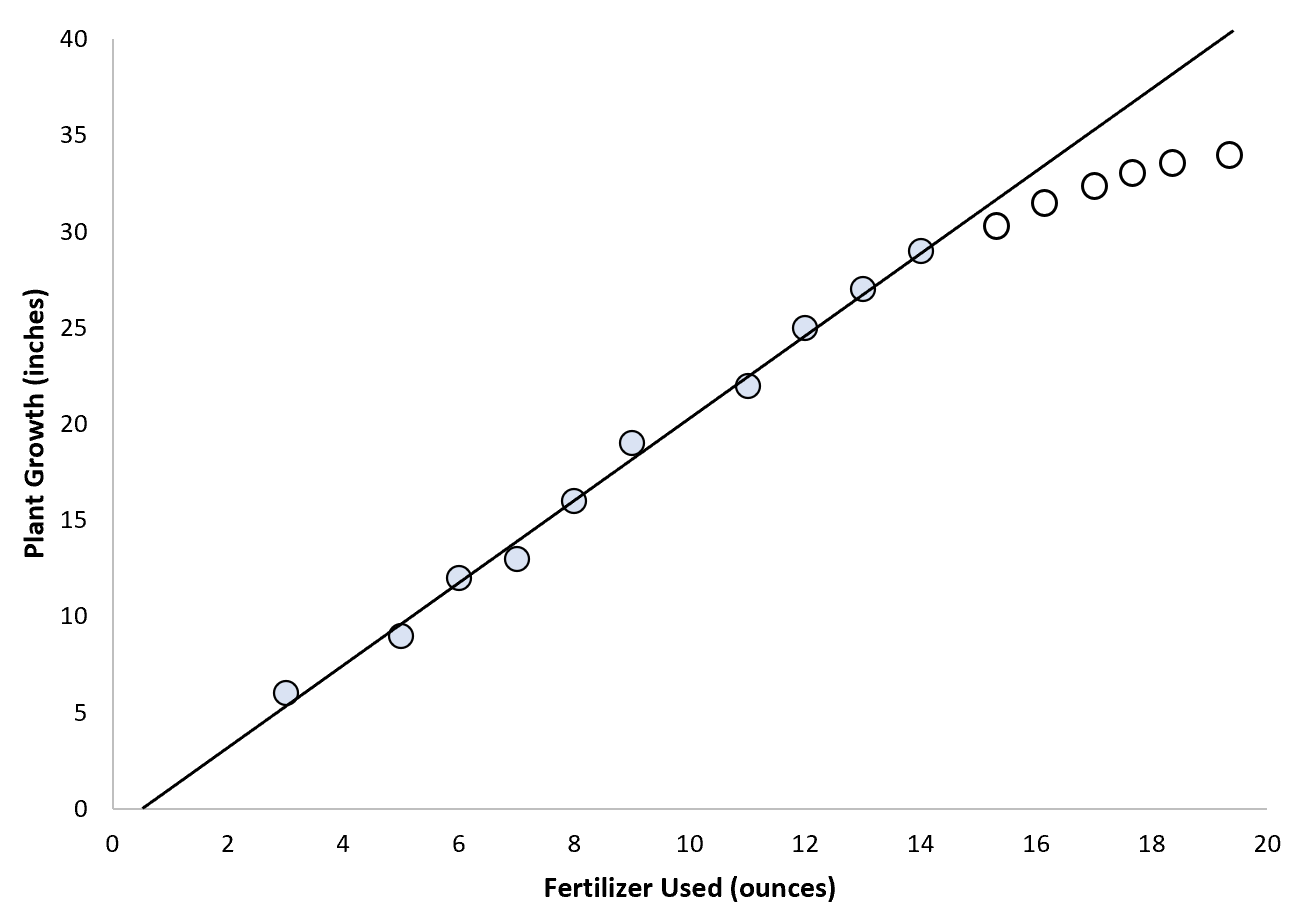
In dit scenario hebben we mogelijk veel minder vertrouwen in ons vermogen om waarden te extrapoleren.

De conclusie : extrapolatie kan op sommige gebieden zinvoller zijn dan op andere, maar er bestaat altijd een potentieel gevaar dat het model dat bestaat binnen het bereik van waarden dat wordt gebruikt om in het model te passen, niet buiten het strand bestaat.

Aanvullende bronnen

Lineaire interpolatie uitvoeren in Excel
Hoe voorspellingen te doen met lineaire regressie